山西省太原市2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-11-01 类型:期末考试
一、单选题
-
1. -2的绝对值是()
A、2 B、 C、 D、-22. 下列调查中,适宜采用抽样调查的是( )A、调查一批从疫情中高风险地区来并人员的核酸检测结果 B、调查奥运会马拉松比赛运动员兴奋剂的使用情况 C、调查某批中性笔的使用寿命 D、调查神舟十三号载人飞船各零部件的质量3. 如图所示的几何体是由5个完全相同的小正方体搭成的,从它的左面看得到的平面图形是( ) A、
A、 B、
B、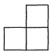 C、
C、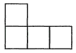 D、
D、 4. 下列运算结果正确的是( )A、3a+2b=5ab B、 C、 D、5. 如图所示的网格是正方形网格,则∠AOB与∠MPN的关系是( )
4. 下列运算结果正确的是( )A、3a+2b=5ab B、 C、 D、5. 如图所示的网格是正方形网格,则∠AOB与∠MPN的关系是( )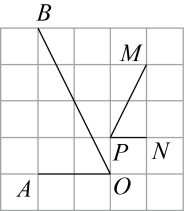 A、∠AOB>∠MPN B、∠AOB<∠MPN C、∠AOB=∠MPN D、∠AOB=2∠MPN6. 近年来,国家持续加大对铁路行业尤其是对高速铁路的投资力度,《中长期铁路网规划》提出,到2025年,铁路网规模达到17.5万公里左右,其中高速铁路3.8万公里左右,数据3.8万公里用科学记数法表示为( )
A、∠AOB>∠MPN B、∠AOB<∠MPN C、∠AOB=∠MPN D、∠AOB=2∠MPN6. 近年来,国家持续加大对铁路行业尤其是对高速铁路的投资力度,《中长期铁路网规划》提出,到2025年,铁路网规模达到17.5万公里左右,其中高速铁路3.8万公里左右,数据3.8万公里用科学记数法表示为( ) A、米 B、米 C、米 D、米7. 根据下列语句画相应的几何图形,正确的是( )A、
A、米 B、米 C、米 D、米7. 根据下列语句画相应的几何图形,正确的是( )A、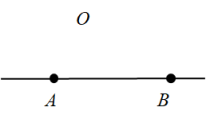 点O在直线AB上
B、
点O在直线AB上
B、 直线AB与CD都经过点O
C、
直线AB与CD都经过点O
C、 在∠ABC内部画射线BP
D、
在∠ABC内部画射线BP
D、 延长BA到点C,使BC=2AB
8. 如图是一张边长为5cm的正方形纸片,将其四个角都减去一个边长为xcm的正方形,沿虚线折成一个无盖的长方体盒子,这个盒子的容积(单位:)为( )
延长BA到点C,使BC=2AB
8. 如图是一张边长为5cm的正方形纸片,将其四个角都减去一个边长为xcm的正方形,沿虚线折成一个无盖的长方体盒子,这个盒子的容积(单位:)为( ) A、 B、 C、 D、9. “鸡兔同笼”是中国古代数学名题之一,记载于《孙子算经》之中,叙述为“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”其意思为“若干只鸡兔同在一个笼子里,从上面数,有35个头,从下面数,有94只脚.问笼中鸡和兔各有多少只?”若设鸡有x只,则x满足的方程为( )
A、 B、 C、 D、9. “鸡兔同笼”是中国古代数学名题之一,记载于《孙子算经》之中,叙述为“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”其意思为“若干只鸡兔同在一个笼子里,从上面数,有35个头,从下面数,有94只脚.问笼中鸡和兔各有多少只?”若设鸡有x只,则x满足的方程为( ) A、2x+4(35-x)=94 B、4x+2(35-x)=94 C、x+35-x=35 D、94-2x=35-x10. 移动5G通信网络将推动我国数字经济发展迈上新台阶.据预测,2020年到2025年中国5G直接经济产出和间接经济产出的情况如图所示,根据图中提供的信息,下列推断错误的是( )
A、2x+4(35-x)=94 B、4x+2(35-x)=94 C、x+35-x=35 D、94-2x=35-x10. 移动5G通信网络将推动我国数字经济发展迈上新台阶.据预测,2020年到2025年中国5G直接经济产出和间接经济产出的情况如图所示,根据图中提供的信息,下列推断错误的是( ) A、2020年到2025年,5G间接经济产出和直接经济产出都呈增长趋势 B、2022年,5G间接经济产出是直接经济产出的2倍 C、2024年到2025年,5G间接经济产出和直接经济产出的增长率相同 D、2025年,5G间接经济产出比直接经济产出多3万亿元
A、2020年到2025年,5G间接经济产出和直接经济产出都呈增长趋势 B、2022年,5G间接经济产出是直接经济产出的2倍 C、2024年到2025年,5G间接经济产出和直接经济产出的增长率相同 D、2025年,5G间接经济产出比直接经济产出多3万亿元二、填空题
-
11. 计算-1-2的结果是 .12. 如图,射线OC平分∠AOB, , 则∠AOC的度数为 .
 13. 观察下列等式:
13. 观察下列等式:, , , ⋯
第1个等式 第2个等式 第3个等式⋯
按此规律,则第n个等式为 .
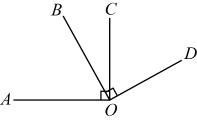
14. 苏女士在某微商服务平台经营服装销售,一款服装的进价为300元/件,若她想按标价的八折销售,仍可获利20%,则这款服装的标价应为元/件.15. 如图,∠AOC=∠BOD=90°,OB在∠AOC的内部,OC在∠BOD的内部,OE是∠AOB的一条三等分线.请从A,B两题中任选一题作答.A.当∠BOC=30°时,∠EOD的度数为 .
B.当∠BOC=α°时,∠EOD的度数为(用含α的代数式表示).
三、解答题
-
16. 计算或求值:(1)、;(2)、化简并求值: , 其中x=3,y=-1.17. 解下列方程:(1)、5x-2=2x+1;(2)、3-x=2+5(x-1).18. 下面是小乐同学解一元一次方程的过程,请认真阅读并解答问题.
解方程 .
解:去分母,得6x-(x+2)=8.……第一步
去括号,得6x-x-2=8.……第二步
移项,得6x-x=-8+2.…第三步
合并同类项,得5x=-6,……第四步
方程两边同除以5,得 . …第五步
(1)、以上求解过程中,第一步的依据是;(2)、从第步开始出现错误,具体的错误是;(3)、该方程正确的解为 .19. 如图,已知不在同一直线上的三点A,B,C. (1)、按下面的要求用尺规作图:连接AB,AC,作射线BC;在射线BC上取一点D,使CD=AB.(2)、用刻度尺在(1)的图中画出BC的中点M.若BC=6,AB=8,求MD的长.20. 第24届冬季奥林匹克运动会,即2022年北京冬季奥运会,将于2022年2月4日开幕,共设7个大项,15个分项,109个小项.学校从七年级同学中随机抽取若干名,组织了奥运知识竞答活动,将他们的成绩进行整理,得到如下不完整的频数分布表、频数分布直方图与扇形统计图.(满分为100分,将抽取的成绩分成A,B,C,D四组,每组含最大值不含最小值)
(1)、按下面的要求用尺规作图:连接AB,AC,作射线BC;在射线BC上取一点D,使CD=AB.(2)、用刻度尺在(1)的图中画出BC的中点M.若BC=6,AB=8,求MD的长.20. 第24届冬季奥林匹克运动会,即2022年北京冬季奥运会,将于2022年2月4日开幕,共设7个大项,15个分项,109个小项.学校从七年级同学中随机抽取若干名,组织了奥运知识竞答活动,将他们的成绩进行整理,得到如下不完整的频数分布表、频数分布直方图与扇形统计图.(满分为100分,将抽取的成绩分成A,B,C,D四组,每组含最大值不含最小值)分组
频数
A:60~70
4
B:70~80
12
C:80~90
16
D:90~100
△
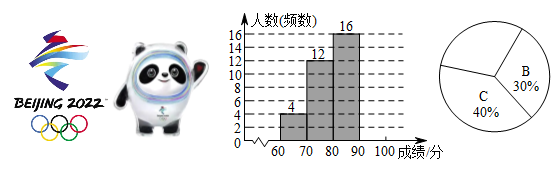 (1)、本次知识竞答共抽取七年级同学名,D组成绩在扇形统计图中对应的圆心角为°;(2)、请将频数分布直方图与扇形统计图补充完整;(3)、学校将此次竞答活动的D组成绩记为优秀,已知该校初、高中共有学生2400名,小敏想根据七年级竞答活动的结果,估计全校学生中奥运知识掌握情况达到优秀等级的人数.请你判断她这样估计是否合理并说明理由.21. 2021年9月19日,太原城中“远去”的钟声,今又响起,随着钟楼街上钟楼的复建,承载着一代代太原人记忆的这条老街,经过17个月的修整,盛装迎客.小亮和同学在钟楼街的一家店铺购买了2杯奶茶和3杯橙汁,一共花了29元,已知一杯奶茶比一杯橙汁贵2元,求奶茶和橙汁的单价.
(1)、本次知识竞答共抽取七年级同学名,D组成绩在扇形统计图中对应的圆心角为°;(2)、请将频数分布直方图与扇形统计图补充完整;(3)、学校将此次竞答活动的D组成绩记为优秀,已知该校初、高中共有学生2400名,小敏想根据七年级竞答活动的结果,估计全校学生中奥运知识掌握情况达到优秀等级的人数.请你判断她这样估计是否合理并说明理由.21. 2021年9月19日,太原城中“远去”的钟声,今又响起,随着钟楼街上钟楼的复建,承载着一代代太原人记忆的这条老街,经过17个月的修整,盛装迎客.小亮和同学在钟楼街的一家店铺购买了2杯奶茶和3杯橙汁,一共花了29元,已知一杯奶茶比一杯橙汁贵2元,求奶茶和橙汁的单价. 22. 阅读材料,解答下列问题:
22. 阅读材料,解答下列问题:幻方历史悠久,传说最早出现在夏禹时代的“洛书”(如图1)把图1的洛书用今天的数学符号翻译出来,就是一个三阶幻方,如图2,它的每行、每列、每条对角线上的三个数的和都和等.

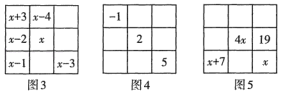 (1)、在图2中,每行、每列、每条对角线上三个数的和为;(2)、设图3所示的三阶幻方中间的数为x(x为整数),请用含x的代数式将图3幻方补充完整;(3)、从A,B两题中任选一题作答.我选择 ▲ 题.
(1)、在图2中,每行、每列、每条对角线上三个数的和为;(2)、设图3所示的三阶幻方中间的数为x(x为整数),请用含x的代数式将图3幻方补充完整;(3)、从A,B两题中任选一题作答.我选择 ▲ 题.A.将-2,-1,0,1,2,3,4,5,6这9个数中除-1,2,5外的6个数填入图4中其余的方格中,使其成为一个三阶幻方.
B.如图5是一个三阶幻方,按方格中已给的信息,x的值为 ▲ , 4x上方的方格中的数为 ▲ .
23. 问题情境:太原市已建成的汾河健身智慧步道,从长风桥到胜利桥共8000米,步道上铺有保护膝盖的松软塑胶,吸引了广大市民前来健身,周日,小明和小亮相约去该步道建身,如图,小明从步道的长风桥端(记为点A)出发向胜利桥端(记为点B)方向行走,速度为150米/分,同时小亮从距离A点500米处的步道上一点C出发向点B行走,速度为100米/分,设他们行走的时间为x分钟.请解答下列问题.
数学思考:
(1)、在上述行走过程中,小明离开A点的距离为米,小亮离A点的距离为米(均用含x的式子表示);(2)、求小明追上小亮时x的值;(3)、请从A,B两题中任选一题作答.我选择 ▲ 题.如图,步道上点E处是一个出口,它到起点A的距离为3500米.因有其他事情,小明到达E点后立即按原速度返回,到C点停止行走;小亮到达E点也停止了行走.
A.求小明返回途中与小亮相距250米时x的值.
B.求小明返回途中与小亮之间的距离恰好是小亮到点E距离的一半时x的值.