山西省吕梁市孝义市2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-11-01 类型:期末考试
一、单选题
-
1. 如图是2021年12月28日山西太原的天气预报图,这天山西太原的气温为﹣15~4℃,太原这天的最高气温与量低气温的温差是( )
 A、19℃ B、11℃ C、﹣11℃ D、﹣19℃2. 下列是同类项的是( )A、2x和2y B、和 C、和 D、和3. 若a=b,则下列不一定成立的是( )A、 B、 C、 D、4. 如图是一个三棱柱,从正面看到的图形是( )
A、19℃ B、11℃ C、﹣11℃ D、﹣19℃2. 下列是同类项的是( )A、2x和2y B、和 C、和 D、和3. 若a=b,则下列不一定成立的是( )A、 B、 C、 D、4. 如图是一个三棱柱,从正面看到的图形是( )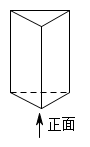 A、
A、 B、
B、 C、
C、 D、
D、 5. 有理数a,b在数轴上的对应点的位置如图所示,则下列结论正确的是( )
5. 有理数a,b在数轴上的对应点的位置如图所示,则下列结论正确的是( ) A、 B、 C、 D、6. 下列选项正确的是( )A、 B、 C、 D、7. 解方程 , 步骤如下:
A、 B、 C、 D、6. 下列选项正确的是( )A、 B、 C、 D、7. 解方程 , 步骤如下:去括号,得 第一步
移项,得 第二步
合并同类项,得 第三步
系数化为1,得 第四步
以上解方程步骤中,开始出现错误的是( )
A、第一步 B、第二步 C、第三步 D、第四步8. 今年10月孝义市遭受洪灾,汛情发生后,我市及时启动防汛应急抢险预案,加固河道堤防,某河段需要18台挖土、运土机械,每台机械每小时能挖土或运土 , 为了使挖上和运土工作同时开始,同时结束,安排了x台机械被挖土,则可列方程( )A、 B、 C、 D、9. 如图,下列表述错误的是( ) A、线段AB和射线AC都是直线AB的一部分 B、点D在直线AB上 C、直线AC和直线BD相交于点B D、直线BD不经过点A10. 周末,奶奶买了一些小桔子,小亮、姐姐、弟弟做了一个有趣的游戏:首先姐姐,小亮,弟弟手中拿上相同数量的桔子(每人手中的桔子大于4个),然后依次完成以下步骤:
A、线段AB和射线AC都是直线AB的一部分 B、点D在直线AB上 C、直线AC和直线BD相交于点B D、直线BD不经过点A10. 周末,奶奶买了一些小桔子,小亮、姐姐、弟弟做了一个有趣的游戏:首先姐姐,小亮,弟弟手中拿上相同数量的桔子(每人手中的桔子大于4个),然后依次完成以下步骤:第一步:姐姐给小亮2个桔子;
第二步:弟弟给小亮1个桔子;
第三步:此时,姐姐手中有几个桔子,小亮就给姐姐几个桔子.
请你确定,最终小亮手中剩余的桔子有几个( )
A、3 B、4 C、5 D、6二、填空题
-
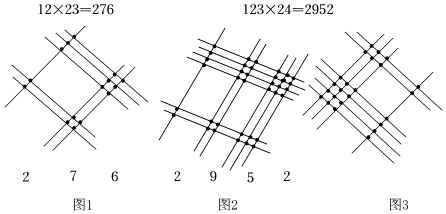
11. 我国粮食产量连续7年保持在1.3万亿斤以上,有力保障了14亿人口大国的粮食安全.1.3万亿斤用科学记数法表示为斤.12. 已知∠A=32°15′48″,则∠A余角的度数为(用度分秒形式表示)13. 有理数的乘法运算,除了用乘法口诀外,现有一种“划线法”:如图1,表示的乘法算式是12×23=276;图2表示的是123×24=2952.则图3表示的乘法算式是 .
 14. 一件商品进价是a元,按进价提高40%标价,再打8折出售,那么每件商品的售价为元.(含a的式子表示)15. 中国始有历法大约在四千年前.每页显示一日信息的叫日历,每页显示一个月信息的叫月历,每页显示全年信息的叫年历,如图是2022年1月份的月历,用一个方框按图中所示的方式(阴影部分)圈出任意的4个数,若这四个数的和是84.设方框左上角的数是x,则可列方程 .
14. 一件商品进价是a元,按进价提高40%标价,再打8折出售,那么每件商品的售价为元.(含a的式子表示)15. 中国始有历法大约在四千年前.每页显示一日信息的叫日历,每页显示一个月信息的叫月历,每页显示全年信息的叫年历,如图是2022年1月份的月历,用一个方框按图中所示的方式(阴影部分)圈出任意的4个数,若这四个数的和是84.设方框左上角的数是x,则可列方程 .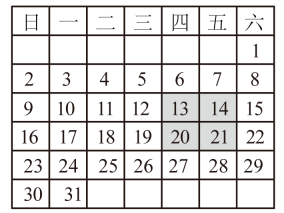
三、解答题
-
16. 计算(1)、(2)、17. 先化简再求值:2(3x2y-xy2)-3(x2y-2xy2),其中x=-1,y=-2.18. 解方程:19. 如图1是墨水瓶包装盒实物图,图2是粉笔包装盒实物图,图3是墨水瓶包装盒展开图,图4是粉笔包装盒展开图,尺寸数据如下(单位:cm.以下问题结果用含a,b,c的式子表示,其中阴影部分为内部粘贴角料,计算纸片面积时内部粘贴角料忽略不计):
 (1)、做一个墨水瓶包装盒需要纸片的面积为 , 做一个粉笔包装盒需要纸片的面积为;(直接写出答案)(2)、做一个墨水瓶包装盒和一个粉笔包装盒共用纸片多少平方厘米?(3)、做三个粉笔包装盒比做两个墨水瓶包装盒多用多少平方厘米纸片?20. 如图,已知线段a,b,射线AM.
(1)、做一个墨水瓶包装盒需要纸片的面积为 , 做一个粉笔包装盒需要纸片的面积为;(直接写出答案)(2)、做一个墨水瓶包装盒和一个粉笔包装盒共用纸片多少平方厘米?(3)、做三个粉笔包装盒比做两个墨水瓶包装盒多用多少平方厘米纸片?20. 如图,已知线段a,b,射线AM.实践与操作:在射线AM上作线段AB=a,AC=a-b.(要求:尺规作图,保留作图痕迹,不写作法)

推理与探究:若线段AB的中点是点D,线段BC的中点是点E,请在上图中标出点D,E.探究:线段DE与AC有怎样的数量关系,并说明理由.
21. 阅读下列材料,完成相应任务.学习了一元一次方程之后,数学兴趣小组了解到如下信息:
我国的铁路旅客列车,按不同的进行速度、运行范围、设备配置、作业特征等,分为不同的级别,列车的级别由车次开头的字母来表示(部分是纯数字).如G字头,表示高速动车组旅客列车;D字动,表示动车组旅客列车;C字头,表示城际旅客列车;K学头,表示快速旅客列年,等等.随着交通的发展吕梁站至太原南站已并通了多次列车,其中“C150”次列车的平均速度是120km/h,“K1334”次列车的平均速度是90km/h,并且“C150”次列车从吕梁站至太原南站所时间比“K1334”次列车少用30分钟(两列车中途停留时间均除外).
兴趣小组提出了以下两个问题:
(1)、“C150”次列车和“K1334”次列车从吕梁站至太原南站所用时同分别是多少?(2)、吕梁站至太原南站的路程为多少km?小彬列的方程是“”
任务一:①小彬同学所列方程中的x表示 ▲ ,
②小彬同学列方程所用的数量关系为 ▲ (“路程÷速度=时间“除外);
任务二:小亮的做法是:设“K1334”次列车从吕梁站至太原南站所用时间为y小时,请你帮助小亮解决上述两个问题,写出解答过程.
22. 综合与探究数学活动课上,老师提出如下问题:如图1,将含30°的三角尺COD的直角顶点O放在直线AB上,三角尺COD中,∠COD=90°,∠C=60°,∠D=30°.过点O作射线OE.

 (1)、∠AOC的补角是 , ∠COE的余角是;(直接写回答案)(2)、如图2,“启航”小组根据学习几何积累的活动经验:特殊的位置可以得到特殊的结论,在图1的基础上继续展开探究,他们提出的问题是:调整三角尺的位置,当OD平分∠BOE时,OC平分∠AOE.请你证明启航小组提出的问题;(3)、如图3,受到“启航”小组的启发,“睿智”小组提出的问题是:在图2的基础上,继续调整三角尺的位置,当OE平分∠BOC时,∠AOC与∠DOE有怎样的数量关系?请说明理由.
(1)、∠AOC的补角是 , ∠COE的余角是;(直接写回答案)(2)、如图2,“启航”小组根据学习几何积累的活动经验:特殊的位置可以得到特殊的结论,在图1的基础上继续展开探究,他们提出的问题是:调整三角尺的位置,当OD平分∠BOE时,OC平分∠AOE.请你证明启航小组提出的问题;(3)、如图3,受到“启航”小组的启发,“睿智”小组提出的问题是:在图2的基础上,继续调整三角尺的位置,当OE平分∠BOC时,∠AOC与∠DOE有怎样的数量关系?请说明理由.