山西省临汾市霍州市2021-2022学年上学期七年级期末数学试题
试卷更新日期:2022-11-01 类型:期末考试
一、单选题
-
1. 2022的相反数是( )A、2022 B、-2022 C、 D、±20222. 2021年末寒潮来袭,全国各地气温骤降.如图表示2022年元月某天山西省四个城市的最低气温情况.这一天最低气温最高的城市为( )
城市
太原
大同
长治
临汾
最低气温
A、大同 B、太原 C、长治 D、临汾3. 21世纪以来,我国经济总量规模扩大了十倍,取得了举世瞩目的成就,2020年,我国国内生产总值达到101600亿元.数据101600用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 一个正方体的平面展开图如图所示,将它折成正方体后,与汉字“建”相对的面上的汉字是( ) A、文 B、明 C、霍 D、州6. 下图是由5个大小相同的正方体组成的立体图形,其俯视图是( )
A、文 B、明 C、霍 D、州6. 下图是由5个大小相同的正方体组成的立体图形,其俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、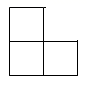 7. 如图, , C为的中点.点D在线段上,且 , 则的长度是( )
7. 如图, , C为的中点.点D在线段上,且 , 则的长度是( )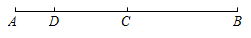 A、 B、 C、 D、8. 如图,已知∥ , , 平分 , 则的度数为( )
A、 B、 C、 D、8. 如图,已知∥ , , 平分 , 则的度数为( ) A、 B、 C、 D、9. 按如图所示的程序运算:当输入的数据为时,则输出的数据是( )
A、 B、 C、 D、9. 按如图所示的程序运算:当输入的数据为时,则输出的数据是( ) A、2 B、4 C、6 D、810. 如图,如果、 , 若 , 则的和是( )
A、2 B、4 C、6 D、810. 如图,如果、 , 若 , 则的和是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算:= .12. 若整式与是同类项,则的值是 .13. 如图,经过刨平的木板上的两个点,能弹出一条笔直的直线,并且只有一条,其中蕴含的数学道理是 .
 14. 某商品的售价为每件a元,为了参与市场竞争,商店按售价的九折再让利40元销售,此时该商品的售价为元.15. 如图是一组有规律的图案,它们是由边长相等的正三角形组合而成,第 个图案有 个三角形,第 个图案有 个三角形,第 个图案有 个三角形 按此规律摆下去,第 个图案有个三角形(用含 的代数式表示).
14. 某商品的售价为每件a元,为了参与市场竞争,商店按售价的九折再让利40元销售,此时该商品的售价为元.15. 如图是一组有规律的图案,它们是由边长相等的正三角形组合而成,第 个图案有 个三角形,第 个图案有 个三角形,第 个图案有 个三角形 按此规律摆下去,第 个图案有个三角形(用含 的代数式表示).
三、解答题
-
16. 计算(1)、(2)、17. 以下是马小虎同学化简代数式的过程.(1)、马小虎同学解答过程在第步开始出错,出错原因是 .(2)、请你帮助马小虎同学写出正确的解答过程.18. 在一张地图上有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚,但知道C在A地的北偏东方向,在B地南偏东方向.
 (1)、根据以上条件,在地图上画出C地的位置,并在图中标出相应的角度;(2)、直接写出的度数为 .19. 如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
(1)、根据以上条件,在地图上画出C地的位置,并在图中标出相应的角度;(2)、直接写出的度数为 .19. 如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y. (1)、用含有x、y的代数式表示图中“囧”的面积;(2)、当其中x=6、y=5时,求此时“囧”的面积.20. 补全下面的解题过程:
(1)、用含有x、y的代数式表示图中“囧”的面积;(2)、当其中x=6、y=5时,求此时“囧”的面积.20. 补全下面的解题过程:如图,∥ , , , .
 (1)、与的位置关系是 .(2)、对(1)中判断的与的位置关系加以证明.
(1)、与的位置关系是 .(2)、对(1)中判断的与的位置关系加以证明.证明:∵∥(已知),
∴= ▲ ( ),
∵(已知),
∴∠ ▲ (等量代换),
∵(已知),
∴∠ ▲
∵(已知),
∴ , ( )
∴∥( ).
21. 如图,已知直线和相交于点 , , 平分. (1)、写出与的大小关系: , 判断的依据是;(2)、若 , 求的度数.22. 数轴是非常重要的“数形结合”的工具之一,它揭示了数与点之间的内在联系,同时我们发现数轴上两点间的距离也与这两点所表示的数有关系.借助数轴完成下列任务:(1)、如图,A,B,C是数轴上依次排列的三个点,已知 , .
(1)、写出与的大小关系: , 判断的依据是;(2)、若 , 求的度数.22. 数轴是非常重要的“数形结合”的工具之一,它揭示了数与点之间的内在联系,同时我们发现数轴上两点间的距离也与这两点所表示的数有关系.借助数轴完成下列任务:(1)、如图,A,B,C是数轴上依次排列的三个点,已知 , .
①若点B表示的数为4,则在数轴上点A表示的数为 , 点C表示的数为 .
②若点B表示的数为-2,则在数轴上点A表示的数为 , 点C表示的数为 .
③若点B表示的数为m,则在数轴上点A表示的数为 , 点C表示的数为 .
(2)、从(1)的问题中发现:若点A、B在数轴上表示的数分别为a,b(且点A在点B的左侧)、那么= .(3)、在数轴上,若点E、F表示的数分别为、 , 那么= .(4)、若数轴上 , 点M表示的数是-2,求点N和线段的中点Р所表示的数分别是多少? 23. 问题情境
23. 问题情境在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
操作发现
 (1)、如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;(2)、如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;
(1)、如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;(2)、如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;结论应用
(3)、如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若 , 则∠CFG等于(用含的式子表示).