山西省晋城市阳城县2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-11-01 类型:期末考试
一、单选题
-
1. 多项式的项数及次数分别是( )A、3,2 B、3,3 C、2,3 D、3,42. 下列计算错误的是( )A、 B、 C、 D、3. 2020年,陕西省实现社会消费品零售总额9605.92亿元,将数字9605.92亿用科学记数法表示为( )A、 B、 C、 D、4. 若与可以合并成一项,则的值是( )A、2 B、8 C、16 D、325. 将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置,如果∠CDE=40°,那么∠BAF的大小为( )
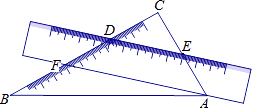 A、10° B、15° C、20° D、25°6. 根据流程图中的程序,当输入数值x为-2时,输出数值y为( )
A、10° B、15° C、20° D、25°6. 根据流程图中的程序,当输入数值x为-2时,输出数值y为( ) A、4 B、6 C、8 D、107. 骰子是一种特别的数字立方体(见下图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )
A、4 B、6 C、8 D、107. 骰子是一种特别的数字立方体(见下图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( ) A、
A、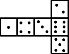 B、
B、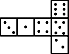 C、
C、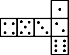 D、
D、 8. 观察如图所示的三种视图,与之对应的物体是( )
8. 观察如图所示的三种视图,与之对应的物体是( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 实数 , , 在数轴上的对应点的位置如图所示,则正确的结论是( )
9. 实数 , , 在数轴上的对应点的位置如图所示,则正确的结论是( )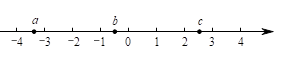 A、 B、 C、 D、10. 为了检验一条纸带的两条边线是否平行,小明沿折叠后,如图,测量得到:①;②;③;④ . 其中能够判定两条边线、互相平行的个数是( )
A、 B、 C、 D、10. 为了检验一条纸带的两条边线是否平行,小明沿折叠后,如图,测量得到:①;②;③;④ . 其中能够判定两条边线、互相平行的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 计算: .12. 计算的结果是 .13. 计算: .14. 已知线段 , 在线段上任取一点C,其中线段的中点为E、线段的中点为F.则线段的长度是 .15. 如图,如果小明在B,C之间经过D地,且C,D之间相距 , 则可以表示A,D之间的距离是 .
 16. 如图,四边形ABCD中,若去掉一个60°的角得到一个五边形,则∠1+∠2=
16. 如图,四边形ABCD中,若去掉一个60°的角得到一个五边形,则∠1+∠2=度.
 17. 如图,已知AB∥CD,CE平分∠ACD,交AB于点B,∠ABE=150°,则∠A为 .
17. 如图,已知AB∥CD,CE平分∠ACD,交AB于点B,∠ABE=150°,则∠A为 . 18. 学生在操场进行排队形,根据下图的排列方式(每个点代表一位学生),用字母表示第n个图形中学生的个数是 .
18. 学生在操场进行排队形,根据下图的排列方式(每个点代表一位学生),用字母表示第n个图形中学生的个数是 . 19. 如图,将长方形 沿 折叠,点C落在点Q处,点D落在AB边上的点E处.若 ,则 的等于 .
19. 如图,将长方形 沿 折叠,点C落在点Q处,点D落在AB边上的点E处.若 ,则 的等于 . 20. 润城枣糕是阳城的地方特产,小明妈妈做了m个枣糕售卖,有三个顾客先后来购买.第一位顾客买走了 , 小明妈妈又送给他一个;第二位顾客买走了剩下的 , 小明妈妈又送给她一个;第三位顾客再买走剩下的 , 小明妈妈又送给他一个,用代数式表示小明妈妈最后剩下的枣糕数是 .
20. 润城枣糕是阳城的地方特产,小明妈妈做了m个枣糕售卖,有三个顾客先后来购买.第一位顾客买走了 , 小明妈妈又送给他一个;第二位顾客买走了剩下的 , 小明妈妈又送给她一个;第三位顾客再买走剩下的 , 小明妈妈又送给他一个,用代数式表示小明妈妈最后剩下的枣糕数是 .
三、解答题
-
21.(1)、计算:;(2)、计算:;(3)、计算:;(4)、先化简,再求值: , 其中 .22. 如图,将长和宽分别是a、b的矩形纸片折成一个无盖的长方体纸盒,方案是在矩形纸片的四个角都剪去一个边长为x的正方形.
 (1)、用含a、b、x的代数式表示纸片剩余部分的面积;(2)、当 , 且剪去部分的正方形的边长为最小的正整数时,求无盖长方体纸盒的底面积;(3)、当 , 若x取整数,以x作为高,将纸片剩余部分折成无盖长方体,求长方体的体积最大值.23. 如图,直线 , 直角三角板的直角顶点A在直线上, , 线段与相交于点D,若 , 求的度数.抄写下面的解答过程,并填空(理由或数学式).
(1)、用含a、b、x的代数式表示纸片剩余部分的面积;(2)、当 , 且剪去部分的正方形的边长为最小的正整数时,求无盖长方体纸盒的底面积;(3)、当 , 若x取整数,以x作为高,将纸片剩余部分折成无盖长方体,求长方体的体积最大值.23. 如图,直线 , 直角三角板的直角顶点A在直线上, , 线段与相交于点D,若 , 求的度数.抄写下面的解答过程,并填空(理由或数学式).
解:过点B作 ,
∵( )
又∵( )
( )(等量代换)
又∵在中(已知)
∴( )
即( )(等式的性质)
∵ ,
∴
∴( )(两直线平行内错角相等)
24. 某家电集团公司研制生产的新家电,前期投资200万元,每生产一台这种新家电,后期还需投资0.3万元,已知每台新家电售价为0.5万元.设总投资为P万元,总利润为Q万元(总利润=总产值-总投资),新家电总产量为x台.(假设可按售价全部卖出)(1)、试用x的代数式表示P和Q;(2)、当总产量达到900台时,该公司能否盈利?(3)、当总产量达到多少台时,该公司开始盈利?

