浙江省温州市2022-2023学年九年级上学期第一次月考数学试题

试卷更新日期：2022-11-01 类型：月考试卷

进入出卷网下载

一、单选题

1. 有10张背面完全相同的卡片，正面分别写有数字：1至10，把这些卡片背面朝上洗匀后，从中随机抽取三张卡片a，b，c，则这三张卡片a，b，c的数字正好是直角三角形的三边长的概率是（）

A、 $\frac{1}{120}$ B、 $\frac{1}{60}$ C、 $\frac{1}{45}$ D、 $\frac{1}{72}$

查看试题解析
2. 已知⊙O的半径为13，弦AB∥CD，AB=24，CD=10，则四边形ACDB的面积是（）

A、119 B、289 C、77或119 D、119或289

查看试题解析
3. 如图， $△ A D C$ 是由等腰直角 $△ E O G$ 经过位似变换得到的，位似中心在 $x$ 轴的正半轴，已知 $E O = 1$ ， $D$ 点坐标为 $D (2 ， 0)$ ，位似比为 $1 ： 2$ ，则两个三角形的位似中心 $P$ 点的坐标是（）

A、 $(\frac{2}{3} ， 0)$ B、 $(1 ， 0)$ C、 $(0 ， 0)$ D、 $(\frac{1}{3} ， 0)$

查看试题解析
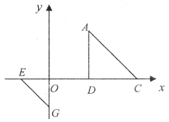4. 定义：我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图，在正方形 $O A B C$ 中，点 $A (0 ， 2)$ ，点 $C (2 ， 0)$ ，则互异二次函数 $y = {(x - m)}^{2} - m$ 与正方形 $O A B C$ 有交点时 $m$ 的最大值和最小值分别是（）

A、4，-1 B、 $\frac{5 - \sqrt{17}}{2}$ ，-1 C、4，0 D、 $\frac{5 + \sqrt{17}}{2}$ ，-1

查看试题解析
5. 如图，在△ABC中， $∠ C = 90 °$ ， $A C = B C = 6$ ，点D，E分别在AC和BC上， $C D = 2$ ，若以DE为直径的⊙O交AB的中点F，则⊙O的直径是（）

A、 $2 \sqrt{3}$ B、2 C、 $2 \sqrt{5}$ D、5

查看试题解析
6. 如图，△ABC为等腰直角三角形，∠BAC＝90°，AB＝AC＝2，点D为△ABC所在平面内一点，∠BDC＝90°，以AC、CD为边作平行四边形ACDE，则CE的最小值为（）

A、 $\sqrt{10} - \sqrt{2}$ B、 $3 - \sqrt{2}$ C、 $\frac{7}{5}$ D、 $2 \sqrt{3} - \sqrt{2}$

查看试题解析
7. 如图1，是清代数学家李之铉在他的著作《几何易简集》中研究过的一个图形，小圆同学在研究该图形后设计了图2，延长正方形 $A B C D$ 的边 $B C$ 至点 $M$ ，作矩形 $A B M N$ ，以 $B M$ 为直径作半圆 $O$ 交 $C D$ 于点 $E$ ，以 $C E$ 为边做正方形 $C E F G$ ， $G$ 在 $B C$ 上，记正方形 $A B C D$ ，正方形 $C E F G$ ，矩形 $C M N D$ 的面积分别为 $S_{1}$ ， $S_{2}$ ， $S_{3}$ ，则 $\frac{S_{1}}{S_{2} + S_{3}} =$ （）

A、 $\frac{3 + \sqrt{5}}{4}$ B、 $\frac{1 + \sqrt{5}}{2}$ C、 $\frac{3 + \sqrt{2}}{4}$ D、 $\frac{1 + \sqrt{2}}{2}$

查看试题解析
8. 如图，矩形 $A B C D$ 中， $E$ 是 $B C$ 上一点，连接 $A E$ ，将矩形沿 $A E$ 翻折，使点 $B$ 落在 $C D$ 边 $F$ 处，连接 $A F$ ，在 $A F$ 上取点 $O$ ，以 $O$ 为圆心， $O F$ 长为半径作⊙O与 $A D$ 相切于点 $P$ .若 $A B = 6$ ， $B C = 3 \sqrt{3}$ ，则下列结论：① $F$ 是 $C D$ 的中点；②⊙O的半径是2；③ $A E = 3 C E$ ；④S_阴影 $= \frac{\sqrt{3}}{2}$ .其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图，抛物线 $y = - x^{2} + 2 x + 1$ 交x轴于A，B两点，交y轴于点C，点D为抛物线的顶点，点C关于抛物线的对称轴的对称点为点E，点G，F分别在x轴和y轴上，则四边形EDFG周长的最小值为（）

A、6 B、 $4 \sqrt{2}$ C、 $\sqrt{30}$ D、 $2 \sqrt{7}$

查看试题解析
10. 如图，边长为6的正方形ABCD中，E、F是对角线AC的三等分点，连接BE并延长交AD于点G，连接GF并延长交BC于点H，记△GEF的面积为m，△CHF的面积为n，则m+n的值为（）

A、 $\frac{9}{2}$ B、6 C、 $\frac{15}{2}$ D、7

查看试题解析

二、填空题

11. 若实数a是一元二次方程x²-3x+1=0的一个根，则a³+ $\frac{24}{a^{2} + 1}$ 的值为.

查看试题解析
12. 温故知新：若满足不等式 $\frac{8}{15} < \frac{n}{n + k} < \frac{7}{13}$ 的整数k只有一个，则正整数n的最大值．
阅读理解：任意正整数 $a$ ， $b$ ， ∵ ${(\sqrt{a} - \sqrt{b})}^{2} \geq 0$ ， ∴ $a - 2 \sqrt{a b} + b \geq 0$ ， ∴ $a + b ≥ 2 \sqrt{a b}$ ，只有当 $a = b$ 时，等号成立；结论：在 $a + b ≥ 2 \sqrt{a b}$ （ $a$ 、 $b$ 均为正实数）中，只有当 $a = b$ 时， $a + b$ 有最小值 $2 \sqrt{a b}$ ．若 $m > 1$ ， $\sqrt{m} + \frac{1}{\sqrt{m} - 1}$ 有最小值为．

查看试题解析
13. 如图是一个小圆同学设计的一个鱼缸截面图，弓形 $A C B$ 是由优弧 $A B$ 与弦 $A B$ 组成， $A C$ 是鱼缸的玻璃隔断，弓形 $A C$ 部分不注水，已知 $C D ⊥ A B$ ，且圆心 $O$ 在 $C D$ 上， $A B = C D = 80 c m$ ．注水时，当水面恰好经过圆心时，则水面宽 $E F$ 为 $c m$ ；注水过程中，求水面宽度 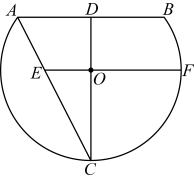$E F$ 的最大值为 $c m$ ．

查看试题解析
14. 已知抛物线y₁：y＝2（x﹣3）²+1和抛物线y₂：y＝﹣2x²﹣8x﹣3，若无论k取何值，直线y＝kx+km+n被两条抛物线所截的两条线段都保持相等，则m＝， n＝．

查看试题解析
15. 工人师傅在修茸一人字架屋顶BAC时需要加固，计划焊接三根钢条AD，DE，FG．在如图所示的△ABC中，AB=AC=10，BC=12，AD⊥BC于点D，点E，F，G分别是AB，BD，AC上的点，连接DE，GF，交于点H，GF与AD交于点M，当H为FM的中点，BF∶CF=1∶5，AG：AE=5：7时，△AGM的面积为．

查看试题解析
16. 图甲是一款设计师工作台灯，它的主要构件是上下两条旋转臂和一盏条形灯.设计师工作时，常常通过转动旋转臂和灯来调节光源的位置，获得需要的光照效果图乙表示了设计师两次调节过程，他先转动下旋转臂 $B C$ ，使点 $C$ 到桌面的距高 $C P = 20 c m$ ，然后转动上旋转臂 $C D$ 和灯 $D E$ ，使 $D E$ 与桌面 $B G$ 平行，且 $∠ E D C = ∠ G B C$ .调好后他感觉光照效果不佳，于是再转动上旋转臂和灯，使得上旋转臂 $D^{'} C ⊥ B C$ ，同时灯 $D^{'} E^{'} / / B G$ .若已知上旋转臂 $C D = 60 c m$ ，第二次调整后灯向右移动的水平距离 $Q E^{'} = 10 c m$ ，则第二次调整结束后灯距高桌面的高度 $Q R =$ $c m$ .

查看试题解析

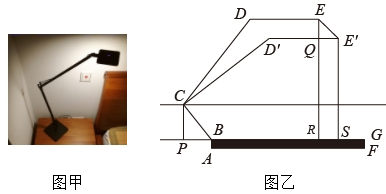
三、解答题

17. 如图，已知二次函数G₁：y＝ax²+bx+c（a≠0）的图象过点（﹣1，0）和（0，3），对称轴为直线x＝1．

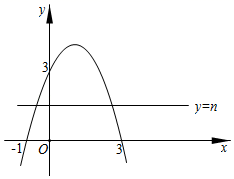(1)、求二次函数G₁的解析式；

(2)、当﹣1＜x＜2时，求函数G₁中y的取值范围；

(3)、将G₁先向右平移3个单位，再向下平移2个单位，得到新二次函数G₂ ，则函数G₂的解析式是．

(4)、当直线y＝n与G₁、G₂的图象共有4个公共点时，直接写出n的取值范围．

查看试题解析
18. 已知圆O的半径长为2，点A、B、C为圆O上三点，弦 $B C = A O$ ，点D为BC的中点，

(1)、如图，连接AC、OD，设 $∠ O A C = α$ ，请用α表示 $∠ A O D$ ；

(2)、如图，当点B为 $\overset{⌢}{A C}$ 的中点时，求点A、D之间的距离．

(3)、如果AD的延长线与圆O交于点E，以O为圆心，AD为半径的圆与以BC为直径的圆有且只有一个交点，求弦AE的长．

查看试题解析
19. 已知如图，E、F分别在四边形ABCD边AB、BC上，在CD上求作一点P，使 $∠ E P F = ∠ B E F$ ．（不写作法，保留作图痕迹）

查看试题解析
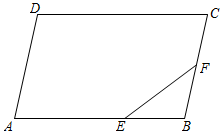20. 阅读材料：各类方程的解法：求解一元一次方程，根据等式的基本性质，把方程转化为 $x = a$ 的形式，求解二元一次方程组，把它转化为一元一次方程来解；类似的，三元一次方程组，把它转化为解二元一次方程组．求解一元二次方程，把它转化为两个一元一次方程来解．求解分式方程，把它转化为整式方程来解，由于“去分母”可能产生增根，所以解分式方程必须检验．各类方程的解法不尽相同，但是它们有一个共同的基本数学思想——转化，把未知转化为已知．

(1)、问题：方程 $6 x^{3} + 14 x^{2} - 12 x = 0$ 的解是： $x_{1} = 0$ ， $x_{2} =$ ， $x_{3} =$ ；

(2)、拓展：用“转化”思想求方程 $\sqrt{2 x + 3} = x$ 的解；

(3)、应用：如图，矩形草坪 $A B C D$ 的长 $A D = 21 m$ ，宽 $A B = 8 m$ ，点 $P$ 在 $A D$ 上（ $A P ＞ P D$ ），小华把一根长为27m的绳子一段固定在点 $B$ ，把长绳 $P B$ 段拉直并固定在点 $P$ ，再拉直，长绳的另一端恰好落在点 $C$ ，求 $A P$ 的长．

查看试题解析
21.

(1)、把长为 $a$ 的线段任意分成3条线段，求这3条线段能够构成一个三角形的3条边的概率．

(2)、据统计，2008年底该市汽车拥有量为75万辆，而截止到2010年底，该市的汽车拥有量已达108万辆．为了保护环境，缓解汽车拥堵，该市拟控制汽车总量，要求到2012年底全市汽车拥有量不超过125.48万辆；且从2011年初起，该市此后每年报废的汽车数量是上年底汽车拥有量的 $10 %$ ．假设每年新增汽车数量相同，请估算出该市从2011年初起每年新增汽车数量最多不超过多少万辆，并求出求2008年底至2010年底该市汽车拥有量的年平均增长率．

查看试题解析
22. 在平面直角坐标系中，二次函数 $y = x^{2} - 2 m x + 6 m$ （ $x \leq 2 m$ ， m为常数）的图象记作G，图象G上点A的横坐标为2m．

(1)、当 $m = 1$ ，求图象G的最低点坐标；

(2)、平面内有点 $C (- 2 ， 2)$ ．当AC不与坐标轴平行时，以AC为对角线构造矩形ABCD，AB与x轴平行，BC与y轴平行．
①若矩形ABCD为正方形时，求点A坐标；
②图象G与矩形ABCD的边有两个公共点时，求m的取值范围．

查看试题解析

23. 某工厂每月生产800件产品，每件产品成本100元，分配给线下直营店和线上旗舰店两个渠道销售．线下直营店的产品按照定价190元出售，并进行促销活动：月销量不超过400件的部分，每件产品赠送成本为60元的礼品，可全部售完；超过400 件的部分，因礼品已送完，则需要再一次性投入成本为5000元的广告进行宣传，也可全部售完．线上旗舰店的产品售价

y

（元）与月销量

x

（件）满足关系：

y = - \frac{1}{8} x + 230

．（销售利润

=

销售收入-成本）

(1)、分别用含

a ， b

的代数式表示：

①线下直营店的月销量为 $a$ 件．若 $0 ⩽ a ⩽ 400 ，$ 这 $a$ 件产品的销售利润为元；若 $400 < a ⩽ 800 ，$ 这 $a$ 件产品的销售利润为元．

②线上旗舰店的月销量为 $b$ 件，这 $b$ 件产品的销售利润为元．

(2)、假设800件产品每月都能售出．

①若平均分配给两个渠道进行销售，求这800件产品的销售总利润．

②请设计一种与①不同的分配方案，根据方案评价表，确定方案类型并填表．（不同方案得分不同，具体见表）

线下直营店分配数量		线上旗舰店分配数量	你的方案类型（填优秀、良好或合格）
件		件
方案评价表（利润单位：元）
优秀方案	月总利润 $> 46190$	4 分
良好方案	$44000 <$ 月总利润 $⩽ 46190$	2 分
合格方案	$40000 <$ 月总利润 $⩽ 44000$	1 分

查看试题解析

24. 四边形的一条对角线将这个四边形分成两个三角形，如果这两个三角形相似（不全等），那么我们将这条对角线叫做这个四边形的相似对角线．

(1)、如图1，四边形ABCD中，∠DAB＝100°，∠DCB＝130°，对角线AC平分∠DAB，求证：AC是四边形ABCD的相似对角线；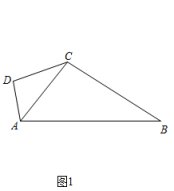

(2)、如图2，直线 $y = - \frac{\sqrt{3}}{3} x + \frac{4 \sqrt{3}}{3}$ 分别与x，y轴相交于A，B两点，P为反比例函数y＝ $\frac{k}{x}$ （k＜0）上的点，若AO是四边形ABOP的相似对角线，求反比例函数的解析式；

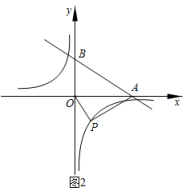(3)、如图3，AC是四边形ABCD的相似对角线，点C的坐标为（3，1），AC∥x轴，∠BCA＝∠DCA＝30°，连接BD，△BCD的面积为 $\sqrt{3}$ ．过A，C两点的抛物线y＝ax²+bx+c（a＜0）与x轴交于E，F两点，记|m|＝AC+1，若直线y＝mx与抛物线恰好有3个交点，求实数a的值．

查看试题解析