浙江省衢州市2022-2023学年九年级上学期第一次调研检测数学模拟试题

试卷更新日期：2022-11-01 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、等边三角形； B、等腰梯形； C、平行四边形； D、正十边形

查看试题解析
2. 若 $⊙ A$ 的半径为5，圆心 $A$ 的坐标为 $(3 ， 4)$ ，点 $P$ 的坐标是 $(3 ， - 1)$ ，则点 $P$ 与 $⊙ A$ 的位置关系是（）．

A、 $P$ 在 $⊙ A$ 上 B、 $P$ 在 $⊙ A$ 外 C、 $P$ 在 $⊙ A$ 内 D、以上答案都不对

查看试题解析
3.
为吸引顾客，石景山万达广场某餐饮店推出转盘抽奖打折活动，如图是可以自由转动的转盘，转盘被分成若干个扇形，转动转盘，转盘停止后，指针所指区域内的奖项可作为打折等级（若指针指向两个扇形的交线时，重新转动转盘），其中一等奖打九折，二等奖打九五折，三等奖赠送小礼品．小明和同学周六去就餐，他们转动一次转盘能够得到九折优惠的概率是

A、 $\frac{1}{3}$ B、 $\frac{2}{7}$ C、 $\frac{3}{16}$ D、 $\frac{1}{8}$

查看试题解析
4. 已知三个数1，2，4，若添一个数使得四个数成比例，这个数可以是（）

A、8 B、 $- 8$ C、3 D、 $- 3$

查看试题解析
5. 已知 $\frac{x}{y} ＝ \frac{3}{2}$ ，那么下列等式中，不一定正确的是（）

A、 $x + y = 5$ B、 $2 x = 3 y$ C、 $\frac{x + y}{y} ＝ \frac{5}{2}$ D、 $\frac{x}{x + y} ＝ \frac{3}{5}$

查看试题解析
6. 如图，点 $D$ 、 $E$ 分别是 $△ A B C$ 边 $B A$ 、 $B C$ 的中点， $△ A B C$ 的面积等于 $8$ ，则 $△ B D E$ 的面积为（）

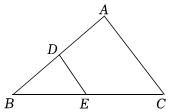A、2 B、3 C、4 D、5

查看试题解析
7. 如果将抛物线向右平移2个单位后得到 $y = x^{2}$ ，那么原抛物线的表达式是（）

A、 $y = x^{2} + 2$ B、 $y = x^{2} - 2$ C、 $y = (x + 2)^{2}$ D、 $y = (x - 2)^{2}$

查看试题解析
8. 下列各函数中，y随x增大而增大的是（）

A、y=-x+1 B、 $y = - \frac{3}{x}$ C、 $y = x^{2} + 1$ D、y=2x-3

查看试题解析
9. 等腰三角形的顶角为120°，腰长为6，则它底边上的高等于（）

A、3 B、8 C、9 D、7

查看试题解析
10. 农夫将苹果树种在正方形的果园内，为了保护苹果树不受风吹，他在苹果树的周围种上针叶树．在下图里，你可以看到农夫所种植苹果树的列数（n）和苹果树数量及针叶树数量的规律：当n为某一个数值时，苹果树数量会等于针叶树数量，则n为（）

A、6 B、8 C、12 D、16

查看试题解析

二、填空题

11. 抛物线 $y = - \frac{1}{2} x^{2} + 3 x$ 的开口方向是．（选填“向上”或“向下”）

查看试题解析
12. 在比例尺是1：15000000的地图上，测得甲乙两地的距离是2厘米，那么甲乙两地的实际距离是千米．

查看试题解析
13. 一个布袋中装有只有颜色不同的a（ $a > 12$ ）个小球，分别是2个白球、4个黑球，6个红球和b个黄球，从中任意摸出一个球，记下颜色后放回，经过多次重复实验，把摸出白球，黑球，红球的概率绘制成统计图（未绘制完整）．根据题中给出的信息，布袋中黄球的个数为．

查看试题解析
14. 在平面直角坐标系xOy中，有一个边长为2个单位长度的等边△ABC，满足AC∥y轴．平移△ABC得到△A′B′C′，使点A′、B′分别在x轴、y轴上（不包括原点），则此时点C′的坐标是．.

查看试题解析
15. 已知等腰直角三角形ABC的BC边上的高为3，则△ABC的面积为.

查看试题解析
16. 如图，四边形ABCD中，∠ADC＝90°，AC⊥BC，∠ABC＝45°，AC与BD交于点E，若AB＝ $2 \sqrt{10}$ ， CD＝2，则△ABE的面积为．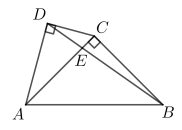

查看试题解析

三、解答题

17. 在A市建设规划图上，城区南北长为240cm，A市城区南北的实际长为18km，试写出该规划图的比例尺.

查看试题解析
18. 小丹有3张扑克牌，小林有2张扑克牌，扑克牌上的数字如图所示．两人用这些扑克牌做游戏，他们分别从自己的扑克牌中随机抽取一张，比较这两张扑克牌上的数字大小，数字大的一方获胜．请用画树状图（或列表）的方法，求小丹获胜的概率．

查看试题解析
19.
以图中的格点为顶点，画一个与已知△ABC相似的三角形（相似比不为1）．

查看试题解析
20. 如图，在每个小正方形的边长均为1的方格纸中有线段AB和CD，点A、B、C、D均在小正方形的顶点上．

（ 1 ）画出一个以AB为一直角边的Rt△ABE，点E在小正方形的顶点上，且∠BAE＝45°；
（ 2 ）画出一个以CD为一边的菱形CDMN，点M、N均在小正方形的顶点上，且菱形CDMN的面积是△ABE面积的4倍，连接EN，请直接写出线段EN的长．

查看试题解析
21. 已知抛物线y＝x²+bx+c经过A（1，0），B（0，2）两点，顶点为D.

(1)、求抛物线的解析式；

(2)、将△OAB绕点A顺时针旋转90°后，点B落到点C的位置，将抛物线沿y轴平移后经过点C，求平移后所得图象的函数关系式.

查看试题解析
22. 如图，在 $Δ A B C$ 中， $∠ B A C = 90 °$ ， $A D$ 是 $B C$ 边上的高， $E$ 是 $B C$ 边上的一个动点（不与 $B$ ， $C$ 重合）， $E F ⊥ A B$ ， $E G ⊥ A C$ ，垂足分别为 $F$ ， $G$ .

(1)、求证： $\frac{E G}{A D} = \frac{C G}{C D}$ ；

(2)、 $F D$ 与 $D G$ 是否垂直？若垂直，请给出证明，若不垂直，请说明理由.

查看试题解析
23. 如图，在正方形ABCD中，点M是边BC上的一点（不与B、C重合），点N在CD边的延长线上，且满足∠MAN＝90°，联结MN、AC，MN与边AD交于点E.

(1)、求证：AM＝AN；

(2)、如果∠CAD＝2∠NAD，求证：AM²＝AC•AE；

(3)、MN和AC相交于O点，若BM＝1，AB＝3，试猜想线段OM，ON的数量关系并证明.

查看试题解析
24. 直线 $A B // C D$ ， $E$ 是 $A B$ 上一定点， $P$ 是直线 $C D$ 上一动点，点 $Q$ 在直线 $A B$ ， $C D$ 之间，且 $∠ Q P D = 70 °$ ， $∠ Q E B = α$ ， $∠ C P Q$ 的平分线交直线 $A B$ 于点 $M$ ．

(1)、如图1，若 $α = 65 °$ ，则 $∠ E Q P$ 的度数是°．

(2)、如图2，若 $P M // E Q$ ，求 $∠ Q E B$ 的度数；

(3)、若 $∠ M E Q$ 的角平分线交 $P M$ 于点 $N$ ，求 $∠ E N P$ 的度数（用含 $α$ 的式子表示）．

查看试题解析