浙江省杭州市萧山区六校2022-2023学年九年级上学期10月月考数学试题
试卷更新日期:2022-11-01 类型:月考试卷
一、单选题
-
1. 下列y和x之间的函数表达式中,属于二次函数的是( )A、 B、 C、 D、2. 下列判断正确的是( )A、天气预报说“明天的降水概率为60%”,则表示明天有60%的时间都在降雨 B、掷一枚硬币正面朝上的概率为 , 则表明掷硬币8次,一定有4次正面朝上 C、“篮球队员在罚球线上投篮一次,投中”为必然事件 D、若a是实数,则3. 抛物线y=2x2﹣4x﹣3的顶点坐标为( )A、(1,5) B、(1,﹣5) C、(﹣1,5) D、(﹣1,﹣5)4. 关于二次函数的最值,下列说法正确的是( )A、有最大值2 B、有最小值2 C、有最大值3 D、有最小值35. 将五张分别画有线段、等边三角形、平行四边形、矩形、正六边形的卡片任意摆放,将有图形的一面朝下,从中任意翻开一张卡片,图形既是轴对称图形又是中心对称图形的概率为( )A、 B、 C、 D、6. 将抛物线向左平移2个单位,再向上平移4个单位,所得抛物线的解析式是( )A、 B、 C、 D、7. 已知 , , 是上的点,则对 , 和的大小关系判断正确的是( )A、 B、 C、 D、8. 已知抛物线的对称轴为直线 , 则关于x的不等式的取值范围是( )A、 B、 C、 D、9. 已知非负数 , 满足且 , 设的最大值为 , 最小值为 , 则的值是( )A、1 B、2 C、3 D、410. 如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1 , 将C1向右平移得C2 , C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
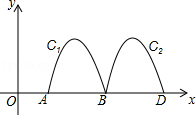 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 一个质地均匀的骰子,其六面上分别标有数字1,2,3,4,5,6,投掷一次,朝上一面的数字小于4的概率为.12. 已知函数 , 当x时,y随x的增大而增大.13. 抛物线关于y轴对称的抛物线解析式为 .14. 已知抛物线与x轴交点的横坐标为 , 则 .15. 已知关于x的方程 的两个根分别是 , , 若点P是二次函数 的图象与y轴的交点,过P作轴交抛物线于另一交点Q,则PQ的长为 .16. 已知函数(b,c为常数)的图像经过点 , .(1)、当时,y的最大值为.(2)、当时,若y的最大值与最小值之和为-1,则m的值为.
三、解答题
-
17. 有一盒子中装有6个乒乓球,除颜色外形状和大小完全一样,其中3个黑色乒乓球,2个白色乒乓球,1个红色乒乓球.王海同学从盒子中任意摸出一乒乓球.(1)、你认为王海同学摸出的球,最有可能是颜色;(2)、王海和陈星同学一起做游戏,王海或陈星从上述盒子中任意摸一球,如果摸到黑球,王海获胜,否则陈星获胜.请问这个游戏对双方公平吗?为什么?18. 如图,已知直线l: 经过A(2,0)和B(0,2)两点,它与抛物线在第一象限内相交于点P,且的面积为1.
 (1)、求点P的坐标.(2)、求a的值,并写出抛物线的解析式.19. 已知二次函数:(1)、若二次函数图象与x轴有交点,求m的取值范围.(2)、当二次函数的图象经过点时,确定m的值,并求出此二次函数与坐标轴的交点坐标.20. 如图,在平面直角坐标系中,二次函数的图象顶点是A,与x轴交于B,C两点,与y轴交于点D.其中点B的坐标是 .
(1)、求点P的坐标.(2)、求a的值,并写出抛物线的解析式.19. 已知二次函数:(1)、若二次函数图象与x轴有交点,求m的取值范围.(2)、当二次函数的图象经过点时,确定m的值,并求出此二次函数与坐标轴的交点坐标.20. 如图,在平面直角坐标系中,二次函数的图象顶点是A,与x轴交于B,C两点,与y轴交于点D.其中点B的坐标是 . (1)、求A,C两点的坐标,并根据图象直接写出当时x的取值范围.(2)、平移该二次函数的图象,使点D恰好落在点A的位置上,求平移后图象所对应的二次函数的表达式.21. 杭州亚运会已进入倒计时,垃圾分类被上级部门视为其中一项重要工作,因此环保部门计划再订制一些宣传海报,要求海报版面不小于 平方米,当宣传海报的版面为 平方米时,价格为元/平方米.为了支持此项工作,广告公司给予以下优惠:宣传海报版面每增加平方米,每平方米的价格减少元,但不能低于元/平方米.假设宣传海报的版面增加平方米后,总费用为元.(1)、求关于的函数表达式(需列式化简);(2)、订制宣传海报的版面为多少平方米时总费用最高?最高费用为多少元?
(1)、求A,C两点的坐标,并根据图象直接写出当时x的取值范围.(2)、平移该二次函数的图象,使点D恰好落在点A的位置上,求平移后图象所对应的二次函数的表达式.21. 杭州亚运会已进入倒计时,垃圾分类被上级部门视为其中一项重要工作,因此环保部门计划再订制一些宣传海报,要求海报版面不小于 平方米,当宣传海报的版面为 平方米时,价格为元/平方米.为了支持此项工作,广告公司给予以下优惠:宣传海报版面每增加平方米,每平方米的价格减少元,但不能低于元/平方米.假设宣传海报的版面增加平方米后,总费用为元.(1)、求关于的函数表达式(需列式化简);(2)、订制宣传海报的版面为多少平方米时总费用最高?最高费用为多少元?