2022-2023浙教版数学七年级上册6.2线段、射线、直线 课后测验
试卷更新日期:2022-10-31 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,这一实际问题应用的数学知识是( )A、两点确定一条直线 B、两点之间直线最短 C、两点之间线段最短 D、直线有两个端点2. 植树时,只要确定两棵树的位置,就能确定同一行树所在的直线,理由是( )A、两点确定一条直线 B、两点间距离的定义 C、两点之间,线段最短 D、因为省力3. 如图,点 为线段 上一点,则图中线段的条数为( )
 A、1条 B、2条 C、3条 D、4条4. 下列说法正确的是( )A、直线 B、射线 C、直线 与直线 是同一条直线 D、射线 与射线 是同一条射线5. 下列说法正确的是( )A、一点确定一条直线 B、射线比直线短 C、两点之间,线段最短 D、若AB=BC,则B为AC的中点6. 下列各图形中,有交点的是 ( )A、
A、1条 B、2条 C、3条 D、4条4. 下列说法正确的是( )A、直线 B、射线 C、直线 与直线 是同一条直线 D、射线 与射线 是同一条射线5. 下列说法正确的是( )A、一点确定一条直线 B、射线比直线短 C、两点之间,线段最短 D、若AB=BC,则B为AC的中点6. 下列各图形中,有交点的是 ( )A、 B、
B、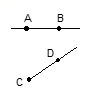 C、
C、 D、
D、 7. 如图,已知三点A,B,C画直线AB,画射线AC,连接BC,按照上述语句画图正确的是( )A、
7. 如图,已知三点A,B,C画直线AB,画射线AC,连接BC,按照上述语句画图正确的是( )A、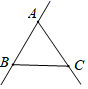 B、
B、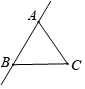 C、
C、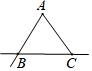 D、
D、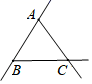 8. 如图,点 、 、 在同一条直线上,则下列说法正确的是( )
8. 如图,点 、 、 在同一条直线上,则下列说法正确的是( )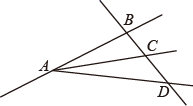 A、射线 和射线 是同一条射线 B、直线 和直线 是同一条直线 C、图中只有 条线段 D、图中有 条直线9. 在下列生活、生产现象中,不可以用基本事实“两点确定一条直线”来解释的有( )
A、射线 和射线 是同一条射线 B、直线 和直线 是同一条直线 C、图中只有 条线段 D、图中有 条直线9. 在下列生活、生产现象中,不可以用基本事实“两点确定一条直线”来解释的有( )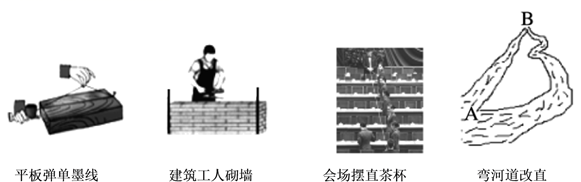 A、1个 B、2个 C、3个 D、4个10. 如果线段AB=3cm,BC=1cm,那么A、C两点的距离d的长度为( )A、4cm B、2cm C、4cm或2cm D、小于或等于4cm,且大于或等于2cm
A、1个 B、2个 C、3个 D、4个10. 如果线段AB=3cm,BC=1cm,那么A、C两点的距离d的长度为( )A、4cm B、2cm C、4cm或2cm D、小于或等于4cm,且大于或等于2cm二、作图题(共2题,共18分)
-
11. 如图,已知 , , , 四个点,按要求画出图形.
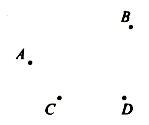 (1)、①画直线 , 相交于点 ;
(1)、①画直线 , 相交于点 ;②画射线 :
③连接 ;
(2)、图中共有条线段.12. 如图 按下列语句画图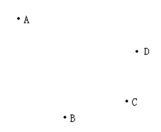
( 1 )连接BC.
( 2 )画直线AB、CD相交于E.
( 3 )作射线AD.
( 4 )连接AC、BD,相交于点O.
三、解答题(共3题,共32分)
-
13. 如图所示,线段AB上的点数与线段的总数有如下关系:如果线段AB上有3个点时,线段总数共有3条,如果AB上有4个点时,线段总数共有6条,如果线段AB上有5个点时,线段总数共有10条,….
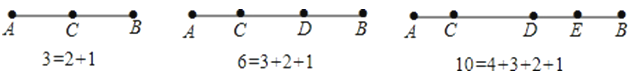
(1)当线段AB上有6个点时,线段总数共有多少条?
(2)当线段AB上有n个点时,线段总数共有多少条?(用含n的式子表示)
(3)当n=100时,线段总数共有多少条?
14. 如图 (1)、【观察思考】如图线段AB上有两个点C、D,分别以点A、B、C、D为端点的线段共有条(2)、【模型构建】若线段上有m个点(包括端点),则该线段上共有条线段(3)、【拓展应用】若有8位同学参加班级的演讲比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),请你应用上述模型构建,求一共要进行多少场比赛?15. 数形结合思想是通过数和形之间的对应关系和相互转化来解决问题的数学思想方法.我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事休.”(1)、(问题背景)往返于甲、乙两地的客车,中途停靠2个车站(来回票价一样),可以从任意站点头票出发且任意两站间的票价都不同,共有种不同的票价,需准备种车票.
(1)、【观察思考】如图线段AB上有两个点C、D,分别以点A、B、C、D为端点的线段共有条(2)、【模型构建】若线段上有m个点(包括端点),则该线段上共有条线段(3)、【拓展应用】若有8位同学参加班级的演讲比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),请你应用上述模型构建,求一共要进行多少场比赛?15. 数形结合思想是通过数和形之间的对应关系和相互转化来解决问题的数学思想方法.我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事休.”(1)、(问题背景)往返于甲、乙两地的客车,中途停靠2个车站(来回票价一样),可以从任意站点头票出发且任意两站间的票价都不同,共有种不同的票价,需准备种车票.
聪明的小周是这样思考这个问题的,她用 , , , , 4个点表示车站,每两站之间的票价用相应两点间的线段表示,共连出多少条线段,就有多少种不同的票价.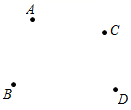 (2)、(迁移应用) , , , , , 六支足球队进行单循环比赛,当比赛到某一天时,统计出 , , , , 五支队已经分别比赛了 , , , , 场球,则还没有与 队比赛的球队是队.(3)、(拓展创新)某摄制组从 市到 市有一天的路程,计划上午比下午多走100千米到 市吃午饭,但由于堵车,中午才赶到一个小镇,只行驶了上午原计划的三分之一,过了小镇,汽车行驶了400千米,傍晚才停下来休息,司机说,再走从 市到这里的路程的二分之一就到达目的地了,求 , 两市相距多少千米?
(2)、(迁移应用) , , , , , 六支足球队进行单循环比赛,当比赛到某一天时,统计出 , , , , 五支队已经分别比赛了 , , , , 场球,则还没有与 队比赛的球队是队.(3)、(拓展创新)某摄制组从 市到 市有一天的路程,计划上午比下午多走100千米到 市吃午饭,但由于堵车,中午才赶到一个小镇,只行驶了上午原计划的三分之一,过了小镇,汽车行驶了400千米,傍晚才停下来休息,司机说,再走从 市到这里的路程的二分之一就到达目的地了,求 , 两市相距多少千米?四、填空题(每空2分,共20分)
-
16. 王小毛同学做教室卫生时,发现座位很不整齐,他思考了一下,将第一座和最后一座固定之后,沿着第一座最后一座这条线就把座位摆整齐了!他利用了数学原理: .
 17. 要把一根木条固定在墙上,至少要钉2个钉子,这是因为 .
17. 要把一根木条固定在墙上,至少要钉2个钉子,这是因为 .