2022年苏科版初中数学七年级上册 6.5 垂直 同步练习
试卷更新日期:2022-10-30 类型:同步测试
一、夯实基础
-
1. 下列图形中线段PQ的长度表示点P到直线a的距离的是( )A、
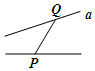 B、
B、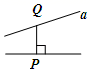 C、
C、 D、
D、 2. 点P是直线外一点,为直线上三点, , 则点P到直线的距离是( )A、2cm B、小于2cm C、不大于2cm D、4cm3. 下列说法错误的是( )A、平面内过一点有且只有一条直线与已知直线平行 B、平面内过一点有且只有一条直线与已知直线垂直 C、两点之间的所有连线中,线段最短 D、对顶角相等4. 如图所示, ,垂足分别为A、D,已知 ,则点A到线段 的距离是( )
2. 点P是直线外一点,为直线上三点, , 则点P到直线的距离是( )A、2cm B、小于2cm C、不大于2cm D、4cm3. 下列说法错误的是( )A、平面内过一点有且只有一条直线与已知直线平行 B、平面内过一点有且只有一条直线与已知直线垂直 C、两点之间的所有连线中,线段最短 D、对顶角相等4. 如图所示, ,垂足分别为A、D,已知 ,则点A到线段 的距离是( ) A、10 B、8 C、6 D、4.85. 如图,已知点A是射线BE上一点,过A作AC⊥BF,垂足为C,CD⊥BE,垂足为D.给出下列结论:①∠1是∠ACD的余角;②图中互余的角共有3对;③∠1的补角只有∠DCF;④与∠ADC互补的角共有3个.其中正确结论有( )
A、10 B、8 C、6 D、4.85. 如图,已知点A是射线BE上一点,过A作AC⊥BF,垂足为C,CD⊥BE,垂足为D.给出下列结论:①∠1是∠ACD的余角;②图中互余的角共有3对;③∠1的补角只有∠DCF;④与∠ADC互补的角共有3个.其中正确结论有( )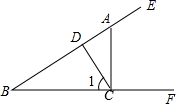 A、① B、①②③ C、①④ D、②③④6. 如图,计划在河边建一水厂,可过C点作CD⊥AB于D点.在D点建水厂,可使水厂到村庄C的路程最短,这样设计的依据是 .
A、① B、①②③ C、①④ D、②③④6. 如图,计划在河边建一水厂,可过C点作CD⊥AB于D点.在D点建水厂,可使水厂到村庄C的路程最短,这样设计的依据是 .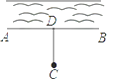 7. 如图,运动会上,小明自踏板M处跳到沙坑P处,甲、乙、丙三名同学分别测得PM=3.25米,PN=3.15米,PF=3.21米,则小明的成绩为 米.(填具体数值)
7. 如图,运动会上,小明自踏板M处跳到沙坑P处,甲、乙、丙三名同学分别测得PM=3.25米,PN=3.15米,PF=3.21米,则小明的成绩为 米.(填具体数值)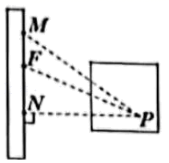 8. 如图,直线AB与CD相交于点O , ,若 ,则 =°.
8. 如图,直线AB与CD相交于点O , ,若 ,则 =°.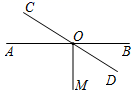 9. 已知直线 与直线 相交于点 , ,垂足为 .若 ,则 的度数为 . (单位用度表示)
9. 已知直线 与直线 相交于点 , ,垂足为 .若 ,则 的度数为 . (单位用度表示)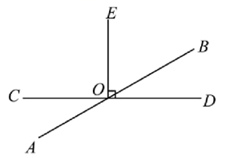 10. 如图,在 的正方形网格中,点 都在格点上,连接 中任意两点得到的所有线段中,与线段 垂直的线段是.
10. 如图,在 的正方形网格中,点 都在格点上,连接 中任意两点得到的所有线段中,与线段 垂直的线段是. 11.
11.如图,CO⊥AB,垂足为O,∠COE﹣∠BOD=4°,∠AOE+∠COD=116°,则∠AOD= .
 12. 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,且∠BON=55°,求∠BOD的度数.
12. 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,且∠BON=55°,求∠BOD的度数.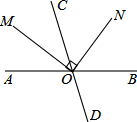 13. 如图,直线AB、CD相交于点O,OE平分∠BOD,OF⊥CD,垂足为O,若∠BOF=38°.
13. 如图,直线AB、CD相交于点O,OE平分∠BOD,OF⊥CD,垂足为O,若∠BOF=38°. (1)、求∠AOC的度数;(2)、过点O作射线OG,使∠GOE=∠BOF,求∠FOG的度数.14. 已知,如图直线 与 相交于点O, ,过点O作射线 , , .
(1)、求∠AOC的度数;(2)、过点O作射线OG,使∠GOE=∠BOF,求∠FOG的度数.14. 已知,如图直线 与 相交于点O, ,过点O作射线 , , . (1)、求 度数;(2)、求 的度数;(3)、直接写出图中所有与 互补的角.
(1)、求 度数;(2)、求 的度数;(3)、直接写出图中所有与 互补的角.二、能力提优
-
15. 下列各项正确的是( )A、有公共顶点且相等的两个角是对顶角 B、过一点有且只有一条直线与已知直线垂直 C、直线外一点到已知直线的垂线段叫做这点到直线的距离 D、同一平面内,两条直线的位置关系只有相交和平行两种16. 如图, 是直线 外一点,从点 向直线 引 , , , 几条线段,其中只有 与 垂直,这几条线段中长度最短的是( )
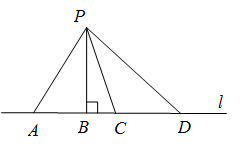 A、 B、 C、 D、17. 如图,点A是直线l外一点,过点A作AB⊥l于点B.在直线l上取一点C,连结AC,使AC=AB,点P在线段BC上,连结AP.若AB=3,则线段AP的长不可能是( )
A、 B、 C、 D、17. 如图,点A是直线l外一点,过点A作AB⊥l于点B.在直线l上取一点C,连结AC,使AC=AB,点P在线段BC上,连结AP.若AB=3,则线段AP的长不可能是( )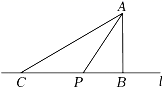 A、3.5 B、4 C、5 D、5.518. 下列说法正确的个数是( )
A、3.5 B、4 C、5 D、5.518. 下列说法正确的个数是( )①射线 与射线 是同一条射线;②点 到点 的距离是线段 ;③画一条长为 的直线;④在同一平面内,过一点有且只有一条直线垂直于已知直线.
A、0个 B、1个 C、2个 D、3个19. 如图,E是直线 上一点, ,射线 平分 , .则 ( ) A、 B、 C、 D、20. 如图, , ,已知 , , ,则点 到直线 的距离是 .
A、 B、 C、 D、20. 如图, , ,已知 , , ,则点 到直线 的距离是 .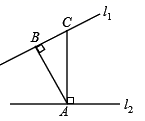 21. 如图,已知 .若 ,则 .
21. 如图,已知 .若 ,则 .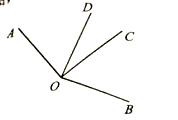 22. 如图,P是直线l外一点,从点P向直线l引PA , PB , PC , PD几条线段,其中只有PA与l垂直. 这几条线段中,最短的是 , 依据是 .
22. 如图,P是直线l外一点,从点P向直线l引PA , PB , PC , PD几条线段,其中只有PA与l垂直. 这几条线段中,最短的是 , 依据是 . 23. 如图,在平面内,两条直线l1 , l2相交于点O,对于平面内任意一点M,若p,q分别是点M到直线l1 , l2 , 的距离,则称(p,q)为点M的“距离坐标”.根据上述规定,“距离坐标”是(3,2)的点共有个.
23. 如图,在平面内,两条直线l1 , l2相交于点O,对于平面内任意一点M,若p,q分别是点M到直线l1 , l2 , 的距离,则称(p,q)为点M的“距离坐标”.根据上述规定,“距离坐标”是(3,2)的点共有个. 24. 如图,点 在直线 上,点 在直线 上,点 到直线 的距离为 ,点 到直线 的距离为 ,线段 的长度为 ,通过测量等方法可以判断在 , , 三个数据中,最大的是 .
24. 如图,点 在直线 上,点 在直线 上,点 到直线 的距离为 ,点 到直线 的距离为 ,线段 的长度为 ,通过测量等方法可以判断在 , , 三个数据中,最大的是 . 25.
25.已知直线AB和CD相交于点O,射线OE⊥AB于O,射线OF⊥CD于O,且∠AOF=25°,求∠BOC与∠EOF的度数.
 26. 如图,直线AB和直线CD交于O点,EO⊥AB,
26. 如图,直线AB和直线CD交于O点,EO⊥AB, (1)、若2∠EOC=∠COB,求∠AOD的度数.(2)、作OF⊥CD,证明:∠EOF=∠COB.27. 如图,已知直线 与 相交于点 为 的角平分线.
(1)、若2∠EOC=∠COB,求∠AOD的度数.(2)、作OF⊥CD,证明:∠EOF=∠COB.27. 如图,已知直线 与 相交于点 为 的角平分线. (1)、求 的度数;(2)、求 的度数.
(1)、求 的度数;(2)、求 的度数.三、延伸拓展
-
28.
如图,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H点的位置,使它到四个村庄距离之和最小;
(2)计划把河水引入蓄水池H中,怎样开渠最短并说明根据.
 29. 已知如图,直线AB、CD相交于点O,∠COE=90°.
29. 已知如图,直线AB、CD相交于点O,∠COE=90°. (1)、若∠AOC=36°,求∠BOE的度数;(2)、若∠BOD:∠BOC=1:5,求∠AOE的度数;(3)、在(2)的条件下,过点O作OF⊥AB,请直接写出∠EOF的度数.30. 已知∠AOB=160°,∠COE是直角,OF平分∠AOE.
(1)、若∠AOC=36°,求∠BOE的度数;(2)、若∠BOD:∠BOC=1:5,求∠AOE的度数;(3)、在(2)的条件下,过点O作OF⊥AB,请直接写出∠EOF的度数.30. 已知∠AOB=160°,∠COE是直角,OF平分∠AOE.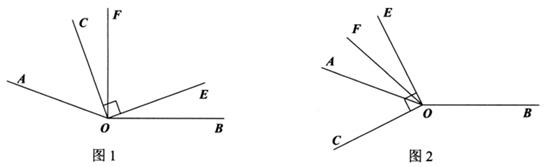 (1)、如图1,若∠COF=32°,则∠BOE=;(2)、如图1,若∠COF=m°,则∠BOE=;∠BOE与∠COF的数量关系为.(3)、在已知条件不变的前提下,当∠COE绕点О逆时针转动到如图2的位置时,第(2)问中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.
(1)、如图1,若∠COF=32°,则∠BOE=;(2)、如图1,若∠COF=m°,则∠BOE=;∠BOE与∠COF的数量关系为.(3)、在已知条件不变的前提下,当∠COE绕点О逆时针转动到如图2的位置时,第(2)问中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.