2022年苏科版初中数学七年级上册 6.3 余角补角对顶角同步练习

试卷更新日期：2022-10-30 类型：同步测试

进入出卷网下载

一、夯实基础

1. 下列图中是对顶角的为（）

A、 B、 C、 D、

查看试题解析
2. 已知∠α＝125°19′，则∠α的补角等于（）

A、144°41′ B、144°81′ C、54°41′ D、54°81′

查看试题解析
3. 如图，点O在直线 $A B$ 上， $∠ C O D = 90 ° ， ∠ A O C = 125 °$ ，则 $∠ B O D$ 的大小为（）

A、 $25 °$ B、 $30 °$ C、 $35 °$ D、 $40 °$

查看试题解析
4. 下列说法正确的是（）

A、锐角的补角不一定是钝角 B、一个角的补角一定大于这个角 C、直角和它的的补角相等 D、锐角和钝角互补

查看试题解析
5. 如图，∠AOD＝∠DOB＝∠COE＝90°，互补的角有（）

A、5对 B、6对 C、7对 D、8对

查看试题解析
6. 如图，已知直线AB与CD相交于点O，OE平分∠AOD，∠EOF＝90°.对于下列结论：①∠BOC＝2∠AOE；②OF平分∠BOD；③∠AOE是∠BOF的余角；④∠AOE是∠COE的补角.其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
7. 如果∠A＝30°，那么∠A的余角为°，∠A的补角为°.

查看试题解析
8. 若 $∠ A = 38 ° 15$ ， $∠ B = 51 ° 45$ ，则 $∠ A$ 与 $∠ B$ 的关系是．（填“互余”或“互补”）

查看试题解析
9. 一个角的余角比它的补角的 $\frac{1}{4}$ 还少 $12 °$ ，则这个角的度数为．

查看试题解析
10. 已知∠1与∠2互余，若∠1=33°27′，则∠2的补角的度数是.

查看试题解析
11. 已知一个角的补角是它余角的3倍，那么这个角等于°．

查看试题解析
12. 如图，直线AB，CD相交于点O， $E O ⊥ A B$ ，垂足为O， $∠ E O C = 35 °$ ，求 $∠ A O D$ 的度数．

查看试题解析
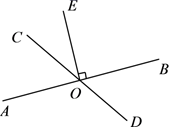13. 如图，点A、O、B在同一条直线上，射线OD平分∠AOC，且∠DOE＝90°．求证：OE平分∠BOC．

查看试题解析
14. 如图， $∠ A O B = 40 °$ ， $O B$ 是 $∠ A O C$ 的平分线， $O D$ 是 $∠ C O E$ 的平分线.

(1)、若 $∠ D O E = 10 °$ ，求 $∠ B O D$ 的度数；

(2)、若 $∠ A O D$ 与 $∠ B O D$ 互补，求 $∠ C O E$ 的度数.

查看试题解析

二、能力提优

15. 下列说法中，正确的是（）

A、一个锐角的补角大于这个角的余角 B、一对互补的角中，一定有一个角是锐角 C、锐角的余角一定是钝角 D、锐角的补角一定是锐角

查看试题解析
16. 已知∠1和∠2互为余角，且∠2与∠3互补，∠1＝60°，则∠3为（）

A、120° B、60° C、30° D、150°

查看试题解析
17. 若 $∠ α = 45 ° - n °$ ， $∠ β = 45 ° + n °$ ，则 $∠ α$ 与 $∠ β$ 的关系是（）

A、互补 B、互余 C、和为钝角 D、和为周角

查看试题解析
18. ∠α与∠β的度数分别是 2m−67和 68−m，且∠α与∠β都是∠γ 的补角，那么∠α与∠β的关系是（）

A、互余但不相等 B、相等但不互余 C、互为补角 D、互余且相等

查看试题解析
19. 如图，点A，O，B在一条直线上，OE⊥AB于点O，如果∠1与∠2互余，那么图中相等的角有（）

A、6对 B、5对 C、4对 D、3对

查看试题解析
20. 已知 $∠ α$ 与 $∠ β$ 满足 $2 ∠ α + 3 ∠ β = 180^{°}$ ，下列式子表示的角：① $90^{°} - ∠ β$ ：② $30^{°} + \frac{3}{2} ∠ α$ ；③ $∠ α + \frac{1}{2} ∠ β$ ；④ $2 ∠ α + ∠ β$ 中，其中是 $∠ β$ 的余角的是（）

A、①② B、①③ C、②④ D、③④

查看试题解析
21. 已知∠α与∠β互余，且∠α=40°，则∠β的度数为．

查看试题解析
22. 若一个角度数是115°6′，则这个角的补角是．

查看试题解析
23. 已知∠α和∠β互为补角，并且∠β的一半比∠α小30°，则∠α＝， ∠β＝．

查看试题解析
24. 若 $∠ α$ 与 $∠ β$ 互余，且 $∠ α ： ∠ β = 2 ： 3$ ，则 $\frac{2}{3} ∠ α + \frac{5}{6} ∠ β =$ ．

查看试题解析
25. 如图，已知点 $A$ 是射线 $B E$ 上一点，过 $A$ 作 $C A ⊥ B E$ 交射线 $B F$ 于点 $C$ ， $A D ⊥ B F$ 交射线 $B F$ 于点 $D$ ，给出下列结论：① $∠ 1$ 是 $∠ B$ 的余角；②图中互余的角共有3对；③ $∠ 1$ 的补角只有 $∠ A C F$ ；④与 $∠ A D B$ 互补的角共有3个，其中正确结论有（把你认为正确的结论的序号都填上）.

查看试题解析
26. 如图，OB 是∠AOC的平分线，OD是∠COE的平分线．

(1)、若∠AOB=40°，∠DOE=36°，求∠BOD的度数；

(2)、若∠AOD与∠BOD互补，且∠DOE=30°，求∠AOB的度数．

查看试题解析
27. 如图， $∠ A O B = ∠ D O C = 90 °$ ．

(1)、试说明∠AOD与∠BOC互补；

(2)、如图2，当射线OA、OB都在∠COD的外部时，过点O作射线OE、OF，若射线OE是∠BOE的三等分线（ $∠ B O E < ∠ C O E$ ）， $∠ D O F = 2 ∠ A O F$ ，求 $∠ E O F$ 的度数：

(3)、如图3，在（2）的条件下， $∠ A O F = ∠ B O C + ∠ C O E$ ，射线OM平分∠EOD，过点O作射线ON，使 $∠ F O N ： ∠ F O M = 2 ： 5$ ，求 $∠ A O N$ 的度数．

查看试题解析
28. 在同一平面内已知∠AOB＝150°，∠COD＝90°，OE平分∠BOD ．

(1)、当∠COD的位置如图1所示时，且∠EOC＝35°，求∠AOD的度数；

(2)、当∠COD的位置如图2所示时，作∠AOC的角平分线OF ，求∠EOF的度数；

(3)、当∠COD的位置如图3所示时，若∠AOC与∠BOD互补，请你过点O作射线OM ，使得∠COM为∠AOC的余角，并求出∠MOE的度数．（题中的角都是小于平角的角）

查看试题解析

三、延伸拓展

29. 如图，按照上北下南，左西右东的规定画出方向十字线，∠AOE＝m°，∠EOF＝90°，OM、ON分别平分∠AOE和∠BOF，下面说法：
①点E位于点O的北偏西m°；②图中互余的角有4对；③若∠BOF＝4∠AOE，则∠DON＝54°；④若 $\frac{∠ M O N}{∠ A O E + ∠ B O F} = n$ ，则n的倒数是 $\frac{2}{3}$ ，其中正确有（）

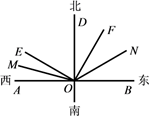A、3个 B、2个 C、1个 D、0个

查看试题解析
30. 如图1，已知∠AOC＝140°，∠BOC的余角比它的补角的 $\frac{1}{2}$ 少 $10^{\circ}$ .

(1)、求∠BOC的度数；

(2)、如图1，当射线OP从OB处绕点O以4度/秒的速度逆时针旋转，在旋转过程中，保持射线OP始终在∠BOA的内部，当∠POC＝10°时，求旋转时间.

(3)、如图2，若射线OD为∠AOC的平分线，当射线OP从OB处绕点O以4度/秒的速度逆时针旋转，同时射线OT从射线OD处以x度/秒的速度绕点O顺时针旋转，当这两条射线重合于射线OE处（OE在∠DOC的内部）时， $\frac{∠ D O E + ∠ B O C}{∠ C O E} = \frac{7}{2}$ ，求x的值.
（注：本题中所涉及的角都是小于 $180^{\circ}$ 的角）

查看试题解析

2022年苏科版初中数学七年级上册 6.3 余角 补角 对顶角 同步练习

一、夯实基础

二、能力提优

三、延伸拓展

2022年苏科版初中数学七年级上册 6.3 余角补角对顶角同步练习