2022年苏科版初中数学七年级上册 6.2 角 同步练习
试卷更新日期：2022-10-30 类型：同步测试
一、夯实基础
-
1. 若∠α＝5.12°，则∠α用度、分、秒表示为（ ）A、5°12′ B、5°7′12″ C、5°7′2″ D、5°10′2″2. 关于角的描述不正确的是（ ）
A、∠1与∠AOB表示同一个角 B、∠AOC可以用∠O表示 C、∠AOC＝∠AOB+∠BOC D、∠β表示∠BOC3. 下列各角中，为锐角的是（ ）A、 平角 B、 周角 C、 直角 D、 周角4. 在灯塔P处观测到轮船A位于北偏西55°的方向，同时轮船B在南偏东15°的方向，那么∠AOB的大小为（ ）
A、100° B、105° C、125° D、140°5. 如图，OC平分∠AOD，OD平分∠BOC，下列等式不成立的是（ ）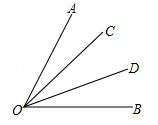
A、∠AOC=∠BOD B、∠COD= ∠AOB C、∠AOC= ∠AOD D、∠BOD= ∠BOC6. 已知 ， 比较这两个角的大小， 结果为∠1∠2.7. 计算：35.1°＋40.5°＝ ． （结果用度表示）8. 钟表上显示8：30，时针与分针的夹角为 。9. 已知∠AOB=3∠BOC，射线OD平分∠AOC，若∠BOD=30°，则∠BOC的度数为.10. 如图，∠AOC与∠BOC的度数比为5：2，OD平分∠AOB，若∠COD＝15°，求∠AOB的度数.
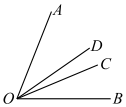11. 如图，∠AOB是平角， ， ，OM、ON外别是∠AOC、∠BOD的平分线，求∠MON的度数.
12. 如图，AB为一条直线，OC是∠AOD的平分线.
(1)、如图①，若∠COE为直角，且∠AOD＝70°，求∠BOE的度数；(2)、如图②，若∠DOE：∠BOD＝2：5，且∠COE＝80°，求∠BOE的度数.二、能力提优
-
13. 下列图形中，能用 ， ， 三种方法表示同一个角的是（ ）A、
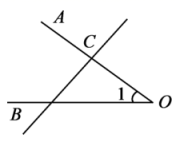B、
C、
D、
14. 如图，∠AOE＝100°，∠BOF＝80°，OE平分∠BOC，OF平分∠AOC，则∠EOF的度数为（ ）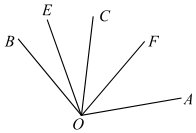
A、40° B、50° C、60° D、70°15. 已知∠AOB＝100°，过点O作射线OC、OM，使∠AOC＝20°，OM是∠BOC的平分线，则∠BOM的度数为（ ）A、60° B、60°或40° C、120°或80° D、40°16. 如图， ，射线OM、ON分别平分 与 ， 是直角，则 的度数为（ ）
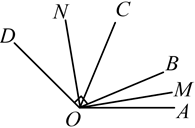A、70° B、62° C、60° D、58°17. 用一副三角板（两块，可以组合）画角，不可能画出的角的度数是（ ）A、 B、 C、 D、18. 如图，点O为直线AB上一点，为直角，OE平分 ， OF平分 ， OG平分 ． 下列结论：①；②；③；④ ． 正确的有（ ）
A、4个 B、3个 C、2个 D、1个19. 将一副三角板如图①的位置摆放，其中30°直角三角板的直角边与等腰直角三角板的斜边重合，30°直角三角板直角顶点与等腰直角三角板的锐角顶点重合（为点O）．现将30°的直角三角板绕点O顺时针旋转至如图②的位置，此时为25°，则（ ）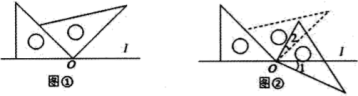
A、15° B、20° C、25° D、30°20. 计算：18°29′+39°47′＝.21. 钟面上4时30分，时针与分针的夹角是度，15分钟后时针与分针的夹角是度.22. 已知 ， ， OD平分∠AOB，OM平分∠AOC，则∠MOD的度数是 ．23. 已知∠AOB=40°，其平分线是OD，自O点引射线OC，若∠AOC：∠COB=2：3则∠COD= ．24. 如图，将一副三角板摆放在直线AB上， ， ，设 ，则用x的代数式表示 的度数为.
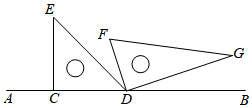25. 如图， 是 内的两条射线， 平分 ， ，若 ， ，求 的度数.
26. 如图，点O为直线AB上一点， ，OD平分 .
(1)、求 的度数：(2)、作射线OE，使 ，求 的度数.27. 已知，O是直线AB上的一点，OC⊥OE．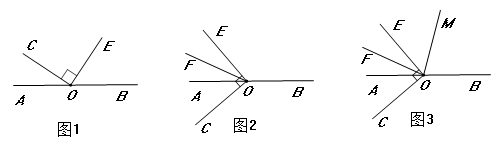
(1)、如图①，若∠COA＝34°，求∠BOE的度数．(2)、如图②，当射线OC在直线AB下方时，OF平分∠AOE，∠BOE＝130°，求∠COF的度数．(3)、在（2）的条件下，如图③，在∠BOE内部作射线OM，使∠COM+∠AOE＝2∠BOM+∠FOM，求∠BOM的度数．三、延伸拓展
-
28. 如图，点C，D在线段BE上（C在D的左侧），点A在线段BE外，连接AB，AC，AD，AE，已知∠BAE ＝ 120°，∠CAD ＝ 60°，有下列说法：①直线CD上以B，C，D，E为端点的线段共有6条；②作∠BAM＝ ∠BAD，∠EAN＝ ∠EAC.则∠MAN＝30°；③以A为顶点的所有小于平角的角的度数和为420°；④若BC＝2，CD＝DE＝3，点F是线段BE上任意一点，则点F到点B，C，D，E的距离之和最大值为17，最小值为11.其中说法正确的有 .（填上所有正确说法的序号）
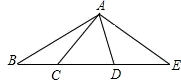29. （问题回顾）我们曾解决过这样的问题：如图1，点O在直线 上， ， 分别平分 ， ，可求得 .（不用求解）
（问题改编）
点O在直线 上， ，OE平分 .
(1)、如图2，若 ，求 的度数；(2)、将图2中的 按图3所示的位置进行放置，写出 与 度数间的等量关系，并写明理由.30. 如图，∠AOB＝90°，∠COD＝60°．
(1)、若OC平分∠AOD，求∠BOC的度数；(2)、若∠BOC＝∠AOD，求∠AOD的度数；(3)、若同一平面内三条射线OT、OM、ON有公共端点O，且满足∠MOT＝∠NOT或者∠NOT＝∠MOT，我们称OT是OM和ON的“和谐线”．若射线OP从射线OB的位置开始，绕点O按逆时针方向以每秒12°的速度旋转，同时射线OQ从射线OA的位置开始，绕点O按顺时针方向以每秒9°的速度旋转，射线OP旋转的时间为t（单位：秒），且0＜t＜15，求当射线OP为两条射线OA和OQ的“和谐线”时t的值．