山西省长治市长子县2020-2021学年八年级上学期期末数学试题

试卷更新日期：2022-10-28 类型：期末考试

进入出卷网下载

一、单选题

1. 已知一个数的平方根是 $\pm 3$ ，这个数是（）

A、 $- 9$ B、9 C、81 D、 $\pm \sqrt{3}$

查看试题解析
2. 下列运算正确的是（）

A、(－2a)²＝－4a² B、a⁸÷a²＝a⁴ C、(a⁵)²＝a⁷ D、(－a＋2)(－a－2)＝a²－4

查看试题解析
3. 如图，一只电子蚂蚁从正方体的顶点A处沿着表面爬到顶点C处，电子蚂蚁的部分爬行路线在平面展开图中的表示如图的虚线，其中能说明爬行路线最短的是（）

A、 B、 C、 D、

查看试题解析
4. 若 $\frac{(1 0^{2} - 1) (1 2^{2} - 1)}{k} = 9 \times 11 \times 13$ ，则 $k =$ （）

A、12 B、11 C、10 D、9

查看试题解析
5. 某班级组织活动，为了解同学们喜爱的体育运动项目，设计了如图尚不完整的调查问卷：
准备在“①室外体育运动，②篮球，③足球，④游泳，⑤球类运动”中选取三个作为该调查问卷问题的备选项目，选取合理的是（）

A、①②③ B、①③⑤ C、②③④ D、②④⑤

查看试题解析
6. 按如图所示的程序计算，若开始输入的值为25，则最后输出的y值是（）

A、 $\sqrt{5}$ B、 $\pm \sqrt{5}$ C、5 D、 $\pm 5$

查看试题解析
7. 如图，根据图中尺规作图痕迹，计算 $∠ 1$ 的度数是（）

A、 $22 °$ B、 $32 °$ C、 $34 °$ D、 $68 °$

查看试题解析
8. 如图，OC是∠AOB的平分线，P是OC上一点，P点到OA的距离PE＝2，点F是OB上任意一点，则线段PF的长的取值范围是（　　）

A、PF＜2 B、PF＞2 C、PF≥2 D、PF≤2

查看试题解析
9. 如图， $△ A B C$ 是等边三角形， $A D$ 是 $B C$ 边上的中线，点E在 $A D$ 上，且 $D E = \frac{1}{2} B C$ ，则 $∠ A F E =$ （）

A、100° B、105° C、110° D、115°

查看试题解析
10. 勾股定理是人类最伟大的科学发明之一．如图1，以直角三角形ABC的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大的正方形内，三个阴影部分面积分别记为S₁ ， S₂ ， S₃ ，若已知S₁＝2，S₂＝5，S₃＝8，则两个较小正方形纸片的重叠部分（四边形DEFG）的面积为（）

A、7 B、10 C、13 D、15

查看试题解析

二、填空题

11. 如图，数轴上点A，B对应的数分别为 $- 2$ ， 1，点C在线段 $A B$ 上运动．请你写出点C可能对应的一个无理数是．

查看试题解析
12. 若2ⁿ+2ⁿ+2ⁿ+2ⁿ=2⁸ ，则n=.

查看试题解析
13. 某校八年级（1）班团支部为了让同学们进一步了解中国科技的发展，给班上同学布置了一项课外作业，从选出的以下五个内容中任选一个内容进行手抄报的制作．A．“北斗卫星”；B．“5G时代”；C．“智轨快运系统”；D．“东风快递”；E．“高铁”．统计同学们所选内容的频数，绘制如图所示的折线统计图，则选“5G时代”的频率为．

查看试题解析
14. 如图，山坡上，树甲从点A处折断，其树顶恰好落在另一棵树乙的根部C处，已知AB＝4m，BC＝10m，已知两棵树的水平距离为6m，则树甲原来高．

查看试题解析
15. 如图，G、H分别是四边形ABCD的边AD、AB上的点，∠GCH=45°，CD=CB=2，∠D=∠DCB=∠B=90°，则△AGH的周长为.

查看试题解析

三、解答题

16.

(1)、计算： $\sqrt[3]{- 27} + | \sqrt{3} - 2 | - \sqrt{\frac{9}{4}}$ ；

(2)、因式分解：﹣mx²+2mxy﹣my² ．

查看试题解析
17. 先化简，再求值：[（x+2y）² +（ x+2y）（ x-2y）]÷2x ，其中x=－3，y=－2.

查看试题解析
18.

(1)、填空： $\sqrt{0.0001}$ ＝0.01， $\sqrt{0.01}$ ＝， $\sqrt{1}$ ＝1， $\sqrt{100}$ ＝10， $\sqrt{10000}$ ＝， …

(2)、观察上述求算术平方根的规律，并利用这个规律解决下列问题：
①已知 $\sqrt{10}$ ≈3.16，则 $\sqrt{1000}$ ≈；
②已知 $\sqrt{3.68}$ ≈1.918， $\sqrt{a}$ ≈191.8，则a＝．

(3)、根据上述探究过程类比一个数的立方根：已知 $\sqrt[3]{2}$ ≈1.26， $\sqrt[3]{m}$ ≈12.6，则m＝．

查看试题解析

19. 如图1是某学校的篮球架实物图，其侧面示意图如图2所示，“综合与实践”小组开展了测量篮板

A B

长度的实践活动．在不便于直接测量的情况下，“综合与实践”小组设计了如下方案：

课题	测量篮板的长度
成员	组长：xxx 组员：xxx ， xxx ， xxx
工具	竹竿，皮尺，计算器等
测量示意图		说明： $A B$ 垂直于地面于点 $C$ ，线段 $A D$ ， $B E$ 表示同一根竹竿，第一次将竹竿的一个端点与点 $A$ 重合，另一端点落在地面的点 $D$ 处，第二次将竹竿的一个端点与点 $B$ 重合，另一端点落在地面的点 $E$ 处．
测量数据	测量项目	数值
	竹竿的长度	5米
	$C D$ 的长度	3.062米
	$C E$ 的长度	4.073米
参考数值	${13.062}^{2} \approx 9.376$ ， ${4.073}^{2} \approx 16.589$ ， $\sqrt{15.624} \approx 3.952$ ， $\sqrt{8.411} \approx 2.900$

根据以上测量结果，请你帮助该“综合与实践”小组求出学校篮板 $A B$ 的长度（结果精确到0.01米）．

查看试题解析

20. 如今很多人都是“手机不离手．疫情发生以来，有的人手机使用时间比以前更长了，也有人养成了健康有节律的手机使用习惯．近日，中国青年报社对中学生、大学生和上班族进行了一项抽样调查，记者李斌把调查结果绘制成如下统计图：
每天使用手机时长情况统计图（1）

每天使用手机时长情况统计图（2）

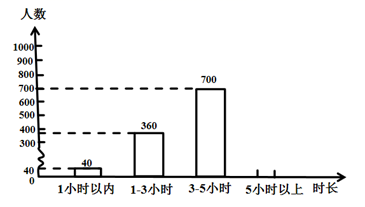(1)、结合两个统计图中的数据，可算出接受调查的一共有人．

(2)、每天使用手机 $5$ 小时以上的占全部受调查人数的 $%$ ，是人．

(3)、88.5%的受调查者坦言：最近手机使用时间增长了，主要用手机刷短视频、上网课和沟通工作．由于长时间观看手机屏幕会使眼睛疲劳、干涩，引发视力下降，所以养成健康、自律的手机使用意识和习惯很重要．对此你有什么好的建议？（至少写出两条）

查看试题解析
21. 如图1，AD为△ABC的中线，延长AD至E，使DE＝AD．

(1)、试证明：△ACD≌△EBD；

(2)、用上述方法解答下列问题：如图2，AD为△ABC的中线，BMI交AD于C，交AC于M，若AM＝GM，求证：BG＝AC．

查看试题解析
22. 我们将（a+b）²＝a²+2ab+b²进行变形，如：a²+b²＝（a+b）²﹣2ab，ab＝ $\frac{(a + b)^{2} - (a^{2} + b^{2})}{2}$ 等．根据以上变形解决下列问题：

(1)、已知a²+b²＝8，（a+b）²＝48，则ab＝．

(2)、已知，若x满足（25﹣x）（x﹣10）＝﹣15，求（25﹣x）²+（x﹣10）²的值．

(3)、如图，四边形ABED是梯形，DA⊥AB，EB⊥AB，AD＝AC，BE＝BC，连接CD，CE，若AC•BC＝10，则图中阴影部分的面积为．

查看试题解析
23.

(1)、如图①，D是等边△ABC的边BA上一动点（点D与点B不重合），连接DC，以DC为边，在BC上方作等边△DCF，连接AF，你能发现AF与BD之间的数量关系吗？并证明你发现的结论；

(2)、如图②，当动点D运动至等边△ABC边BA的延长线时，其他作法与（1）相同，猜想AF与BD在（1）中的结论是否仍然成立？若成立，请证明；

(3)、Ⅰ.如图③，当动点D在等边△ABC边BA上运动时（点D与B不重合），连接DC，以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′，连接AF，BF′，探究AF，BF′与AB有何数量关系？并证明你的探究的结论；
Ⅱ.如图④，当动点D在等边△ABC的边BA的延长线上运动时，其他作法与图③相同，Ⅰ中的结论是否成立？若不成立，是否有新的结论？并证明你得出的结论.

查看试题解析