山西省吕梁市交口县2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-10-28 类型：期末考试

进入出卷网下载

一、单选题

1. 冬季奥林匹克运动会是世界规模最大的冬季综合性运动会，每四年举办一次，第24届冬奥会将于2022年在北京和张家口举办．下列四个图分别是第24届冬奥会图标中的一部分，其中是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、 $x^{2} + x = x^{3}$ B、 $x^{2} \cdot x^{3} = x^{5}$ C、 ${(x^{2})}^{3} = x^{5}$ D、 $x^{2} + x^{3} = 5 x$

查看试题解析
3. 如图，在Rt△ABC中，∠C=90°，AD是∠BAC平分线，DE⊥AB，垂足为E，若CD=10，则DE的长度为（）

A、 $10$ B、 $6$ C、 $4$ D、 $2$

查看试题解析
4. 下列式子是分式的是（）

A、 $\frac{a - b}{2}$ B、 $\frac{5 + y}{π}$ C、 $\frac{x + 3}{x}$ D、1＋x

查看试题解析
5. 如图，已知 $△ A B C ≌ △ A D E$ ，若 $∠ E = 70 °$ ， $∠ D = 30 °$ ，则 $∠ B A C$ 的度数是（）

A、 $80 °$ B、 $70 °$ C、 $40 °$ D、 $30 °$

查看试题解析
6. 若点A（﹣3，a）与B（b ， 2）关于x轴对称，则点M（a ， b）所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 如图，已知OC平分∠AOB，CD//OB，若OD=3cm，则CD等于（）

A、1.5cm B、2cm C、3cm D、4cm

查看试题解析
8. 因式分解a²b﹣2ab＋b正确的是（）

A、b（a²﹣2a） B、ab（a﹣2） C、b（a²﹣2a＋1） D、b（a﹣1）²

查看试题解析
9. 瓜达尔港是我国实施“一带一路”战略构想的重要一步，为了增进中巴友谊，促进全球经济一体化发展，我国施工队预计把距离港口420km的普通公路升级成同等长度的高速公路，升级后汽车行驶的平均速度比原来提高50％，行驶时间缩短2h，那么汽车原来的平均速度为（）

A、80km/h B、75km/h C、70km/h D、65km/h

查看试题解析
10. 如图，等边三角形ABC与互相平行的直线a，b相交，若∠1=25°，则∠2的大小为（）

A、25° B、35° C、45° D、55°

查看试题解析

二、填空题

11. 分式 $\frac{1}{3 x^{2} y^{2}}$ 和 $\frac{1}{4 x y^{3}}$ 的最简公分母是.

查看试题解析
12. 设 $(2 a + b)^{2} = (2 a - b)^{2} + A$ ，则A= ．

查看试题解析
13. 清代袁枚的诗《苔》中有这样的诗句：“苔花如米小，也学牡丹开”．据了解苔花的花粉直径大约仅有0.00000084米，该数据用科学记数法可表示为．

查看试题解析
14. 如图，用一条宽度相等的足够长的纸条打一个结（如图1），然后轻轻拉紧、压平就可以得到如图2所示的正五边形 $A B C D E$ .在图2中， $∠ A C D$ 的度数为.

查看试题解析
15. 一个等边三角形，一个直角三角形以及一个等腰三角形如图放置，等腰三角形的底角∠3＝80°，则∠1+∠2＝．

查看试题解析

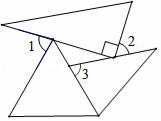
三、解答题

16.

(1)、计算： $7 m {(4 m^{2} p)}^{2} \div 7 m^{2}$

(2)、解分式方程： $\frac{x}{x - 2} - 1 = \frac{1}{x^{2} - 4}$

查看试题解析
17. 如图①、图②、图③都是 $3 \times 3$ 的正方形网格，每个小正方形的顶点称为格点．A， $B$ ，C均为格点．在给定的网格中，按下列要求画图：

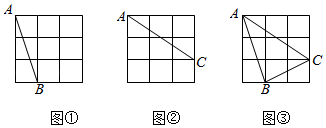(1)、在图①中，画一条不与 $A B$ 重合的线段 $M N$ ，使 $M N$ 与 $A B$ 关于某条直线对称，且M，N为格点．

(2)、在图②中，画一条不与 $A C$ 重合的线段 $P Q$ ，使 $P Q$ 与 $A C$ 关于某条直线对称，且P，Q为格点．

(3)、在图③中，画一个 $Δ D E F$ ，使 $Δ D E F$ 与 $Δ A B C$ 关于某条直线对称，且D，E，F为格点．

查看试题解析
18. 如图，现有一块长为（4a+b）米，宽为（a+2b）米的长方形地块，规划将阴影部分进行绿化，中间预留部分是边长为a米的正方形.

(1)、求绿化的面积S（用含a，b的代数式表示，并化简）；

(2)、若a=2，b=3，绿化成本为100元/平方米，则完成绿化共需要多少元？

查看试题解析
19. 如图，等边△ABC中，D是AC的中点，E是BC延长线上的一点，且CE=CD，DF⊥BE，垂足是F，求证：BF=EF．

查看试题解析
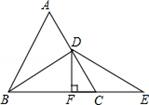20. 阅读以下材料，并解决问题：
常用的分解因式的方法有提取公因式法、公式法等，但有的多项式则不能直接用上述两种方法进行分解，比如多项式． $x^{2} - 4 y^{2} - 2 x + 4 y$ ．这样我们就需要结合式子特点，探究新的分解方法．仔细观察这个四项式，会发现：若把它的前两项结合为一组符合平方差公式特点，把它的后两项结合为一组可提取公因式，而且对前后两组分别进行因式分解后会出现新的公因式，提取新的公因式就可以完成对整个式子的因式分解．具体过程如下：
例1： $x^{2} - 4 y^{2} - 2 x + 4 y$
$= (x^{2} - 4 y^{2}) - (2 x - 4 y)$ ……………………分成两组
$= (x + 2 y) (x - 2 y) - 2 (x - 2 y)$ ………………分别分解
$= (x - 2 y) (x + 2 y - 2)$ ………………………提取公因式完成分解
像这种将一个多项式适当分组后，进行分解因式的方法叫做分组分解法．分组分解法一般是针对四项或四项以上的多项式，关键在恰当分组，分组须有“预见性”，预见下一步能继续分解，直到完成分解．

(1)、材料例1中，分组的目的是．

(2)、若要将以下多项式进行因式分解，怎样分组比较合适？
$x^{2} - y^{2} + x + y =$ ；
$2 a + a^{2} - 2 b - 2 a b + b^{2} =$ ．

(3)、利用分组分解法进行因式分解： $x^{2} - 2 x y + y^{2} - 4$ ．

查看试题解析
21. 为了进一步落实教育部《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》精神，某作文培训机构积极响应号召，助力“双减”真正落地，成功转型为读书吧．吧主计划购买若干套“四大名著”来充实书吧．第一次用3600元购买的图书满足不了学生的阅读需求，第二次购买时正赶上图书城8折优惠，用2400元购买的套数只比第一次少4套．求第一次购进的“四大名著”每套的价格是多少元？

查看试题解析
22. 如图，直线 $m$ 是 $△ ABC$ 中BC边的垂直平分线，点P是直线m上的一动点，若 $A B = 6$ ， $A C = 4$ ， $B C = 7$ ．

(1)、求 $P A + P B$ 的最小值，并说明理由．

(2)、求 $△ A P C$ 周长的最小值．

查看试题解析
23. 【阅读理解】
课外兴趣小组活动时，老师提出了如下问题：
如图1，△ABC中，若AB＝8，AC＝6，求BC边上的中线AD的取值范围.小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE＝AD，请根据小明的方法思考：

(1)、由已知和作图能得到△ADC≌△EDB的理由是____.

A、SSS B、SAS C、AAS D、HL

(2)、求得AD的取值范围是____.

A、6＜AD＜8 B、6≤AD≤8 C、1＜AD＜7 D、1≤AD≤7

(3)、【感悟】
解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中.
【问题解决】
如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AE＝EF.求证：AC＝BF.

查看试题解析