山西省晋中市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-10-28 类型：期末考试

进入出卷网下载

一、单选题

1. 实数 $\sqrt{3}$ 的倒数是（）

A、 $- \sqrt{3}$ B、 $\pm \sqrt{3}$ C、 $\frac{1}{3}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
2. 我国是最早了解勾股定理的国家之一．早在三千多年前，周朝数学家商高就提出，将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”．它被记载于下列哪部著名数学著作中（　　）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（　　）

A、 $\sqrt{2} + \sqrt{7} = 3$ B、 $\sqrt{5} - \sqrt{2} = \sqrt{3}$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{8} \div \sqrt{2} = 4$

查看试题解析
4. 如图，在 4×4 的正方形网格中（每个小正方形边长均为 1），点A，B，C 在格点上，连接 AB，AC，BC，则△ABC 的形状是（　　）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法确定

查看试题解析
5. 某社区计划组织以“全民健身，‘毽’步如飞”为主题的踢毽子比赛活动，为了了解参赛成员踢毽子水平及稳定程度，在比赛前期甲、乙、丙、丁四名参赛成员分别记录了自己在规定时间内 5 次踢毽子的数量，并计算出了各自的平均个数 $\bar{x}$ 及方差S² ，如下表所示：

甲
乙
丙
丁
$\bar{x}$
90
103
95
108
S²
$\frac{26}{5}$
$\frac{18}{5}$
12
$\frac{18}{5}$
根据参赛成员踢毽子的平均数量及稳定程度，你认为哪位参赛成员获胜的可能性大（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 据史书记载，漏刻是中国古代的一种计时工具，是古代人民对函数思想的创造性应用．研究发现水位 h（cm）与时间 t（min）满足 h=0.4t+2，当 h 为 6cm时，时间 t 的值为（）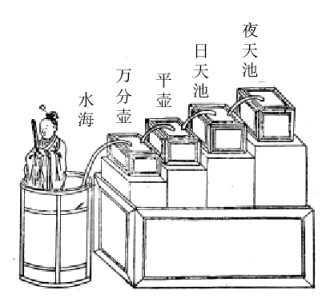

A、4.4min B、10min C、15min D、20min

查看试题解析
7. 如图是一只蝴蝶标本，已知表示蝴蝶两“翅膀尾部”A，B 两点的坐标分别为（－2，－3），（2，－3），则表示蝴蝶身体“尾部”C 点的坐标为（）

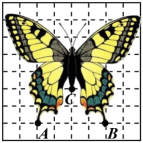A、（0，－1） B、（1，－1） C、（－1，0） D、（2，－1）

查看试题解析
8. 如图，已知 AB∥CD，点 F，G 分别在直线 AB，CD 上，∠BFE 的平分线 FQ 所在直线与∠CGE 的平分线相交于点 P，若∠BFE=50°，∠CGE=140°，则∠GPQ 的度数为（　　）

A、30° B、40° C、45° D、50°

查看试题解析
9. 为预防新冠疫情，民生大院入口的正上方 A 处装有红外线激光测温仪（如图所示），测温仪离地面的距离 AB＝2.4 米，当人体进入感应范围内时，测温仪就会自动测温并报告人体体温.当身高为 1.8 米的市民 CD 正对门缓慢走到离门 0.8 米的地方时（即 BC＝0.8 米），测温仪自动显示体温，则人头顶离测温仪的距离 AD 等于（　　）

A、1.0 米 B、1.2 米 C、1.25 米 D、1.5 米

查看试题解析
10. 甲、乙两个草莓采摘园为吸引顾客，在草莓销售价格相同的基础上分别推出优惠方案，甲园：顾客进园需购买门票，采摘的草莓按六折优惠．乙园：顾客进园免门票，采摘草莓超过一定数量后，超过的部分打折销售．活动期间，某顾客的草莓采摘量为x千克，若在甲园采摘需总费用y₁元，若在乙园采摘需总费用y₂元．y₁ ， y₂与x之间的函数图象如图所示，则下列说法中错误的是（　　）

A、甲园的门票费用是60元 B、草莓优惠前的销售价格是40元/千克 C、乙园超过5千克后，超过的部分价格优惠是打五折 D、若顾客采摘15千克草莓，那么到甲园比到乙园采摘更实惠

查看试题解析

二、填空题

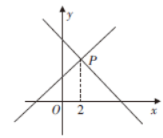
11. 计算 $(\sqrt{5} + \sqrt{3}) (\sqrt{5} - \sqrt{3})$ 的结果等于．

查看试题解析
12. 如图，已知函数 $y = x + 3$ 和 $y = a x + 7$ 的图象交于点P，点P的横坐标为2，则关于x，y的方程组 ${\begin{array}{l} x - y = - 3 \\ a x - y = - 7 \end{array}$ 的解是．

查看试题解析
13. 某超市决定招聘一名广告策划人员，小强参与应聘并通过测试取得三项成绩如下表：
测试项目
创新能力
专业知识
语言表达
测试成绩/分
70
90
80
将创新能力、专业知识和语言表达三项测试成绩按 5：3：2 的比例计入总成绩，则小强的总成绩是分．

查看试题解析
14. 塑料凳子轻便实用，人们生活中随处可见．如图，3 支塑料凳子叠放在一起的高度为55cm，5 支塑料凳子叠放在一起的高度为 65cm，当有 10 支塑料凳子整齐地叠放在一起时，其高度是cm．

查看试题解析
15. 如图，长方形 ABCO 的边 AO，CO 正好落在坐标轴上，且 AB=4，OA=2，点 D 是线段 OC 上一点，点 E 为线段 AB 上一点，沿 DE 折叠，使点 B 与点 O 重合，点 C 落到 C＇处，则此时点 D 的坐标为．

查看试题解析

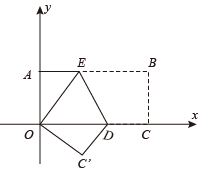
三、解答题

16. 计算：

(1)、 $\sqrt{12} + \sqrt[3]{- 8} + (- \sqrt{2})^{2}$

(2)、 $\frac{\sqrt{8} + \sqrt{18}}{\sqrt{2}} - \sqrt{\frac{9}{24}} \times \sqrt{6}$

查看试题解析
17. 下面是小明同学解二元一次方程组的过程，请你阅读并完成相应的任务：
解方程组： ${\begin{array}{l} 3 x + 4 y = 5 ① \\ x - 2 y = 4 ② \end{array}$
解：②× 2  ，得2x－4y=4  ③…………………………………第一步
①+③，得5x=9 …………………………………第二步
$x = \frac{9}{5}$ …………………………………第三步
把 $x = \frac{9}{5}$ 代入②，得 y= $- \frac{11}{10}$ …………………………………第四步
∴原方程组的解为 ${\begin{array}{l} x = \frac{9}{5} \\ y = - \frac{11}{10} \end{array}$ …………………………………第五步
任务一：
①上述材料中小明同学解二元一次方程组的数学方法是（填序号即可）；
A.公式法    B.换元法    C.代入法    D.加减法
②上述材料中第二步和第四步的基本思想是“消元”，即把“二元”变“一元”，在此过程中体现的数学思想是（填序号即可）；
A.转化    B.公理化    C.演绎    D.数形结合
③第步开始出现错误，这一步错误的原因是；

查看试题解析
18. 如图，点 A，B，C，D 在同一条直线上，且 AB=CD，请从以下三个条件：①AE∥DF；②AE=DF；③EC=FB 中，再选两个作为已知条件，另一个作为结论，推出一个正确的命题，并证明这个命题．
已知：AB=CD，，；
求证：．（填写序号即可）
证明：

查看试题解析

19. 为落实“双减”政策，满足学生课后延时服务需求，某校以课后服务“5+2”的模式全面开展内容丰富、形式多样的活动，切实减轻学生学习负担，促进学生健康成长．为了了解八年级学生延时时间范围内的体育活动情况，某调查小组随机从八年级学生中抽取了 30 名男同学，20 名女同学进行了为期一周的跟踪调查，调查结果如表所示：

性别	平均每天参加体育活动达到1 小时的人数	平均每天参加体育活动不达1 小时的人数	合计
男生	25	5	30
女生	11	m	20
合计	36	14	50

对平均每天参加体育活动达到 1 小时的男生和女生进行深入调查，发现他们分别在一周内参加各项体育活动的时间不等，根据调查数据绘制了以下折线统计图：

一周内参加各项体育活动时间折线统计图

(1)、填空：m 的值为；

(2)、根据上述统计图表填写下表中的相关统计量：

年级	参加各项体育活动时间的中位数	参加各项体育活动时间的方差
男生		54.4
女生	11

(3)、请你对所在学校落实国家“双减政策”采取的措施，写出一条合理的评价或建议．

查看试题解析

20. 太原南铁路客运站，是山西省内第一座高标准现代化的大型铁路客运站，太原市标志性建筑之一．如图 1，站内出入口设有上、下行自动扶梯和步行楼梯，小颖和爸爸从站内二层扶梯口同时下行去一层出口，爸爸乘自动扶梯，小颖走步行楼梯，爸爸离一层出口地面的高度 h（单位：m）与下行时间 x（单位：s）之间具有函数关系 $h = - \frac{2}{5} x + 6$ ，小颖离一层出口地面的高度 y（单位：m）与下行时间 x（单位：s）的函数关系如图 2 所示．

(1)、如图 2，求 y 关于 x 的函数表达式；

(2)、爸爸乘自动扶梯比小颖走步行楼梯到达一层出口地面的时间快s．

查看试题解析
21. 盲盒顾名思义就是盒子中放置不同的物品，消费者凭运气抽中商品，正是这种随机化的体验，让消费者产生消费欲望，成为当下最热门的营销方法之一．某葡萄酒酒庄为回馈新老客户，也推出了盲盒式营销．商家计划在每件盲盒中放入 A，B 两种类型的酒，共 6 瓶．销售人员先包装了甲、乙两种盲盒．甲盲盒中装了 A 种酒 3 瓶，B 种酒 3 瓶；乙盲盒中装了 A 种酒 1 瓶，B 种酒 5 瓶；经过测算，甲盲盒的成本价为每件 240 元，乙盲盒的成本价为每件 160 元．

(1)、A 种酒和 B 种酒的成本价为每瓶多少元；

(2)、商家为回馈新老客户，计划所有的盲盒售价都为每件 299 元，请你再直接写出一种盲盒装箱的方案（题中两种方案除外），使它的成本价不高于 299 元．

查看试题解析
22. 请阅读下列材料，并完成相应的任务：
有趣的“飞镖图”
如图，这种形似飞镖的四边形，可以形象地称它为“飞镖图”．当我们仔细观察后发现，它实际上就是凹四边形．那么它具有哪些性质呢？又将怎样应用呢？下面我们进行认识与探究：凹四边形通俗地说，就是一个角“凹”进去的四边形，其性质有：凹四边形中最大内角外面的角等于其余三个内角之和．
（即如图 1，∠ADB=∠A＋∠B＋∠C ）理由如下：
方法一：如图 2，连接 AB，则在△ABC 中，∠C+∠CAB+∠CBA=180°，即∠1+∠2+∠3+∠4+∠C=180°，又∵在△ABD 中，∠1+∠2+∠ADB=180°，∴∠ADB=∠3+∠4+∠C，即∠ADB=∠CAD+∠CBD+∠C．
方法二：如图 3，连接 CD 并延长至 F，∵∠1 和∠3 分别是△ACD 和△BCD 的一个外角，. . . . . .
大家在探究的过程中，还发现有很多方法可以证明这一结论，你有自己的方法吗？
任务：

(1)、填空：“方法一”主要依据的一个数学定理是；

(2)、探索：根据“方法二”中辅助线的添加方式，写出该证明过程的剩余部分；

(3)、应用：如图 4，AE 是∠CAD 的平分线，BF 是∠CBD 的平分线，AE 与 BF 交于 G，若∠ADB=150°，∠AGB=110°，请你直接写出∠C 的大小．

查看试题解析
23. 如图，直线 y＝－x+4 和直线 y＝2x+1 相交于点 A，分别与 y 轴交于 B，C 两点．

(1)、求点 A 的坐标；

(2)、在 x 轴上有一动点 P（a，0），过点 P 作 x 轴的垂线，分别交函数 y＝－x+4和 y＝2x+1 的图象于点 D，E，若 DE＝6，求 a 的值．

(3)、在（2）的条件下，点 Q 为 x 轴负半轴上任意一点，直接写出△DEQ 为等腰三角形时 Q 点的坐标．

查看试题解析

	甲	乙	丙	丁
$\bar{x}$	90	103	95	108
S²	$\frac{26}{5}$	$\frac{18}{5}$	12	$\frac{18}{5}$

测试项目	创新能力	专业知识	语言表达
测试成绩/分	70	90	80