山西省晋城市阳城县2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-10-28 类型:期末考试
一、单选题
-
1. 下列各数中,是无理数的是( )A、 B、0 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 下列说法正确的是( )A、是无理数 B、7的平方根是 C、实数介于6和7之间 D、0.000000022可以用科学记数法表示为4. 等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )A、55°,55° B、70°,40°或70°,55° C、70°,40° D、55°,55°或70°,40°5. 下列命题的逆命题是真命题的是( )A、如果 , 那么, B、如果一个三角形有一个角是钝角,那么它的另外两个角是锐角 C、角平分线上的点到角两边的距离相等 D、如果一个整数的个位数字是5,那么这个整数能被5整除6. 课后延时服务已经落地,为了进一步对课后延时服务进行规范,某校计划在延时服务时间内开展各种社团活动.小明对全校学生进行抽样调查,收集整理拟参加社团活动类型(A.读书交流,B.体育锻炼,C.戏剧说唱,D.手工陶艺)数据后,绘制出两幅不完整的统计图,则下列说法错误的是( )
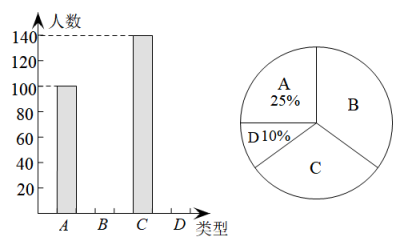 A、样本容量为400 B、类型D所对应的扇形的圆心角为36° C、类型C所占的百分比为 D、类型B的人数为120人7. 公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数 , 导致了第一次数学危机.是无理数的证明如下:
A、样本容量为400 B、类型D所对应的扇形的圆心角为36° C、类型C所占的百分比为 D、类型B的人数为120人7. 公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数 , 导致了第一次数学危机.是无理数的证明如下:假设是有理数,那么它可以表示成(p与q是互质的两个正整数).于是 , 所以, . 于是是偶数,进而q是偶数.从而可设 , 所以 , , 于是可得p也是偶数.这与“p与q是互质的两个正整数”矛盾,从而可知“是有理数”的假设不成立,所以是无理数.
这种证明“是无理数”的方法是( )
A、综合法 B、反证法 C、举反例法 D、数学归纳法8. 如图,在 中, ,以点 为圆心,适当长为半径画弧,分别交 于点 ,再分别以点 为圆心,大于 为半径画弧,两弧交于点 ,作射线 交边 于点 ,则 的面积是( ) A、 B、 C、 D、9. 七巧板是我们祖先的一项创造,它来源于勾股法,被誉为“东方魔板”,如图所示是一副七巧板,若已知等腰直角三角形的面积是1,则正方形的边长是( )
A、 B、 C、 D、9. 七巧板是我们祖先的一项创造,它来源于勾股法,被誉为“东方魔板”,如图所示是一副七巧板,若已知等腰直角三角形的面积是1,则正方形的边长是( )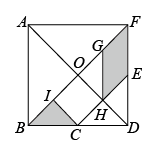 A、1 B、2 C、3 D、410. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( )
A、1 B、2 C、3 D、410. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( ) A、1,4,5 B、2,3,5 C、3,4,5 D、2,2,4
A、1,4,5 B、2,3,5 C、3,4,5 D、2,2,4二、填空题
-
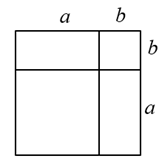
11. 若 ,则 .12. 若 , 直接写出; .13. 要表示一个家庭一年用于“教育”, “服装”,“食品”,“其他”这四项的支出各占家庭本年总支出的百分比,从“扇形统计图”,“条形统计图”,“折线统计图”中选择一种统计图,最适合的统计图是.14. 如图是一个重要公式的几何解释,请你写出这个公式 .
 15. 如图,中,边的垂直平分线交于点D,交于点E,连接 . 若 , 则的周长是 .
15. 如图,中,边的垂直平分线交于点D,交于点E,连接 . 若 , 则的周长是 .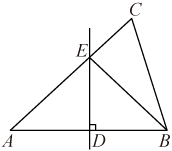 16. 为推动“双减”政策落实,切实解决学生负担,严格控制作业时间.政教处拟对全校560名学生每天做作业所用时间进行调查,调查人员随机抽取了部分学生进行问卷调查,并把结果制成如图所示的统计图,根据统计图可以估计这所学校学生“双减”政策落实后,每天做作业时间不少于1小时的人数为 .
16. 为推动“双减”政策落实,切实解决学生负担,严格控制作业时间.政教处拟对全校560名学生每天做作业所用时间进行调查,调查人员随机抽取了部分学生进行问卷调查,并把结果制成如图所示的统计图,根据统计图可以估计这所学校学生“双减”政策落实后,每天做作业时间不少于1小时的人数为 . 17. 如图,在中,是边上的中线,E是边上一点,过点C作交的延长线于点F,当 , , 时,的长是 .
17. 如图,在中,是边上的中线,E是边上一点,过点C作交的延长线于点F,当 , , 时,的长是 .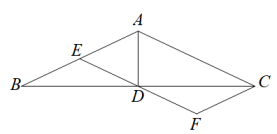 18. 如图,在边长为6的正方形 内作 , 交 于点 , 交 于点F,连接 ,将 绕点A顺时针旋转 得到 ,若 ,则 的长为.
18. 如图,在边长为6的正方形 内作 , 交 于点 , 交 于点F,连接 ,将 绕点A顺时针旋转 得到 ,若 ,则 的长为.
三、解答题
-
19.(1)、计算:(2)、先化简,再求值: , 其中 .20.(1)、计算: .(2)、计算:(3)、因式分解:(4)、因式分解:21. 一辆装满快递的物流卡车,其外形为高2.5米,宽1.6米的箱式货车,要开进厂门形状如图所示的工厂,问这辆车能否通过该工厂的厂门(厂门上方为半圆形拱门)?
 22. 如图,在和中, , , 点A,C,D依次在同一直线上,且 .
22. 如图,在和中, , , 点A,C,D依次在同一直线上,且 .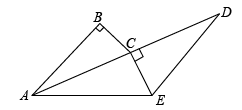 (1)、求证:;(2)、连接 , 当 , , 时,求的长.23. 为落实“双减”和“五项管理”,促进每一个孩子全面发展、健康成长,各级各部门都做出了有力举措.某班同学分三组进行教学实践活动调查,三组同学分别对七年级40名同学作业管理情况,八年级30名同学读物管理情况,九年级30名同学睡眠管理情况进行全面调查,并分别用扇形图、频数分布直方图、表格来描述得到的数据.
(1)、求证:;(2)、连接 , 当 , , 时,求的长.23. 为落实“双减”和“五项管理”,促进每一个孩子全面发展、健康成长,各级各部门都做出了有力举措.某班同学分三组进行教学实践活动调查,三组同学分别对七年级40名同学作业管理情况,八年级30名同学读物管理情况,九年级30名同学睡眠管理情况进行全面调查,并分别用扇形图、频数分布直方图、表格来描述得到的数据.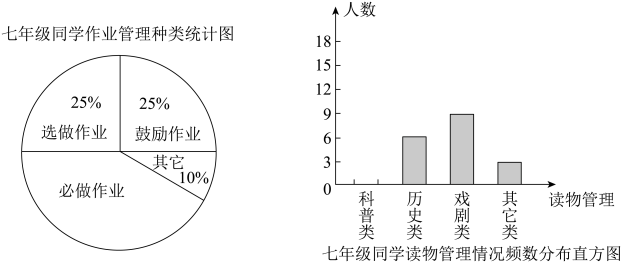
九年级同学睡眠管理时间情况统计表
时间
9小时左右
10小时左右
11小时左右
8小时左右
人数(人)
5
8
12
5
根据以上信息,请回答下列问题:
(1)、七年级40名同学中必做作业的人数是多少?(2)、补全八年级30名同学读物管理情况频数分布直方图:(3)、九年级30名同学睡眠时间的平均时间大约是多少小时?24. 已知中, , , (给出条件:① , ② . 在这2个条件中选择一个补充在前面的横线上),则的长是否存在?若存在,求出的长;若不存在,请说明理由. 25. 问题情境:已知,如下图,在梯形中,直线l,直线l,垂足分别为D,E,点C在直线l上, , .
25. 问题情境:已知,如下图,在梯形中,直线l,直线l,垂足分别为D,E,点C在直线l上, , .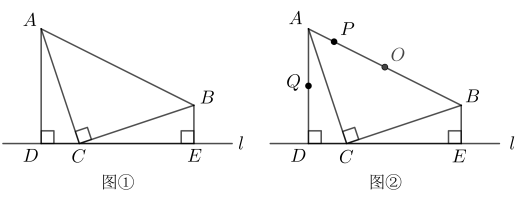 (1)、 猜想证明:
(1)、 猜想证明:如图①,试判断的形状,并说明理由;
(2)、 解决问题:如图①,若 , 求梯形的面积;
(3)、 拓展提升:如图②,设梯形的周长为m,边中点O处有两个动点P,Q同时出发,沿着的方向移动,点Q的速度是点P速度的3倍,当点P第一次到达点B时,两点同时停止移动.
①两点同时停止移动时,点Q移动的路程与点P移动的路程之差
 . (填“>”“<”或“=”)
. (填“>”“<”或“=”)②移动过程中点P能否和点Q相遇?如果能,则用直线a连接相遇点和点O,并探索直线a与的位置关系,写出推理过程:如不能,说明理由.