天津市西青区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列事件中，是随机事件的为（）

A、一个三角形的外角和是360° B、投掷一枚正六面体骰子，朝上一面的点数为5 C、在只装了红色卡片的袋子里，摸出一张白色卡片 D、明天太阳从西方升起

查看试题解析
2. 一个不透明的袋子中装有9个小球，其中6个红球，3个绿球，这些小球除颜色外无其他差别，从袋子中随机摸出一个小球，则摸出的小球是红球的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{9}$

查看试题解析
3. 下列图案中，可以看作是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列各数是方程x²＋3x－10＝0的根的是（）

A、2和5 B、－5和3 C、5和3 D、－5和2

查看试题解析
5. 如图，⊙O等边△ABC外接圆，点D是 $\overset{⌢}{B C}$ 上一点，连接AD，CD．若∠CAD＝25°，则∠ACD的度数为（）

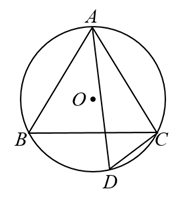A、85° B、90° C、95° D、100°

查看试题解析
6. 如图，OA是⊙O的半径，弦BC⊥OA，垂足为D．连接AC．若BC＝ $4 \sqrt{2}$ ， AC＝3，则⊙O的半径长为（）

A、9 B、8 C、 $\frac{9}{2}$ D、3

查看试题解析
7. 如图，已知点A，B，C是⊙O上三点，半径OC＝2，∠ABC＝30°，切线AP交OC延长线于点P，则AP长为（）

A、2 B、 $2 \sqrt{3}$ C、4 D、 $4 \sqrt{3}$

查看试题解析
8. 据某市交通部门统计，2018年底全市汽车拥有量为150万辆，而到2020年底，全市的汽车拥有量已达216万辆，求2018年底至2020年底该市汽车拥有量的年平均增长率，若设2018年底至2020年底该市汽车拥有量的年平均增长率为x，则可列方程为（）

A、 $150 (1 + 2 x) = 216$ B、 $150 \times 2 (1 + x) = 216$ C、 $150 (1 + x)^{2} = 216$ D、 $150 + 150 \times 2 x = 216$

查看试题解析
9. 如图，⊙O内切于△ABC，若∠AOC＝110°，则∠B的度数为（）

A、40° B、60° C、80° D、100°

查看试题解析
10. 如图， Rt△ABC的斜边AB＝13cm，一条直角边AC＝5cm，以BC边所在直线为轴将这个三角形旋转一周，得到一个圆锥，则这个圆锥的全面积为（）

A、65 $π$ cm² B、90 $π$ cm² C、156 $π$ cm² D、300 $π$ cm²

查看试题解析
11. 某种商品每件的进价为30元，在某时间段内若以每件x元出售，可卖出（100－x）件．若想获得最大利润，则定价x应为（）

A、35元 B、45元 C、55元 D、65元

查看试题解析
12. 已知抛物线y＝ax²＋bx＋c（a，b．c常数，a＜0）经过点（－1，0），其对称轴为直线x＝2，有下列结论：①c＜0；②4a＋b＝0；③4a＋c＞2b；④若y＞0，则－1＜x＜5；⑤关于x的方程ax²＋bx＋c＋1＝0有两个不等的实数根；⑥若 $M (3 ， y_{1})$ 与 $N (4 ， y_{2})$ 是此抛物线上两点，则 $y_{1} > y_{2}$ ．其中，正确结论的个数是（）

A、6 B、5 C、4 D、3

查看试题解析

二、填空题

13. 某瓷砖厂在相同条件下抽取部分瓷砖做耐磨实验，结果如下表所示：

抽取瓷砖数n	100	300	400	600	1000	2000	3000
合格品数m	96	282	382	570	949	1906	2850
合格品频率 $\frac{m}{n}$	0.960	0.940	0.955	0.950	0.949	0.953	0.950

则这个厂生产的瓷砖是合格品的概率估计值是．（精确到0.01）

查看试题解析

14. 若 $x_{1} ， x_{2}$ 是方程2x²＋4x－3＝0的两个根，则 $x_{1} \cdot x_{2}$ 的值为．

查看试题解析
15. 若二次函数y＝2x²－x＋k的图象与x轴有两个公共点，则k的取值范围是．

查看试题解析
16. 如图，六边形ABCDEF是半径为6的圆内接正六边形，则 $\overset{⌢}{C D}$ 的长为．

查看试题解析
17. 如图，已知△ABC内接于⊙O，BC是⊙O的直径，OD⊥AC于点D．半径OE⊥BC，连接BD，EA，且EA⊥BD点F．若BC＝10，则OD＝．

查看试题解析

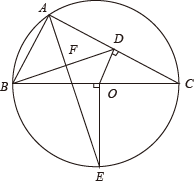
三、解答题

18. 如图，在每个小正方形的边长为1的网格中，△ABC的顶点A，C均在格点上，∠CAB＝26°，经过A，B，C三点的圆的半径为 $\sqrt{5}$ ．

(1)、线段AC的长等于；

(2)、请用无刻度的直尺，在如图所示的网格中，画出一个点M使其满足∠BMC＝38°，并简要说明点M的位置是如何找到的（不要求证明）．

查看试题解析
19. 解下列方程．

(1)、x（3x＋2）＝6（3x＋2）

(2)、3x²－2x－4＝0

查看试题解析
20. 在平面直角坐标系中，二次函数y＝－2x²＋bx＋c的图象经过点A（－2，4）和点B（1，－2）．

(1)、求这个二次函数的解析式及其图象的顶点坐标；

(2)、平移该二次函数的图象，使其顶点恰好落在原点的位置上，请直接说出平移的方向和距离．

查看试题解析
21. 如图，有一个可以自由转动的，分别标有－1，－2，3三个数字．小王和小李各转动一次转盘为一次游戏，当每次转盘停止后，指针所指扇形内的数为各自所得的数，一次游戏结束得到一组数（指针指在分界线时取指针右侧扇形的数）．

(1)、小王转动一次转盘指针指向正数所在扇形的概率是；

(2)、请你用树状图或列表的方法求一次游戏结束后两数之和是正数的概率．

查看试题解析
22. 已知AB是⊙O的直径，BD为⊙O的切线，切点为B．过⊙O上的点C作 $C D ∥ A B$ ，交BD点D．连接AC，BC．

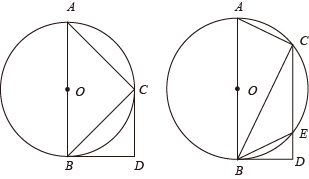(1)、如图①，若DC为⊙O的切线，切点为C．求∠BCD和∠DBC的大小；

(2)、如图②，当CD与⊙O交于点E时，连接BE．若∠EBD＝30°，求∠BCD和∠DBC的大小．

查看试题解析
23. 如图，若要建一个矩形场地，场地的一面靠墙，墙长10m，另三边用篱笆围成，篱笆总长20m，设垂直于墙的一边为xm，矩形场地的面积为Sm²

(1)、S与x的函数关系式为S＝，其中x的取值范围是；

(2)、若矩形场地的面积为42m² ，求矩形场地的长与宽．

(3)、当矩形场地的面积最大时，求矩形场地的长与宽，并求出矩形场地面积的最大值．

查看试题解析
24. 在等腰直角三角形ABC，∠BAC＝90°，AB＝AC．点D，E分别为AB，AC中点，F线段DE上一动点（不与点D，E重合），将线段AF绕点A逆时针方向旋转90°得到线段AG，连接GC，FB．

(1)、如图①，证明： $△ A F B ≅ △ A G C$ ．

(2)、如图②，连接GF，GE，GF交AE于点H．
①证明：在点F的运动过程中，总有∠FEG＝90°．
②若AB＝AC＝8，当DF的长度为多少时，△AHG等腰三角形？请直接写出DF的长度．

查看试题解析
25. 如图，在平面直角坐标系中，抛物线 $y = - \frac{1}{3} x^{2} + b x + 4$ 的对称轴是直线x＝2，与x轴相交于A，B两点（点A在点B的左侧），与y轴交于点C．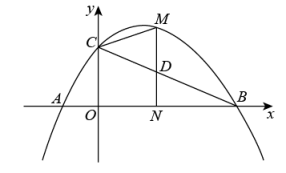

(1)、求b的值及B，C两点坐标；

(2)、M第一象限内抛物线上的一个点，过点M作MN⊥x轴于点N，交BC于点D．
①当线段MD的长取最大值时，求点M的坐标；
②连接CM，当线段 CM＝CD时，求点M坐标．

查看试题解析