天津市北辰区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 将抛物线 $y = 2 x^{2}$ 向上平移3个单位长度后得到新的抛物线，那么新抛物线的表达式为（）

A、 $y = 2 {(x - 3)}^{2}$ B、 $y = 2 {(x + 3)}^{2}$ C、 $y = 2 x^{2} - 3$ D、 $y = 2 x^{2} + 3$

查看试题解析
3. 下列事件为必然事件的是（）

A、口袋中装有2个红球和1个白球，从中摸出2个球，其中必有红球 B、明天会下雪 C、打开电视机，CCTV第一套节目正在播放新闻 D、购买一张彩票中奖一百万元

查看试题解析
4. 抛物线 $y = - 5 {(x - 1)}^{2} + 2$ 的顶点坐标为（）

A、 $(- 1, 2)$ B、 $(1, 2)$ C、 $(1, - 2)$ D、 $(2, 1)$

查看试题解析
5. 如图，A、B、C为 $⊙ O$ 上的三个点， $∠ A O B = 60 °$ ，则 $∠ C$ 的度数为（）

A、15° B、30° C、45° D、60°

查看试题解析
6. 如图，小球从A口往下落，在每个交叉口都有向左或向右两种可能，且可能性相同，则小球最终从E口落出的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{8}$

查看试题解析
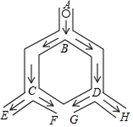7. 若关于x的一元二次方程 $k x^{2} + 2 x - 1 = 0$ 有两个不相等的实数根，则实数k的取值范围是（）

A、 $k > - 1$ B、 $k > - 1$ 且 $k \neq 0$ C、 $k < - 1$ D、 $k \geq - 1$ 且 $k \neq 0$

查看试题解析
8. 某校九年级组织一次篮球赛，各班均组队参赛，每两班之间都进行两场比赛，共需比赛12场，则九年级班级的个数为（）

A、6 B、5 C、4 D、3

查看试题解析
9. 如图，平面直角坐标系xOy中有4条曲线分别标注着①，②，③，④，是双曲线y＝﹣ $\frac{6}{x}$ 的一个分支的为（）

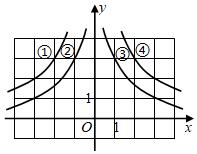A、① B、② C、③ D、④

查看试题解析
10. 关于反比例函数 $y = \frac{3}{x}$ 的图象性质，下列说法错误的是（）

A、图象经过点 $(1 ， 3)$ B、图象分别位于第一、三象限 C、图象关于原点对称 D、当 $x < 0$ 时，y随x的增大而增大

查看试题解析
11. 如图，将△ABC绕点A逆时针旋转65°得到△ADE，若∠E＝70°且AD⊥BC于点F，则∠BAC=（）

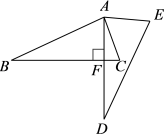A、80° B、85° C、90° D、95°

查看试题解析
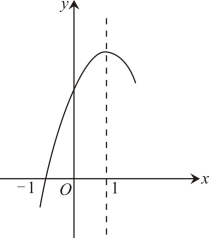12. 已知：抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的对称轴为直线 $x = 1$ ，与x轴的一个交点坐标为 $(- 1 ， 0)$ ，其部分图像如图所示，下列结论：① $a b c > 0$ ；② $b^{2} - 4 a c > 0$ ；③ $a - b + c = 0$ ；④方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的两个根是 $x_{1} = - 1$ ， $x_{2} = 3$ ；⑤ $8 a + c < 0$ ．其中正确的结论有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

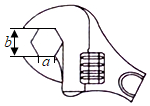
13. 已知关于x的一元二次方程 $x^{2} - 3 x + k - 2 = 0$ 的一个根是 $- 1$ ，则 $k =$ ．

查看试题解析
14. 一个不透明的口袋中装有7个红球，4个黄球，这些球除了颜色外无其它差别．从袋中随机摸取一个小球，它是红球的概率．

查看试题解析
15. 在函数 $y = \frac{2}{x}$ 的图象上有三点 $(- 3 ， y_{1})$ 、 $(- 2 ， y_{2})$ 、 $(1 ， y_{3})$ ，比较函数值 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小，并用“<”号连接．

查看试题解析
16. 如图，在拧开一个边长为a的正六角形螺帽时，扳手张开的开口 $b = 40 m m$ ，则边长a为mm．

查看试题解析
17. 某广场有一喷水池，水从地面喷出，如图，以水平地面为x轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线 $y = - x^{2} + 4 x$ （单位：米）的一部分，则水喷出的最大高度是米．

查看试题解析
18. 如图，C为线段AB的中点，D为AB垂直平分线上一点，连接BD，将BD绕点D顺时针旋转60°得到线段DE，连接AE，若 $A B = 2 \sqrt{3}$ ， $A E = 6$ ，则CD的长为．

查看试题解析

三、解答题

19. 如图，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图像经过点 $(- 2 ， 4)$ 和点 $A (a ， - 2)$ ．

(1)、求该反比例函数的解析式和a的值．

(2)、若点 $C (x ， y)$ 也在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图像上，当 $2 < x < 8$ 时，求函数y的取值范围．

查看试题解析
20. 已知如图，在 $⊙ O$ 中，AB为直径， $A B ⊥ C D$ ， $∠ A = 22.5 °$ ， $O D = 4$ ．

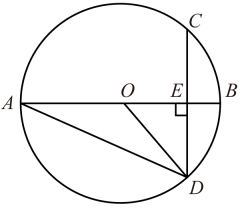(1)、求 $∠ O D C$ 的度数．

(2)、求CD的长．

查看试题解析
21. 用适当的方法解下列方程：

(1)、 $4 (x - 1)^{2} = 9$ ；

(2)、 $2 x^{2} - 3 x - 1 = 0$ ．

(3)、如图，在一块长13m，宽7m的矩形空地上，修建同样宽的两条互相垂直的道路（两条道路分别与矩形的一条边平行），剩余部分栽种花草，若栽种花草的面积是 $72 m^{2}$ ，则道路的宽应设计为多少m？

查看试题解析
22. 已知二次函数 $y = - x^{2} + 2 x + 3$

(1)、填写表中空格处的数值
x
…
$- 1$
1
2
…
$y = - x^{2} + 2 x + 3$
…
3
0
…

(2)、根据上表，画出这个二次函数的图象；

(3)、根据表格、图象，当 $0 < x < 4$ 时，y的取值范围．

查看试题解析
23. 四边形ABCD内接于 $⊙ O$ ， AC为其中一条对角线．

(1)、如图①，若 $∠ B A D = 70 °$ ， $B C = C D$ ，求 $∠ C A D$ 的度数；

(2)、如图②，若AD经过圆心O，CE为 $⊙ O$ 的切线，B为 $\overset{⌢}{A C}$ 的中点， $∠ D C E = 40 °$ ，求 $∠ B C E$ 的大小．

查看试题解析
24. 在平面直角坐标系中，已知点 $A (2 ， 0)$ ，点 $O (0 ， 0)$ ，点B在y轴正半轴上，且 $∠ B A O = 60 °$ ．

(1)、如图1， $△ A O B$ 绕着点O顺时针旋转，得 $△ A^{'} O B^{'}$ ，点A、B旋转后的对应点分别为 $A^{'}$ 、 $B^{'}$ ，记旋转角为 $α$ ． $A^{'} B^{'}$ 恰好经过点A时
①求此时旋转角 $α$ 的度数；
②求出此时点 $B^{'}$ 的坐标．

(2)、如图2，若 $0 ° < α < 90 °$ ，设直线 $A A^{'}$ 和直线 $B B^{'}$ 交于点P，猜测 $A A^{'}$ 与 $B B^{'}$ 的位置关系，并说明理由．

(3)、若 $0 ° < α < 360 °$ ，求（2）中的点P纵坐标的最小值（直接写出结果）．

查看试题解析
25. 已知抛物线 $y = a x^{2} + b x + 3 (a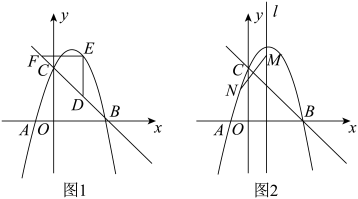 \neq 0)$ 交x轴交于 $A (- 1 ， 0)$ 和点 $B (3 ， 0)$ ，交y轴交于点C．

(1)、求抛物线的解析式；

(2)、如图1，点D是直线BC上一点，过点D作 $D E ∥ y$ 轴，交抛物线于点E（点E在点D的上方），再过点E作 $E F ∥ x$ 轴，交直线BC于点F．当 $△ D E F$ 的面积取最大值时，求点E的坐标；

(3)、如图2，点M为抛物线对称轴l上的一点，点N为抛物线上的一点，当直线BC垂直平分MN时，求出点N的坐标．

查看试题解析

x	…	$- 1$		1	2		…
$y = - x^{2} + 2 x + 3$	…		3			0	…