山西省长治市长子县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-10-28 类型:期末考试
一、单选题
-
1. 一元二次方程的解为( )A、x1=x2=2 B、x1=2,x2=﹣2 C、x1=x2=﹣2 D、x1=x2=42. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、3. 把抛物线向左平移2个单位,再向上平移3个单位,得到的抛物线是( )A、 B、 C、 D、4. 已知Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式中正确的是( )A、sinA= B、tanA= C、tanB= D、cosB=5. 小明在解方程x2﹣4x=2时出现了错误,解答过程如下:
∵a=1,b=﹣4,c=﹣2(第一步)
∴b2﹣4ac=(﹣4)2﹣4×1×(﹣2)=24(第二步)
∴(第三步)
∴(第四步)
小明解答过程开始出错的步骤是( )
A、第一步 B、第二步 C、第三步 D、第四步6. 甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( ) A、抛一枚硬币,连续两次出现正面的概率 B、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” C、任意写一个正整数,它能被5整除的概率 D、掷一枚正六面体的骰子,出现1点的概率7. 如图,小明探究课本“综合与实践”版块“制作视力表”的相关内容:当测试距离为时,标准视力表中最大的“
A、抛一枚硬币,连续两次出现正面的概率 B、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” C、任意写一个正整数,它能被5整除的概率 D、掷一枚正六面体的骰子,出现1点的概率7. 如图,小明探究课本“综合与实践”版块“制作视力表”的相关内容:当测试距离为时,标准视力表中最大的“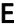 ”字高度为 , 当测试距离为时,最大的“
”字高度为 , 当测试距离为时,最大的“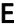 ”字高度为( )mm
”字高度为( )mm A、 B、 C、 D、8. 二次函数的图象如图所示,当-1<x<m时,y随x的增大而增大,则m的取值范围是( )
A、 B、 C、 D、8. 二次函数的图象如图所示,当-1<x<m时,y随x的增大而增大,则m的取值范围是( ) A、m>1 B、 C、m>0 D、-1<m<29. 如图1,是我们经常看到的一种折叠桌子,它是由下面的支架AD、BC与桌面构成,如图2,已知OA=OB=OC=OD=20cm,∠COD=60°,则点A到地面(CD所在的平面)的距离是( )
A、m>1 B、 C、m>0 D、-1<m<29. 如图1,是我们经常看到的一种折叠桌子,它是由下面的支架AD、BC与桌面构成,如图2,已知OA=OB=OC=OD=20cm,∠COD=60°,则点A到地面(CD所在的平面)的距离是( ) A、30cm B、60cm C、40cm D、60cm10. 如图,在平面直角坐标系中,正方形与正方形是以原点为位似中心的位似图形,且相似比为 , 点 , , 在轴上,若正方形的边长为6,则点坐标为( )
A、30cm B、60cm C、40cm D、60cm10. 如图,在平面直角坐标系中,正方形与正方形是以原点为位似中心的位似图形,且相似比为 , 点 , , 在轴上,若正方形的边长为6,则点坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 一元二次方程(2y﹣3)2=y(y+2)的一般形式是 .12. 小明同学在用描点法画二次函数y=a(x﹣h)2+k(a≠0)图像时,列出了下面表格:
x
……
﹣1
0
1
2
3
……
y
……
m
3
2
3
6
……
则m的值是 .
13. 如图,小明在某次投篮中刚好把球打到篮板的点D处后进球,已知小明与篮板底的距离BC=5米,眼睛与地面的距离AB=1.7米,视线AD与水平线的夹角为 ,已知 的值为0.3,则点D到地面的距离CD的长为米. 14. 如图,从一个大正方形中截去面积为和的两个小正方形,若随机向大正方形内投一粒米,则米粒落在图中阴影部分的概率为
14. 如图,从一个大正方形中截去面积为和的两个小正方形,若随机向大正方形内投一粒米,则米粒落在图中阴影部分的概率为 15. 如图,在 中, ,D是 上一点,且 ,连接 .若 ,则 的长为 .
15. 如图,在 中, ,D是 上一点,且 ,连接 .若 ,则 的长为 .
三、解答题
-
16. 计算: .17. 解方程:3x+6=(x+2)218. 在解决问题“已知 , 求的值”时,小明是这样分析与解答的:
,
,
请你根据小明的分析过程,解决如下问题:
若 , 求的值.
19. 张老师家的洗手盆上装有一种抬启式水龙头(如图①),完全开启后,把手 与水平线的夹角为 ,此时把手端点A、出水口点B和落水点C在同一直线上.洗手盆及水龙头示意图如图②,其相关数据为 , , , .求 的长(结果精确到 .参考数据: , , , ).
 20. 冰天雪地也是金山银山,北京张家口即将联合举办2022年北京冬季奥运会(简称“冬奥会“),在我国刮起了冰雪运动的旋风.某校为了了解七年级学生最喜爱的冬奥会项目,校团委宣传部李老师通过学校公众号向七年级学生发放调查问卷,要求如实填写并提交.
20. 冰天雪地也是金山银山,北京张家口即将联合举办2022年北京冬季奥运会(简称“冬奥会“),在我国刮起了冰雪运动的旋风.某校为了了解七年级学生最喜爱的冬奥会项目,校团委宣传部李老师通过学校公众号向七年级学生发放调查问卷,要求如实填写并提交.
收集数据:李老师从中随机抽查了40份问卷,得到如下数据:
ADABDCADEBEBCEDACADCCADDCDBDAECECDCADCDC
整理分析:李老师整理了这组数据并将结果绘制成两幅均不完整的统计图.

根据以上信息,回答下列问题:
(1)、请补全条形统计图.(2)、在扇形统计图中,m= , “项目E”所对应扇形圆心角的度数为 .(3)、最喜爱“B.滑冰”项目的有1名女生和3名男生,从中任选2名参加比赛,请用列表或画树状图的方法,求恰好选中1名男生和1名女生的概率.21. 某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示: (1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、该经销商想要每天获得150元的销售利润,销售价应定为多少?22. 问题情境:如图1,在△ABC中,AB=6,AC=5,点D,E分别在边AB,AC上,且 . 数学思考:
(1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、该经销商想要每天获得150元的销售利润,销售价应定为多少?22. 问题情境:如图1,在△ABC中,AB=6,AC=5,点D,E分别在边AB,AC上,且 . 数学思考: (1)、在图1中,的值为;(2)、图1中△ABC保持不动,将△ADE绕点A按逆时针方向旋转到图2的位置,其它条件不变,连接BD,CE,则(1)中的结论是否仍然成立?并说明理由;(3)、拓展探究:在图2中,延长BD,分别交AC,CE于点F,P,连接AP,得到图3,探究∠APE与∠ABC之间有何数量关系,并说明理由;(4)、若将△ADE绕点A按逆时针方向旋转到图4的位置,连接BD,CE,延长BD交CE的延长线于点P,BP交AC于点F,则(3)中的结论是否仍然成立,若成立,请说明理由;若不成立,请直接写出∠APE与∠ABC之间的数量关系.23. 在平面直角坐标系中,抛物线与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)、在图1中,的值为;(2)、图1中△ABC保持不动,将△ADE绕点A按逆时针方向旋转到图2的位置,其它条件不变,连接BD,CE,则(1)中的结论是否仍然成立?并说明理由;(3)、拓展探究:在图2中,延长BD,分别交AC,CE于点F,P,连接AP,得到图3,探究∠APE与∠ABC之间有何数量关系,并说明理由;(4)、若将△ADE绕点A按逆时针方向旋转到图4的位置,连接BD,CE,延长BD交CE的延长线于点P,BP交AC于点F,则(3)中的结论是否仍然成立,若成立,请说明理由;若不成立,请直接写出∠APE与∠ABC之间的数量关系.23. 在平面直角坐标系中,抛物线与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D. (1)、请直接写出点A,C,D的坐标;(2)、如图(1),在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;(3)、如图(2),点P为抛物线对称轴上的动点,使得△ACP为等腰三角形?若存在,求出点P的坐标,若不存在,请说明理由.
(1)、请直接写出点A,C,D的坐标;(2)、如图(1),在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;(3)、如图(2),点P为抛物线对称轴上的动点,使得△ACP为等腰三角形?若存在,求出点P的坐标,若不存在,请说明理由.