山西省阳泉市盂县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-28 类型：期末考试

进入出卷网下载

一、单选题

1. 抛物线y＝2（x﹣1）²﹣ $\frac{1}{2}$ 的顶点坐标为（）

A、（1，﹣ $\frac{1}{2}$ ） B、（﹣1，﹣ $\frac{1}{2}$ ） C、（﹣1， $\frac{1}{2}$ ） D、（1， $\frac{1}{2}$ ）

查看试题解析
2. 用配方法解方程x²﹣4x﹣5＝0时，原方程应变形为（　　）

A、（x﹣2）²＝9 B、（x﹣1）²＝6 C、（x+1）²＝6 D、（x+2）²＝6

查看试题解析
3. 如图所示，九（二）班的同学准备在坡角为α的河堤上栽树，要求相邻两棵树之间的水平距离为8 m，那么这两棵树在坡面上的距离AB为（）

A、8 $c o s α$ m B、 $\frac{8}{c o s α}$ m C、8sina m D、 $\frac{8}{s i n α}$ m

查看试题解析
4. 如图，C，D是⊙O上直径AB两侧的两点，设∠ABC＝35°，则∠BDC＝（　　）

A、85° B、75° C、70° D、55°

查看试题解析
5. 如图，在等边△ABC中，D是边AC上一点，连接BD．将△BCD绕点B逆时针旋转60°得到△BAE，连接ED．若BC = 6，BD =5，则△AED的周长是（）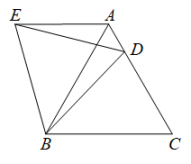

A、17 B、16 C、13 D、11

查看试题解析
6. 在一个不透明的袋中装有只有颜色不同的白球和红球共20个，某学习小组做摸球试验，将球搅匀后从中随机摸出一个球，记下颜色后再放回袋中；然后再重复上述步骤；…如表是实验中记录的部分统计数据：

摸球次数

40

50

60

80

100

200

摸到红球次数

19

10

13

16

20

40

则袋中的红球可能有（）

A、8个 B、6个 C、4个 D、2个

查看试题解析
7. 已知蓄电池的电压为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位： $Ω$ ）是反比例函数关系，它的图象如图所示．下列说法正确的是（）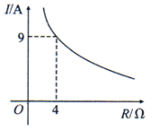

A、函数解析式为 $I = \frac{13}{R}$ B、蓄电池的电压是18V C、当 $I \leq 10 A$ 时， $R \geq 3.6 Ω$ D、当 $R = 6 Ω$ 时， $I = 4 A$

查看试题解析
8. 函数y＝kx﹣k与y $= \frac{- k}{x}$ 在同一平面直角坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
9. 如图， $△ A B C$ 中， $∠ A = 76 ° ， A B = 8 ， A C = 6$ ．将 $△ A B C$ 沿图示中的虚线剪开．剪下的阴影三角形与原三角形不相似的是（）

A、 B、 C、 D、

查看试题解析
10. 如图，已知抛物线y＝ax²+bx+c（a≠0）的对称轴为直线x＝1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，有下列结论：①4ac＜b²；②abc＞0；③方程ax²+bx+c＝0的两个根是x₁＝﹣1，x₂＝3；④当x＜0时，y随x增大而增大；⑤8a+c＜0其中结论正确的有（）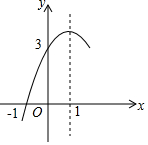

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 电影《长津湖》上映以来，全国票房连创佳绩．据不完全统计，某市第一天票房约2亿元，以后每天票房按相同的增长率增长，三天后累计票房收入达18亿元，将增长率记作x，则方程可以列为．

查看试题解析
12. 如果一个扇形的弧长等于它所在圆的半径，那么此扇形叫做“完美扇形”．已知某个“完美扇形”的周长等于6，那么这个扇形的面积等于．

查看试题解析
13. 一座石拱桥的桥拱是近似的抛物线形，建立如图所示的平面直角坐标系，其函数关系为 $y = - \frac{1}{16} x^{2}$ ，当水面的宽度AB为16米时，水面离桥拱顶的高度OC为m.

查看试题解析
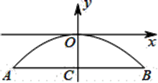14. 在等边△ABC中，P为BC上一点，D为AC上一点，且∠APD＝60°，BP＝4，CD＝2，则△ABC的边长为．

查看试题解析
15. 在平面直角坐标系中，直线 $l$ 经过点 $P (0 ， 3) ， Q (4 ， 0)$ ，若 $⊙ M$ 的半径为 $\frac{12}{5}$ ，圆心M在坐标轴上，且不与原点重合，当 $⊙ M$ 与直线 $l$ 相切时，则点M的坐标为.

查看试题解析

三、解答题

16. 计算：

(1)、计算：2cos60°+4sin60°•tan30°﹣6sin²45°；

(2)、解方程：x²﹣4＝3（x﹣2）．

查看试题解析
17. 如图所示的平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣3，2），B（﹣1，3），C（﹣1，1），请按如下要求画图：

(1)、以坐标原点O为旋转中心，将△ABC顺时针旋转90°，得到△A₁B₁C₁ ，请画出△A₁B₁C₁：并写出点B的对应点B₁的坐标；

(2)、以坐标原点O为位似中心，在x轴下方，画出△ABC的位似图形△A₂B₂C₂ ，使它与△ABC的位似比为2：1．并写出点B的对应点B₂的坐标．

(3)、△ABC内部一点M的坐标为（a，b），写出M在△A₂B₂C₂中的对应点M₂的坐标．

查看试题解析
18. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标，共享出行、共享服务、共享物品、共享知识，制成编号为A、B、C、D的四张卡片（除字母和内容外，其余完全相同）.现将这四张卡片背面朝上，洗匀放好.

(1)、小沈从中随机抽取一张卡片是“共享服务”的概率是；

(2)、小沈从中随机抽取一张卡片（不放回），再从余下的卡片中随机抽取一张，请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.（这四张卡片分别用它们的编号A、B、C、D表示）

查看试题解析
19. 如图，在平面直角坐标系中，一次函数y=2x+4的图象与x轴交于点A，与y轴交于点B，与反比例函数 $y = \frac{k}{x}$ （k≠0）的图象交于C，D两点，点C的坐标为（n，6）．

(1)、求该反比例函数的表达式；

(2)、求点D的坐标；

(3)、连接OC，OD，求 $△$ COD的面积．

查看试题解析
20. 如图，AB是⊙O的弦，C是⊙O外一点，OC⊥OA，OC交AB于点P，交⊙O于点D，且CP＝CB．

(1)、判断直线BC与⊙O的位置关系，并说明理由；

(2)、若∠A＝30°，OP＝ $\sqrt{3}$ ，求图中阴影部分的面积．

查看试题解析

21. 为了测量一条两岸平行的河流宽度，三个数学研究小组设计了不同的方案，他们在河南岸的点

A

处测得河北岸的树

H

恰好在

A

的正北方向.测量方案与数据如下表：

课题	测量河流宽度
测量工具	测量角度的仪器，皮尺等
测量小组	第一小组	第二小组	第三小组
测量方案示意图
说明	点 $B$ ， $C$ 在点 $A$ 的正东方向	点 $B$ ， $D$ 在点 $A$ 的正东方向	点 $B$ 在点 $A$ 的正东方向，点 $C$ 在点 $A$ 的正西方向
测量数据	$B C = 60 m$ ， $∠ A B H = 70 °$ ， $∠ A C H = 35 °$ .	$B D = 20 m$ ， $∠ A B H = 70 °$ ， $∠ B C D = 35 °$ .	$B C = 101 m$ ， $∠ A B H = 70 °$ ， $∠ A C H = 35 °$ .

(1)、哪个小组的数据无法计算出河宽？

(2)、请选择其中一个方案及其数据求出河宽（精确到

0.1 m

）；（参考数据：

s i n 70 ° \approx 0.94

，

s i n 35 ° \approx 0.57

，

t a n 70 ° \approx 2.75

，

t a n 35 ° \approx 0.70

）

(3)、计算的结果和实际河宽有误差，请提出一条减小误差的合理化建议.

查看试题解析

22. 如图，矩形ABCD中，∠ACB=30°，将一块直角三角板的直角顶点P放在两对角线AC，BD的交点处，以点P为旋转中心转动三角板，并保证三角板的两直角边分别于边AB，BC所在的直线相交，交点分别为E，F．

(1)、当PE⊥AB，PF⊥BC时，如图1，则 $\frac{PE}{PF}$ 的值为；

(2)、现将三角板绕点P逆时针旋转α（0°＜α＜60°）角，如图2，求 $\frac{PE}{PF}$ 的值；

(3)、在（2）的基础上继续旋转，当60°＜α＜90°，且使AP：PC=1：2时，如图3， $\frac{PE}{PF}$ 的值是否变化？证明你的结论．

查看试题解析
23. 如图①，已知抛物线 $y = a x^{2} + b x + 3$ （a≠0）与 $x$ 轴交于点A（1，0）和点B（－3，0），与y轴交于点C．

(1)、求抛物线的解析式；

(2)、设抛物线的对称轴与 $x$ 轴交于点M，问在对称轴上是否存在点P，使△CMP为等腰三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．

(3)、如图②，若点E为第二象限抛物线上一动点，连接BE、CE，求四边形BOCE面积的最大值，并求此时E点的坐标．

查看试题解析

摸球次数	40	50	60	80	100	200
摸到红球次数	19	10	13	16	20	40