山西省忻州市偏关县2019-2020学年九年级上学期期末考试数学试题
试卷更新日期:2022-10-28 类型:期末考试
一、单选题
-
1. 已知一次函数 , 从2,-3中随机取一个值,从1,-1,-2中随机取一个值,则该一次函数的图象经过第二、三、四象限的概率为( )A、 B、 C、 D、2. 若反比例函数y=﹣ 的图象经过点A(3,m),则m的值是( )
A、﹣3 B、3 C、﹣ D、3. 若是关于的方程的一个根,则此方程的另一个根( )A、-5 B、 C、5 D、4. 如图,是⊙的直径,为弦,且相交于点 , 则下列结论中不成立的是( )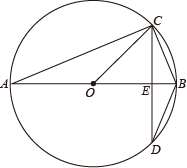 A、 B、 C、 D、5. 在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图象可能是( )A、
A、 B、 C、 D、5. 在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图象可能是( )A、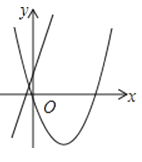 B、
B、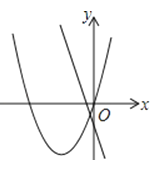 C、
C、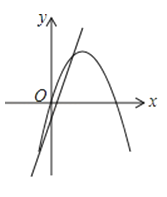 D、
D、 6. 如图,若将△ABC绕点C顺时针旋转90°后得到△A′B′C′,则A点的对应点A′的坐标是( )
6. 如图,若将△ABC绕点C顺时针旋转90°后得到△A′B′C′,则A点的对应点A′的坐标是( )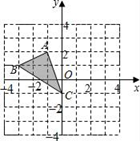 A、(﹣3,﹣2) B、(2,2) C、(3,0) D、(2,1)7. 物理某一实验的电路图如图所示,其中K1 , K2 , K3 为电路开关,L1 , L2为能正常发光的灯泡.任意闭合开关K1 , K2 , K3中的两个,那么能让两盏灯泡同时发光的概率为( )
A、(﹣3,﹣2) B、(2,2) C、(3,0) D、(2,1)7. 物理某一实验的电路图如图所示,其中K1 , K2 , K3 为电路开关,L1 , L2为能正常发光的灯泡.任意闭合开关K1 , K2 , K3中的两个,那么能让两盏灯泡同时发光的概率为( )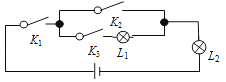 A、 B、 C、 D、8. 已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )
A、 B、 C、 D、8. 已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( ) A、abc<0 B、-3a+c<0 C、b2-4ac≥0 D、将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c9. 工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口的长度为( )
A、abc<0 B、-3a+c<0 C、b2-4ac≥0 D、将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c9. 工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口的长度为( )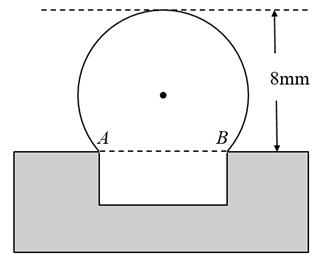 A、8mm B、6mm C、10mm D、0.9mm10. 学习了一次函数、二次函数、反比例函数后,爱钻研的小敏尝试用同样的方法研究函数y= , 从而得出以下命题:
A、8mm B、6mm C、10mm D、0.9mm10. 学习了一次函数、二次函数、反比例函数后,爱钻研的小敏尝试用同样的方法研究函数y= , 从而得出以下命题:⑴当x>0时,y的值随着x的增大而减小;
⑵y的值有可能等于3;
⑶当x>0时,y的值随着x的增大越来越接近3;
⑷当y>0时,x>0或x<- .
你认为真命题是 ( )
A、(1)(3) B、(1)(4) C、(1)(3)(4) D、(2)(3)(4)二、填空题
-
11. 已知 =6,则 的值是 .12. 已知正比例函数与反比例函数的一个交点是(2,3),则另一个交点是 .13. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为 .
 14. 如图所示,D是等腰内一点,BC是斜边,如果将绕点A逆时针方向旋转到的位置,则的度数为 .
14. 如图所示,D是等腰内一点,BC是斜边,如果将绕点A逆时针方向旋转到的位置,则的度数为 .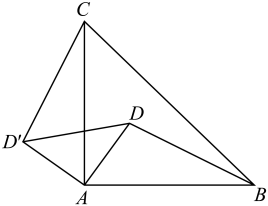 15. 如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0;②方程ax2+bx+c=0的根是x1=-1,x2=3;③a+b+c>0;④当x>1时,y随x的增大而增大.正确的有: .
15. 如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0;②方程ax2+bx+c=0的根是x1=-1,x2=3;③a+b+c>0;④当x>1时,y随x的增大而增大.正确的有: .
三、解答题
-
16. 解下列方程:(1)、(2)、17. 如图,桌面上放置了红,黄,蓝三个不同颜色的杯子,杯子口朝上,我们做蒙眼睛翻杯子(杯口朝上的翻为杯口朝下,杯口朝下的翻为杯口朝上)的游戏.
 (1)、随机翻一个杯子,求翻到黄色杯子的概率;(2)、随机翻一个杯子,接着从这三个杯子中再随机翻一个,请利用树状图求出此时恰好有一个杯口朝上的概率.18. 正方形绿化场地拟种植两种不同颜色(用阴影部分和非阴影部分表示)的花卉,要求种植的花卉能组成轴对称或中心对称图案,下面是三种不同设计方案中的一部分.
(1)、随机翻一个杯子,求翻到黄色杯子的概率;(2)、随机翻一个杯子,接着从这三个杯子中再随机翻一个,请利用树状图求出此时恰好有一个杯口朝上的概率.18. 正方形绿化场地拟种植两种不同颜色(用阴影部分和非阴影部分表示)的花卉,要求种植的花卉能组成轴对称或中心对称图案,下面是三种不同设计方案中的一部分.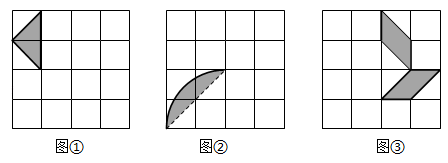
( 1 )请把图①、图②补成既是轴对称图形,又是中心对称图形,并画出一条对称轴;
( 2 )把图③补成只是中心对称图形,并把中心标上字母P.
19. 某商场销售一批名牌衬衫,平均每天售出20件,每件可盈利40元.为了扩大销售增加盈利,尽快减少库存,商场决定采取适当降价措施.调查发现,每件少盈利1元,商场平均每天可多售出2件衬衫.那么每件衬衫少盈利多少元时,商场平均每天盈利是1250元?20. 阅读材料并回答问题:(1)、方程的根为 , , , . 方程的根为 , , , . 程的根为 , , , .(2)、从(1)中你一定发现了一定的规律,这个规律是 .(3)、用你发现的规律解答下列问题:①不解方程,直接计算:方程的两根分别是、 , 则 ▲ , ▲ ;
②方程的两根分别是、 , 则 ▲ .
③已知一元二次方程的一个根为6,求及方程的另一个根.
21. 某汽车销售商推出分期付款购车促销活动,交首付款后,余额要在30个月内结清,不计算利息,王先生在活动期间购买了价格为12万元的汽车,交了首付款后平均每月付款 万元, 个月结清. 与 的函数关系如图所示,根据图像回答下列问题: (1)、确定 与 的函数解析式,并求出首付款的数目;(2)、王先生若用20个月结清,平均每月应付多少万元?(3)、如果打算每月付款不超过4000元,王先生至少要几个月才能结清余额?22. 如图所示,⊙的半径为1,直线CD经过圆心 , 交⊙于C、D两点,直径 , 点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙于点N,点P是直线CD上另一点,且 .
(1)、确定 与 的函数解析式,并求出首付款的数目;(2)、王先生若用20个月结清,平均每月应付多少万元?(3)、如果打算每月付款不超过4000元,王先生至少要几个月才能结清余额?22. 如图所示,⊙的半径为1,直线CD经过圆心 , 交⊙于C、D两点,直径 , 点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙于点N,点P是直线CD上另一点,且 .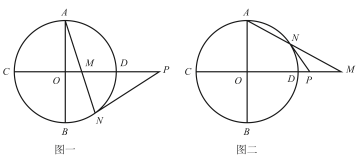 (1)、当点M在⊙内部,如图一,试判断PN与⊙的关系,并写出证明过程;(2)、当点M在⊙外部,如图二,其它条件不交时,(1)的结论是否还成立?请说明理由.23. 如图,在平面直角坐标系中,二次函数 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
(1)、当点M在⊙内部,如图一,试判断PN与⊙的关系,并写出证明过程;(2)、当点M在⊙外部,如图二,其它条件不交时,(1)的结论是否还成立?请说明理由.23. 如图,在平面直角坐标系中,二次函数 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.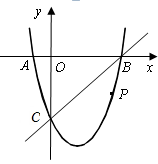 (1)、求二次函数解析式;(2)、连接PO,PC,并将△POC沿y轴对折,得到四边形 .是否存在点P,使四边形 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;(3)、当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
(1)、求二次函数解析式;(2)、连接PO,PC,并将△POC沿y轴对折,得到四边形 .是否存在点P,使四边形 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;(3)、当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.