山西省朔州市山阴县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-28 类型：期末考试

进入出卷网下载

一、单选题

1. 已知反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点 $A (2 ， 3)$ ，则下列的点在该反比例函数图象上的是（）

A、 $(- 1 ， 6)$ B、 $(- 3 ， 2)$ C、 $(- 3 ， - 2)$ D、 $(\frac{2}{3} ， - 9)$

查看试题解析
2. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 3$ ， $B C = 4$ ，则 $t a n A$ 的值是（）

A、 $\frac{3}{5}$ B、 $\frac{3}{4}$ C、 $\frac{5}{3}$ D、 $\frac{4}{3}$

查看试题解析
3. 用配方法解方程 $x^{2} - 6 x - 5 = 0$ 时，配方后的方程是（）

A、 $(x - 3)^{2} = 4$ B、 $(x - 3)^{2} = 14$ C、 $(x - 3)^{2} = 31$ D、 $(x + 3)^{2} = 14$

查看试题解析
4. 如图，直线 $a ， b ， c$ 截直线e和f， $a ∥ b ∥ c$ ， $\frac{A B}{B C} = \frac{2}{5}$ ，则下列结论中，正确的是（）

A、 $\frac{D F}{D E} = \frac{7}{2}$ B、 $\frac{E F}{D E} = \frac{3}{2}$ C、 $\frac{B E}{C F} = \frac{2}{5}$ D、 $\frac{D F}{E F} = \frac{5}{3}$

查看试题解析
5. 已知反比例函数 $y = - \frac{3}{x}$ ，则下列描述错误的是（）

A、图象位于第二、第四象限 B、图象必经过点 $(- 3 ， 1)$ C、图象不可能与坐标轴相交 D、y随x的增大而增大

查看试题解析
6. 据传说，古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理，在金字塔影子的顶部立一根木杆，借助太阳光线构成两个相似三角形，来测量金字塔的高度．已知木杆 $E F$ 长 $2 m$ ，它的影长 $F D$ 为 $3 m$ ，测得 $O A$ 为 $201 m$ ，则金字塔的高度 $B O$ 是（）

A、 $134 m$ B、 $152 m$ C、 $301.5 m$ D、 $315 m$

查看试题解析
7. 如图，某飞机于空中A处（探测的目标C的正上方），此时飞机的飞行高度 $A C = 1200 m$ ，从飞机上看地平面指挥台B的俯角 $∠ D A B = 30 °$ ．则飞机A与指挥台B的距离是（）

A、 $1200 \sqrt{2}$ 米 B、 $1200 \sqrt{3}$ 米 C、2400米 D、 $1200 \sqrt{5}$ 米

查看试题解析
8. 如图，在学习完概率后，同学们要确定如图1所示的图钉顶尖触地的概率．他们采用分组的方法，在相同的情况下，抛掷图钉，根据抛掷的次数和顶尖触地的频率绘制了图2的频率统计图，根据频率统计图可知，下列说法中，正确的是（）

A、由于图钉只能顶尖触地和顶尖朝上，因此抛掷一枚图钉时，顶尖朝上的概率是0.5 B、抛掷3次，一定有1次顶尖触地 C、抛掷一枚图钉，顶尖触地的概率是0.46 D、抛掷100次，顶尖触地的次数一定是46次

查看试题解析
9. 如图，在平面直角坐标系中， $△ A B C$ 与 $△ A^{'} B^{'} C^{'}$ 是位似图形，则位似中心是（）．

A、 $(6 ， 0)$ B、 $(7 ， 0)$ C、 $(6 ， 1)$ D、 $(7 ， 1)$

查看试题解析
10. 如图，已知菱形 $A B C D$ 的边长为8， $∠ A = 60 °$ ，点O是对角线 $B D$ 的中点．如图在点O处放置一个含 $60 °$ 角的三角板 $O M N$ ，把这个三角板绕点O旋转，斜边 $O N$ 与边 $A D$ 交于点F，直角边 $O M$ 与边 $D C$ 交于点E，若 $∠ M O N = 60 °$ ，则四边形 $O E D F$ 的面积是（）

A、随着三角板 $O M N$ 的位置的变化而变化 B、 $16 \sqrt{3}$ C、 $8 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析

二、填空题

11. 已知， $△ A B C$ 中， $∠ A$ 是锐角， $s i n A = \frac{1}{2}$ ，则 $∠ A$ 的度数是．

查看试题解析
12. 如图，A，B两点在反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象上， $A C ⊥ x$ 轴于点C， $B D ⊥ x$ 轴于点D，连接 $O B$ 交 $A C$ 于点E，若 $△ O A E$ 的面积是5，则四边形 $C D B E$ 的面积是．

查看试题解析
13. 一个不透明的袋中装有4个球，分别标有数字1，2，3，4，这些球除标有的数字不同外其余都完全相同．把袋中的球摇匀后，随机一次性摸出两个球，这两个球上的数字分别作为一个两位数的十位上的数字和个位上的数字，则这个两位数能被3整除的概率是．

查看试题解析
14. 如图， $△ A B O$ 中，以点O为圆心， $O A$ 为半径作 $⊙ O$ ，边 $A B$ 与 $⊙ O$ 相切于点A，把 $△ A B O$ 绕点A逆时针旋转得到 $△ A B^{'} O^{'}$ ，点O的对应点 $O^{'}$ 恰好落在 $⊙ O$ 上，则 $s i n ∠ B^{'} A B$ 的值是．

查看试题解析
15. 如图，正方形 $A B C D$ 的边长为 $12 c m$ ，点M和N在对角线 $B D$ 上，且 $B N = N M = M D$ ，连接 $A M$ 并延长交 $D C$ 于点E，连接 $E N$ 并延长交 $A B$ 于点F，则线段 $B F$ 的长为 $c m$ ．

查看试题解析

三、解答题

16. 解方程：

(1)、解方程： $(3 x - 2)^{2} = 4 x (3 x - 2)$ ；

(2)、计算： $s i n^{- 2} 30 ° - 2 c o s^{2} 45 ° + \sqrt{48} s i n 60 °$ ．

查看试题解析
17. 如图，利用标杆 $B E$ 测量建筑物 $C D$ 的高度．已知标杆 $B E$ 高 $1.2 m$ ，测得 $A B = 1.6 m$ ， $A C = 28 m$ ，点A，E，D在同一直线上，点B在 $A C$ 上．求该建筑物 $C D$ 的高度．

查看试题解析
18. 如图，有甲，乙两个转盘，甲转盘平均分成3等份，分别涂上红色、白色和蓝色，乙转盘平均分成两等份，分别涂上红色和白色，现在同时用力转动甲、乙两个转盘，两个指针只要有一个指针停在分界线上时，重新转动两个转盘，直到指针停在涂色的扇形区域．用列表或画树状图的方法，求两个指针都停在白色区域的概率．

查看试题解析
19. 某粮库需要把晾晒场上的1500吨玉米入库封存．

(1)、直接写出入库所需要的时间d（单位：天）与入库平均速度（单位：吨/天）的函数关系式（不必写出v的取值范围）；

(2)、已知粮库有职工50名，每天最多可入库300吨玉米．
①预计玉米入库最快可在几天内完成？
②粮库职工每天以最多的量把玉米入库，连续工作3天后，天气预报说未来几天会下雨，粮库决定次日把剩下的玉米全部入库，求至少需要增加多少职工？

查看试题解析
20. 如图，为了测量甲楼 $C D$ 的高度，由于甲楼的底部D不能直接到达，于是，测量人员在乙楼的顶部A测得甲楼的顶C的仰角是 $65 °$ ，底部D的俯角是 $45 °$ ，已知乙楼 $A B$ 的高度是12米，求甲楼 $C D$ 的高度．（参考数据： $s i n 65 ° \approx 0.91 ， c o s 65 ° \approx 0.42 ， t a n 65 ° \approx 2.14$ ，结果精确到0.1米）

查看试题解析
21. 某商店购进一种冬季取暖的“小太阳”取暖器，每台进价为40元．这种取暖器的销售价为每台52元时，每周可售出180台．经调查发现，销售定价每增加1元时，每周的销售量将减少10台，若商店准备把这种取暖器销售价定为每台x元 $(x \geq 52)$ ，每周的销售获利为y元．

(1)、求y与x的函数关系式（不必写出x的取值范围），并求出销售定价为多少时，这一周销售“小太阳”取暖器获利最大；

(2)、若该商店在某周销售这种“小太阳”取暖器获利2000元，求x的值．

查看试题解析
22. 综合与实践
问题情境：
在数学课上老师出了这样一道题：如图1，在 $△ A B C$ 中 $A B = A C = 6$ ， $∠ B A C = 30 °$ ，求 $B C$ 的长．

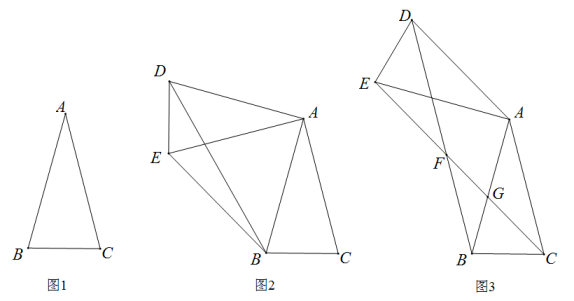(1)、探究发现：如图2，勤奋小组经过思考后，发现：把 $△ A B C$ 绕点A顺时针旋转 $90 °$ 得到 $△ A D E$ ，连接 $B D$ ， $B E$ ，利用直角三角形的性质即可求解，请你根据勤奋小组的思路，求 $B C$ 的长；

(2)、探究拓展：如图3，缜密小组的同学在勤奋小组的启发下，把 $△ A B C$ 绕点A顺时针旋转 $120 °$ 后得到 $△ A D E$ ，连接 $B D$ ， $C E$ 交于点F，交 $A B$ 于点G，请你判断四边形 $A D F C$ 的形状并证明；

(3)、奇异小组的同学把图3中的 $△ B G F$ 绕点B顺时针旋转，在旋转过程中，连接 $A F$ ，发现 $A F$ 的长度在不断变化，直接写出 $A F$ 的最大值和最小值．

查看试题解析
23. 综合与探究
如图，抛物线 $y = \frac{3}{4} x^{2} - \frac{15}{4} x + 3$ 与x轴交于A，B两点，且点A在点B的左侧，与y轴交于点C．

(1)、求点A，B和C的坐标；

(2)、点E是直线 $B C$ 上的动点，过点E作x轴的垂线交抛物线于点F，当 $E F = O C$ 时，求点E的横坐标；

(3)、点P从点B出发沿 $B C$ 以1个单位长度/秒的速度向终点C运动，同时，点Q从点O出发以相同的速度沿x轴的正半轴向终点B运动，一点到达，两点同时停止运动．连接 $P Q$ ，当 $△ B P Q$ 是等腰三角形时，请直接写出运动的时间．

查看试题解析