山西省吕梁市交口县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-10-28 类型:期末考试
一、单选题
-
1. 下列方程是一元二次方程的是( )A、3x2+y=2 B、x2﹣+1=0 C、x2﹣5x=3 D、x﹣3y+1=02. 如果关于x的方程 有实数根,那么m的取值范围是( )A、 B、 C、 D、3. 抛物线的顶点坐标是( )A、 B、 C、 D、4. 如图,将△ABC绕点C顺时针方向旋转40°得△A’CB’ , 若AC⊥A’B’ , 则∠BAC等于( )
 A、50° B、60° C、70° D、80°5. 利用配方法解一元二次方程时,将方程配方为(x-m)2=n,则、的值分别为( )A、 , B、 , C、 , D、 ,6. 第十四届全国运动会会徽吉祥物发布,吉祥物朱朱、熊熊、羚羚、金金的设计方案是以陕西秦岭独有的四种国宝级动物“朱鹮、大熊猫、羚牛、金丝猴”为创意原型.小明和小彬各从四个吉祥物中选择一个制作成绘画作品,参与学校举办的绘画展,则他们选中“朱朱”和“金金”的概率为( )
A、50° B、60° C、70° D、80°5. 利用配方法解一元二次方程时,将方程配方为(x-m)2=n,则、的值分别为( )A、 , B、 , C、 , D、 ,6. 第十四届全国运动会会徽吉祥物发布,吉祥物朱朱、熊熊、羚羚、金金的设计方案是以陕西秦岭独有的四种国宝级动物“朱鹮、大熊猫、羚牛、金丝猴”为创意原型.小明和小彬各从四个吉祥物中选择一个制作成绘画作品,参与学校举办的绘画展,则他们选中“朱朱”和“金金”的概率为( ) A、 B、 C、 D、7. 某建筑物,从10m高的窗口A , 用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面 m,则水流落地点B离墙的距离OB是( )
A、 B、 C、 D、7. 某建筑物,从10m高的窗口A , 用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面 m,则水流落地点B离墙的距离OB是( ) A、2m B、3m C、4m D、5m8. 如图,四边形ABCD内接于 , BC为直径,BD平分 , 若 , 则的度数为( )
A、2m B、3m C、4m D、5m8. 如图,四边形ABCD内接于 , BC为直径,BD平分 , 若 , 则的度数为( ) A、105° B、110° C、115° D、120°9. 在今年举办的东京奥运会上,杨倩在女子10米气步枪决赛中夺得冠军,为中国代表团揽入首枚金牌,随后杨倩同款“小黄鸭”发卡在电商平台上爆单,该款发卡在某电商平台上7月24日的销量为5000个,7月25日和7月26日的总销量是22500个.若月25日和26日较前一天的增长率均为x,则满足的方程是( )A、5000(1+x)2=22500 B、5000(1﹣x) 2=22500 C、5000+5000(1+x)+5000(1+x) 2=22500 D、5000(1+x)+5000(1+x) 2=2250010. 二次函数 的图象如图所示,对称轴是直线 .下列结论:① ;② ;③ ;④ ( 为实数).其中结论正确的个数为( )
A、105° B、110° C、115° D、120°9. 在今年举办的东京奥运会上,杨倩在女子10米气步枪决赛中夺得冠军,为中国代表团揽入首枚金牌,随后杨倩同款“小黄鸭”发卡在电商平台上爆单,该款发卡在某电商平台上7月24日的销量为5000个,7月25日和7月26日的总销量是22500个.若月25日和26日较前一天的增长率均为x,则满足的方程是( )A、5000(1+x)2=22500 B、5000(1﹣x) 2=22500 C、5000+5000(1+x)+5000(1+x) 2=22500 D、5000(1+x)+5000(1+x) 2=2250010. 二次函数 的图象如图所示,对称轴是直线 .下列结论:① ;② ;③ ;④ ( 为实数).其中结论正确的个数为( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 顶点是(1,3),开口方向、大小与 完全相同的抛物线解析式为;12. 如图, , 点O在边AB上,与边AC相切于点D,交边AB于点E,F,连接FD,则等于 .
 13. 袋中装有6个黑球和n个白球,经过若干次试验,发现“若从袋中任摸出一个球,恰是黑球的概率为 ,则这个袋中白球大约有个.14. 如图,在一块长15m、宽10m的矩形空地上,修建两条同样宽的相互垂直的道路,剩余分栽种花草,要使绿化面积为126m2 , 则修建的路宽应为米.
13. 袋中装有6个黑球和n个白球,经过若干次试验,发现“若从袋中任摸出一个球,恰是黑球的概率为 ,则这个袋中白球大约有个.14. 如图,在一块长15m、宽10m的矩形空地上,修建两条同样宽的相互垂直的道路,剩余分栽种花草,要使绿化面积为126m2 , 则修建的路宽应为米.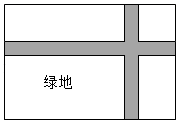 15. 已知二次函数与一次函数的图象相交于点和 , 如图所示,则使不等式成立的的取值范围是 .
15. 已知二次函数与一次函数的图象相交于点和 , 如图所示,则使不等式成立的的取值范围是 .
三、解答题
-
16. 解一元二次方程:(1)、;(用配方法)(2)、 .17. 某校为了解七、八年级学对生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理描述和分析部分信息如下:
a.七年级成线频数分布直方图:

b.七、八年级成绩的平均数、中位数如下:
年级
平均数
中位数
七
76.9
m
八
79.2
79.5
c.七年级成绩在这一组的是:70 72 74 75 76 76 77 77 77 78 79
根据以上信息,回答下列问题:
(1)、在这次测试中,七年级在80分以上(含80分)的有人,并写出表中m的值;(2)、在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两名学生在各自年级的排名谁更靠前,并说明理由;(3)、已知样本中成绩在50-60分的学生,其中有两名女生,若从这6人中随机选2人,求选到的两个人是一男一女的概率.18. 已知关于的方程 .(1)、求证:无论取何值,这个方程总有实数根;(2)、若等腰的一边长为6,且恰好是这个方程的一个根,求的周长.19. 如图,AB是⊙O的直径,点C是⊙O上一点,∠CAB的平分线AD交于点D,过点D作DE∥BC交AC的延长线于点E. (1)、求证:DE是⊙O的切线;(2)、若DE=2, CE=1,求BD的长度.20. 阅读下面材料:
(1)、求证:DE是⊙O的切线;(2)、若DE=2, CE=1,求BD的长度.20. 阅读下面材料:张明同学遇到这样一个问题:如图1,在正三角形ABC内有一点P,且 , , , 求的度数.
张明同学是这样思考的:如图2,利用旋转和全等的知识构造 , 连接 , 得到两个特殊的三角形,从而将问题解决.
 (1)、请你计算图1中的度数;(2)、参考张明同学思考问题的方法,解决下列问题:如图3,在正方形内有一点 , 且 , , , 求的度数.21. 今年是我国脱贫胜利年,我国在扶贫方面取得了巨大的成就,技术扶贫也使得我省某县的一个电子器件厂脱贫扭亏为盈.该电子器件厂生产一种电脑显卡,2019年该类电脑显卡的出厂价是200元/个,2020年,2021年连续两年在技术扶贫的帮助下改进技术,降低成本,2021年该电脑显卡的出厂价调整为162元/件.(1)、这两年此类电脑显卡出厂价下降的百分率相同,求平均每年下降的百分率.(2)、2021年某赛格电脑城以出厂价购进若干个此类电脑显卡,以200元/个销售时,平均每天可销售20个.为了减少库存,商场决定降价销售.经调查发现,单价每降低5元,每天可多售出10个,如果每天盈利1150元,单价应降低多少元?22. 综合与实践:如图1,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足 , 连接EF,求证: .
(1)、请你计算图1中的度数;(2)、参考张明同学思考问题的方法,解决下列问题:如图3,在正方形内有一点 , 且 , , , 求的度数.21. 今年是我国脱贫胜利年,我国在扶贫方面取得了巨大的成就,技术扶贫也使得我省某县的一个电子器件厂脱贫扭亏为盈.该电子器件厂生产一种电脑显卡,2019年该类电脑显卡的出厂价是200元/个,2020年,2021年连续两年在技术扶贫的帮助下改进技术,降低成本,2021年该电脑显卡的出厂价调整为162元/件.(1)、这两年此类电脑显卡出厂价下降的百分率相同,求平均每年下降的百分率.(2)、2021年某赛格电脑城以出厂价购进若干个此类电脑显卡,以200元/个销售时,平均每天可销售20个.为了减少库存,商场决定降价销售.经调查发现,单价每降低5元,每天可多售出10个,如果每天盈利1150元,单价应降低多少元?22. 综合与实践:如图1,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足 , 连接EF,求证: .
李伟同学是这样解决的:
将绕点A顺时针旋转90°得到 , 此时AB与AD重合,再证明 , 可得结论.
(1)、如图2,在四边形ABCD中, , , , 且 , , 求BE的长;(2)、类比(1)证明思想完成下列问题:在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点, , 若固定不动,绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),在旋转过程中,等式始终成立,请说明理由.23. 综合与探究:如图,在平面直角坐标系中,二次函数的图象经过点 , 点 .
 (1)、求此二次函数的解析式;(2)、当时,求二次函数的最大值和最小值;(3)、点P为此函数图象上任意一点,其横坐标为m,过点P作轴,点Q的横坐标为 . 已知点P与点Q不重合,且线段PQ的长度随m的增大而减小.求m的取值范围;
(1)、求此二次函数的解析式;(2)、当时,求二次函数的最大值和最小值;(3)、点P为此函数图象上任意一点,其横坐标为m,过点P作轴,点Q的横坐标为 . 已知点P与点Q不重合,且线段PQ的长度随m的增大而减小.求m的取值范围;