山西省吕梁市交城县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列交通标志中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若点A（-2，1）在反比例函数y= $\frac{k}{x}$ 的图象上，则k的值是（）

A、2 B、-2 C、 $\frac{1}{2}$ D、- $\frac{1}{2}$

查看试题解析
3. 已知2x=3y ，则下列比例式成立的是（）

A、 $\frac{x}{2} = \frac{3}{y}$ B、 $\frac{x + y}{y} = \frac{4}{3}$ C、 $\frac{x}{3} = \frac{y}{2}$ D、 $\frac{x + y}{x} = \frac{3}{5}$

查看试题解析
4. 如图，AD∥BE∥CF，AB=3，AC=9，DE=2，则EF的值为（）

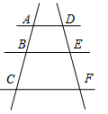A、2 B、3 C、4 D、5

查看试题解析
5. 在一个不透明的盒子中装有12个白球，若干个黄球，它们除颜色不同外，其余均相同．若从中随机摸出一个球是白球的概率是 $\frac{1}{3}$ ，则黄球的个数为（）

A、18 B、20 C、24 D、28

查看试题解析
6. 在反比例函数y= $\frac{k - 1}{x}$ 图像的每一支上，y都随x的增大而增大，则k的取值范围是（）

A、k>1 B、k>0 C、k≥1 D、k<1

查看试题解析
7. 如图，△ABC内接于⊙O ， AB为⊙O的直径，D为⊙O上一点（位于AB下方），CD交AB于点E ，若∠BDC＝45°，BC＝6 $\sqrt{2}$ ，CE＝2DE ，则CE的长为（）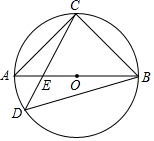

A、2 $\sqrt{6}$ B、4 $\sqrt{2}$ C、3 $\sqrt{5}$ D、4 $\sqrt{3}$

查看试题解析
8. 下列图形中，与如图所示的 $△$ ABC相似的是（）

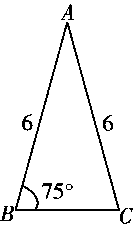A、 B、 C、 D、

查看试题解析
9. 对于二次函数y＝﹣（x﹣1）²+4，下列说法错误的是（）

A、当x＝1时，y有最大值3 B、当x≥1时，y随x的增大而减小 C、开口向下 D、函数图象与x轴交于点（﹣1，0）和（3，0）

查看试题解析
10. 一次函数 $y = a x + b$ 与二次函数 $y = a x^{2} + b x + c$ 在同一平面直角坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 若 $\frac{y}{x} = \frac{3}{4}$ ，则 $\frac{x + y}{x}$ 的值为.

查看试题解析
12. 如图，测量小玻璃管口径的量具ABC上，AB的长为10毫米，AC被分为60等份，如果小管口中DE正好对着量具上20份处（DE∥AB），那么小管口径DE的长是毫米．

查看试题解析
13. 如图，△A′B′C′是△ABC在点O为位似中心经过位似变换得到的，若△A′B′C′的面积与△ABC 的面积比是4：9，则OB′：OB为．

查看试题解析
14. 如图，矩形 $A B C D$ 的面积为4，顶点 $A$ 和 $D$ 在 $x$ 轴的正半轴上，顶点 $B ， C$ 分别落在反比例函数 $y_{1} = \frac{5}{x}$ 和 $y_{2} = \frac{k}{x}$ 的图象上，则 $k$ 的值等于．

查看试题解析
15. 如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，点D是AB的中点，以CD为直径作⊙O，⊙O分别与AC，BC交于点E，F，过点F作⊙O的切线FG，交AB于点G，则FG的长为．

查看试题解析

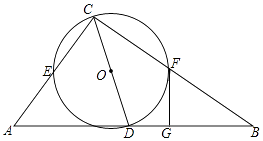
三、解答题

16. 用适当的方法解方程．

(1)、x²－6x＋2＝0；

(2)、(2x＋5)－3x(2x＋5)＝0．

查看试题解析
17. 如图，网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点，以格点为顶点，分别按下列要求画三角形．

(1)、在图②中，请在网格中画一个与图①△ABC相似的△DEF；

(2)、在图③中，以O为位似中心，画一个△A₁B₁C₁ ，使它与△ABC的位似比为2：1．

查看试题解析

18. “共和国勋章”获得者钟南山院士说：按照疫苗保护率达到70%计算，中国的新冠疫苗覆盖率需要达到近80%，才有可能形成群体免疫，本着自愿的原则，18至60周岁符合身体条件的中国公民均可免费接种新冠疫苗.居民甲、乙准备接种疫苗，其居住地及工作单位附近有两个大型医院和两个社区卫生服务中心均可免费接种疫苗，提供疫苗种类如下表：

接种地点		疫苗种类
医院	A	新冠病毒灭活疫苗
医院	B	重组新冠病毒疫苗（CHO细胞）
社区卫生服务中心	C	新冠病毒灭活疫苗
社区卫生服务中心	D	重组新冠病毒疫苗（CHO细胞）

若居民甲、乙均在A、B、C、D中随机独立选取一个接种点接种疫苗，且选择每个接种点的机会均等（提示：用A、B、C、D表示选取结果）

(1)、求居民甲接种的是新冠病毒灭活疫苗的概率；

(2)、请用列表或画树状图的方法求居民甲、乙接种的是相同种类疫苗的概率.

查看试题解析

19. 某网店正在热销一款电子产品，其成本为10元/件，销售中发现，该商品每天的销售量y（件）与销售单价x（元/件）之间存在如图所示的关系：

(1)、请求出y与x之间的函数关系式；

(2)、该款电子产品的销售单价为多少元时，每天销售利润最大？最大利润是多少元；

查看试题解析
20. 如图，在 $⊙ O$ 中，AB为 $⊙ O$ 的直径，直线DE与 $⊙ O$ 相切于点D ，割线 $A C ⊥ D E$ 于点E且交 $⊙ O$ 于点F ，连接DF ．

(1)、求证：AD平分∠BAC；

(2)、求证： $D F^{2} = E F \cdot A B$ ．

查看试题解析
21. 阅读理解：
从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．

(1)、如图1，在△ABC中，CD为∠ACB的角平分线，∠A＝40°，∠B＝60°，求证：CD为△ABC的完美分割线．

(2)、在△ABC中，∠A＝48°，CD为△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数．

查看试题解析
22. 综合与实践
背景阅读：旋转就是将图形上的每一点在平面内绕着旋转中心旋转固定角度的位置移动，其中“旋”是过程，“转”是结果．旋转作为图形变换的一种，具备图形旋转前后对应点到旋转中心的距离相等：对应点与旋转中心所连线段的夹角等于旋转角：旋转前、后的图形是全等图形等性质．所以充分运用这些性质是在解决有关旋转问题的关键．
实践操作：如图1，在Rt△ABC中，∠B＝90°，BC＝2AB＝12，点D，E分别是边BC，AC的中点，连接DE，将△EDC绕点C按顺时针方向旋转，记旋转角为α．

(1)、问题解决：①当α＝0°时， $\frac{A E}{B D}$ ＝；②当α＝180°时， $\frac{A E}{B D}$ ＝．

(2)、试判断：当0°≤a＜360°时， $\frac{A E}{B D}$ 的大小有无变化？请仅就图2的情形给出证明．

(3)、问题再探：当△EDC旋转至A，D，E三点共线时，求得线段BD的长为．

查看试题解析
23. 如图，直线 y=﹣x+2 与反比例函数 y= $\frac{k}{x}$ （k≠0）的图象交于 A（a，3）、B（3，b）两点，直线 AB 交 y 轴于点 C、交 x 轴于点 D．

(1)、请直接写出 a= ， b= ，反比例函数的解析式为．

(2)、在 x 轴上是否存在一点 E，使得∠EBD=∠OAC，若存在请求出点 E 的坐标，若不存在，请说明理由．

(3)、点P 是 x 轴上的动点，点 Q 是平面内的动点，是以 A、B、P、Q 为顶点的四边形是矩形，若存在请求出点 Q 的坐标，若不存在请说明理由．

查看试题解析