山西省临汾市尧都区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-28 类型：期末考试

进入出卷网下载

一、单选题

1. 已知⊙O的半径是5，点A到圆心O的距离是7，则点A与⊙O的位置关系是（）

A、点A在⊙O B、点A在⊙O内 C、点A在⊙O外 D、点A与圆心O重合

查看试题解析
2. 下列图形中，是轴对称图形，但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，在⊙O中， $\overset{⌢}{A B}$ 所对的圆周角∠ACB＝50°，若P为AB上一点，∠AOP＝55°，则∠POB的度数为（）

A、30° B、45° C、55° D、60°

查看试题解析
4. 抛物线y＝﹣2（x+1）²﹣3的对称轴是（）

A、直线x＝1 B、直线x＝﹣1 C、直线x＝3 D、直线x＝﹣3

查看试题解析
5. 已知点 $A (1, y_{1}), B (2, y_{2})$ 在抛物线 $y = - {(x + 1)}^{2} + 2$ 上，则下列结论正确的是（）

A、 $2 > y_{1} > y_{2}$ B、 $2 > y_{2} > y_{1}$ C、 $y_{1} > y_{2} > 2$ D、 $y_{2} > y_{1} > 2$

查看试题解析
6. 当 $b + c = 5$ 时，关于 $x$ 的一元二次方程 $3 x^{2} + b x - c = 0$ 的根的情况为（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
7. 把边长为3的正方形 $A B C D$ 绕点A顺时针旋转45°得到正方形 $A B^{'} C^{'} D^{'}$ ，边 $B C$ 与 $D^{'} C^{'}$ 交于点O，则四边形 $A B O D^{'}$ 的周长是（）

A、6 B、 $6 \sqrt{2}$ C、 $3 \sqrt{2}$ D、 $3 + 3 \sqrt{2}$

查看试题解析
8. 如图，二次函数 $y = a x^{2} + b x + c$ 的图象经过点 $A (1 ， 0)$ ， $B (5 ， 0)$ ，下列说法正确的是（）

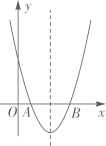A、 $c < 0$ B、 $b^{2} - 4 a c < 0$ C、 $a - b + c < 0$ D、图象的对称轴是直线 $x = 3$

查看试题解析
9. 从1、2、3、4四个数中随机选取两个不同的数，分别记为a、c ，则关于x的一元二次方程ax²＋4x＋c＝0有实数解的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
10. 如图，AC是矩形ABCD的对角线，⊙O是△ABC的内切圆，现将矩形ABCD按如图所示的方式折叠，使点D与点O重合，折痕为FG，点F，G分别在AD，BC上，连结OG，DG，若OG⊥DG，且⊙O的半径长为1，则下列结论不成立的是（）

A、CD+DF=4 B、CD−DF=2 $\sqrt{3}$ −3 C、BC+AB=2 $\sqrt{3}$ +4 D、BC−AB=2

查看试题解析

二、填空题

11. 一个正多边形的每个外角都等于 $60 °$ ，那么这个正多边形的中心角为.

查看试题解析
12. 一个小球在如图所示的方格地板上自由滚动，并随机停留在某块地板上，每块地板大小、质地完全相同，那么该小球停留在黑色区域的概率是.

查看试题解析
13. 二次函数y＝﹣（x﹣3）²+6的最大值是．

查看试题解析
14. 已知x₁ ， x₂是关于x的一元二次方程x²+2x+k﹣1＝0的两个实数根，且x₁²+x₂²﹣x₁x₂＝13，则k的值为.

查看试题解析
15. 点A的坐标为（－3，4），把点A绕着坐标原点逆时针旋转90°到点B，那么点B的坐标是.

查看试题解析
16. 如图，△DEC与△ABC关于点C成中心对称，AB＝3，AC＝1，∠D＝90°，则AE的长是．

查看试题解析
17. 五个完全相同的小长方形拼成如图所示的大长方形，大长方形的面积是135 $c m^{2}$ ，则以小长方形的宽为边长的正方形面积是 $c m^{2}$ .

查看试题解析
18. 如图，一个涵洞的截面边缘是抛物线形．现测得当水面宽AB＝1.6m时，涵洞顶点与水面的距离是2.4m．这时，离开水面1.5m处，涵洞的宽DE为．

查看试题解析

三、解答题

19. 解方程：x（x﹣2）+x﹣2＝0．

查看试题解析
20. 已知关于x的方程 $\frac{m - 1}{x - 1}$ － $\frac{x}{x - 1}$ ＝0无解，方程x²+kx+6＝0的一个根是m．

(1)、求m和k的值；

(2)、求方程x²+kx+6＝0的另一个根．

查看试题解析
21. 如图：△ABC绕点A逆时针方向旋转得到△ADE，其中∠B＝50°，∠C＝60°．

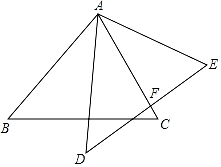(1)、若AD平分∠BAC时，求∠BAD的度数．

(2)、若AC⊥DE时，AC与DE交于点F，求旋转角的度数．

查看试题解析
22. 如图，已知O是坐标原点，B，C两点的坐标分别为（3，－1），（2，1），将 $△$ BOC绕点O逆时针旋转90度，得到 $△$ B₁OC₁ ．请画出 $△$ B₁OC₁ ，并写出B，C两点的对应点B₁ ， C₁的坐标．

查看试题解析
23. 图1是一枚质地均匀的正四面体形状的骰子，每个面上分别标有数字2，3，4，5.图2是一个正六边形棋盘，现通过掷骰子的方式玩跳棋游戏，规则是：将这枚骰子在桌面掷出后，看骰子落在桌面上（即底面）的数字是几，就从图中的 $A$ 点开始沿着顺时针方向连续跳动几个顶点，第二次从第一次的终点处开始，按第一次的方法继续……

(1)、随机掷一次骰子，则棋子跳动到点 $C$ 处的概率是.

(2)、随机掷两次骰子，用画树状图或列表的方法，求棋子最终跳动到点 $C$ 处的概率.

查看试题解析
24. 某养殖场为了响应党中央的扶贫政策，今年起采用“场内+农户”养殖模式，同时加强对蛋鸡的科学管理，蛋鸡的产蛋率不断提高，三月份和五月份的产蛋量分别是2.5万kg与3.6万kg，现假定该养殖场蛋鸡产蛋量的月增长率相同.

(1)、求该养殖场蛋鸡产蛋量的月平均增长率；

(2)、假定当月产的鸡蛋当月在各销售点全部销售出去，且每个销售点每月平均销售量最多为0.32万kg.如果要完成六月份的鸡蛋销售任务，那么该养殖场在五月份已有的销售点的基础上至少再增加多少个销售点？

查看试题解析
25. 如图，以△ABC的边AB为直径画⊙O，交AC于点D，半径OE//BD，连接BE，DE，BD，设BE交AC于点F，若∠DEB=∠DBC．

(1)、求证：BC是⊙O的切线；

(2)、若BF=BC=2，求图中阴影部分的面积．

查看试题解析
26. 如图1，抛物线 $y = a x^{2} + b x + 6$ 与x轴交于点 $A (- 2 ， 0)$ ， $B (6 ， 0)$ ，与y轴交于点C，顶点为D，直线AD交y轴于点E．

(1)、求抛物线的解析式．

(2)、如图2，将 $△ A O E$ 沿直线AD平移得到 $△ N M P$ ．
①当点M落在抛物线上时，求点M的坐标．
②在 $△ N M P$ 移动过程中，存在点M使 $△ M B D$ 为直角三角形，请直接写出所有符合条件的点M的坐标．

查看试题解析