山西省临汾市襄汾县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-28 类型：期末考试

进入出卷网下载

一、单选题

1. 计算 ${(\sqrt{3})}^{2}$ 的结果是（）

A、 $\sqrt{3}$ B、3 C、 $2 \sqrt{3}$ D、9

查看试题解析
2. 某校有4000名学生，随机抽取了400名学生进行体重调查，下列说法错误的是（）

A、总体是该校4000名学生的体重 B、个体是每一个学生 C、样本是抽取的400名学生的体重 D、样本容量是400

查看试题解析
3. 用配方法解方程 $x^{2} - 6 x + 5 = 0$ ，配方后所得的方程是（）

A、 ${(x + 3)}^{2} = - 4$ B、 ${(x - 3)}^{2} = - 4$ C、 ${(x + 3)}^{2} = 4$ D、 ${(x - 3)}^{2} = 4$

查看试题解析
4. 如图，△ABC与△DEF位似，点O是它们的位似中心，其中OE=2OB，则△ABC与△DEF的周长之比是（）

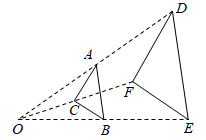A、1：2 B、1：4 C、1：3 D、1：9

查看试题解析
5. 如图是一架人字梯，已知 $A B = A C = 2$ 米，AC与地面BC的夹角为 $α$ ，则两梯脚之间的距离BC为（）

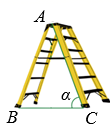A、 $4 \cos α$ 米 B、 $4 \sin α$ 米 C、 $4 \tan α$ 米 D、 $\frac{4}{\cos α}$ 米

查看试题解析
6. 一只不透明的袋子中装有3个黑球和2个白球，这些除颜色外无其他差别，从中任意摸出3个球，下列事件是确定事件的为（）

A、至少有1个球是黑球 B、至少有1个球是白球 C、至少有2个球是黑球 D、至少有2个球是白球

查看试题解析
7. 如图，已知点O是△ABC的外心，∠A=40°，连结BO，CO，则∠BOC的度数是（）

A、60° B、70° C、80° D、90°

查看试题解析
8. 学校招募运动会广播员，从两名男生和两名女生共四名候选人中随机选取两人，则两人恰好是一男一女的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
9.
如图，一根5m长的绳子，一端拴在围墙墙角的柱子上，另一端拴着一只小羊A(羊只能在草地上活动)，那么小羊A在草地上的最大活动区域面积是（）

A、 $\frac{17}{12}$ πm² B、 $\frac{17}{6}$ πm² C、 $\frac{25}{4}$ πm² D、 $\frac{77}{12}$ πm²

查看试题解析
10. 抛物线的函数表达式为 $y = 3 {(x - 2)}^{2} + 1$ ，若将 $x$ 轴向上平移2个单位长度，将 $y$ 轴向左平移3个单位长度，则该抛物线在新的平面直角坐标系中的函数表达式为（）

A、 $y = 3 {(x + 1)}^{2} + 3$ B、 $y = 3 {(x - 5)}^{2} + 3$ C、 $y = 3 {(x - 5)}^{2} - 1$ D、 $y = 3 {(x + 1)}^{2} - 1$

查看试题解析

二、填空题

11. 使 $\sqrt{\frac{2}{x}}$ 有意义的x的取值范围是 .

查看试题解析
12. 关于x的方程 $x^{2} - 4 x + m = 0$ 有两个不相等的实数根，则m的取值范围是．

查看试题解析
13. 图1是装了液体的高脚杯示意图（数据如图），用去一部分液体后如图2所示，此时液面 $A B =$ .

查看试题解析
14. 如图，是一个横断面为抛物线形状的拱桥，当水面宽4m时，拱顶（拱桥洞的最高点）离水面2m，当水面上升1m时，水面的宽为．

查看试题解析
15. 如图，在边长为2的正方形 $A B C D$ 中， $A E$ 是以 $B C$ 为直径的半圆的切线，则图中阴影部分的面积为.

查看试题解析

三、解答题

16. 计算

(1)、 ${(- 1)}^{2021} + \sqrt{8} - 4 s i n 45 ° + | - 2 |$

(2)、 $| - \sqrt{2} | + {(\sqrt{2} - \frac{1}{2})}^{2} - {(\sqrt{2} + \frac{1}{2})}^{2}$

查看试题解析

17. 小敏与小霞两位同学解方程

3 (x - 3) = {(x - 3)}^{2}

的过程如下框：

小敏：

两边同除以 $(x - 3)$ ，得

$3 = x - 3$ ，

则 $x = 6$ ．

小霞：

移项，得 $3 (x - 3) - {(x - 3)}^{2} = 0$ ，

提取公因式，得 $(x - 3) (3 - x - 3) = 0$ ．

则 $x - 3 = 0$ 或 $3 - x - 3 = 0$ ，

解得 $x_{1} = 3$ ， $x_{2} = 0$ ．

你认为他们的解法是否正确？若正确请在框内打“√”；若错误请在框内打“×”，并写出你的解答过程．

查看试题解析

18. 如图，AB是 $⊙ O$ 的直径，点F在 $⊙ O$ 上，∠BAF的平分线AE交 $⊙ O$ 于点E，过点E作 $E D ⊥ A F$ ，交AF的延长线于点D，延长DE、AB相交于点C．求证：CD是 $⊙ O$ 的切线；

查看试题解析
19. “杂交水稻之父”——袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量700公斤的目标，第三阶段实现水稻亩产量1008公斤的目标．

(1)、如果第二阶段、第三阶段亩产量的增长率相同，求亩产量的平均增长率；

(2)、按照（1）中亩产量增长率，科研团队期望第四阶段水稻亩产量达到1200公斤，请通过计算说明他们的目标能否实现．

查看试题解析
20. 越来越多太阳能路灯的使用，既点亮了城市的风景，也是我市积极落实节能环保的举措.某校学生开展综合实践活动，测量太阳能路灯电池板离地面的高度.如图，已知测倾器的高度为1.6米，在测点A处安置测倾器，测得点M的仰角 $∠ M B C = 33 °$ ，在与点A相距3.5米的测点D处安置测倾器，测得点M的仰角 $∠ M E C = 45 °$ （点A，D与N在一条直线上），求电池板离地面的高度 $M N$ 的长.（结果精确到1米；参考数据： $\sin 33 ° \approx 0.54 ， \cos 33 ° \approx 0.84 ， \tan 33 ° \approx 0.65$ ）

查看试题解析
21. 目前，全国各地正在有序推进新冠疫苗接种工作．某单位为了解职工对疫苗接种的关注度，随机抽取了部分职工进行问卷调查，调查结果分为：A（实时关注）、B（关注较多）、C（关注较少）、D（不关注）四类，现将调查结果绘制成如图所示的统计图．

请根据图中信息，解答下列问题：

(1)、求C类职工所对应扇形的圆心角度数，并补全条形统计图；

(2)、若D类职工中有3名女士和2名男士，现从中任意抽取2人进行随访，请用树状图或列表法求出恰好抽到一名女士和一名男士的概率．

查看试题解析
22.

(1)、【证明体验】
如图1， $A D$ 为 $△ A B C$ 的角平分线， $∠ A D C = 60 °$ ，点E在 $A B$ 上， $A E = A C$ ．求证： $D E$ 平分 $∠ A D B$ ．

(2)、【思考探究】
如图2，在（1）的条件下，F为 $A B$ 上一点，连结 $F C$ 交 $A D$ 于点G．若 $F B = F C$ ， $D G = 2$ ， $C D = 3$ ，求 $B D$ 的长．

(3)、【拓展延伸】
如图3，在四边形 $A B C D$ 中，对角线 $A C$ 平分 $∠ B A D ， ∠ B C A = 2 ∠ D C A$ ，点E在 $A C$ 上， $∠ E D C = ∠ A B C$ ．若 $B C = 5 ， C D = 2 \sqrt{5} ， A D = 2 A E$ ，求 $A C$ 的长．

查看试题解析
23. 如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与x轴交于A、B两点，与y轴交于C点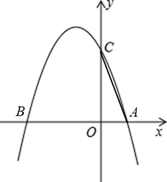， $A C = \sqrt{10}$ ， $O B = O C = 3 O A$ .

(1)、求抛物线的解析式；

(2)、在第二象限内的抛物线上确定一点P，使四边形PBAC的面积最大.求出点P的坐标

(3)、在（2）的结论下，点M为x轴上一动点，抛物线上是否存在一点Q.使点P、B、M、Q为顶点的四边形是平行四边形，若存在.请直接写出Q点的坐标；若不存在，请说明理由.

查看试题解析