山西省临汾市洪洞县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-10-28 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，已知点A的坐标是 $(5 ， 3)$ ，则点A关于原点对称的点 $A^{'}$ 的坐标是（）

A、 $(- 3 ， 5)$ B、 $(3 ， - 5)$ C、 $(- 3 ， - 5)$ D、 $(- 5 ， - 3)$

查看试题解析
2. 下列运算中，正确的是（）

A、 $\sqrt{3} + \sqrt{13} = 4$ B、 $\sqrt{7} - \sqrt{2} = \sqrt{5}$ C、 $\sqrt{5} \times \sqrt{15} = 5 \sqrt{3}$ D、 $(\sqrt{12} + \sqrt{27}) \div \sqrt{3} = 7$

查看试题解析
3. 如图，在△ABC中， $∠ A C B = 90 °$ ， $A C = 12$ ， $B C = 5$ ，则下列说法正确的是（）

A、 $s i n A = \frac{5}{12}$ B、 $c o s A = \frac{12}{13}$ C、 $s i n B = \frac{5}{13}$ D、 $t a n B = \frac{5}{12}$

查看试题解析
4. 下列事件是必然事件的是（）

A、打开电视机，它正在播广告 B、篮球队员在罚球线上投篮一次，投中 C、经过有信号灯的路口，遇到绿灯 D、投掷一枚质地均匀的普通正方体骰子，掷得的数不是奇数就是偶数

查看试题解析
5. 方程 $3 x^{2} - 2 x - 5 = 0$ 的根的情况，下列说法正确的是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
6. 已知二次函数 $y = 2 x^{2} + 3$ 的图象沿x轴向右平移1个单位长度，沿y轴向下平移5个单位长度，则平移后的图象的解析式是（）

A、 $y = 2 {(x + 1)}^{2} - 2$ B、 $y = 2 {(x - 1)}^{2} - 2$ C、 $y = 2 {(x - 5)}^{2} + 2$ D、 $y = 2 {(x + 5)}^{2} + 4$

查看试题解析
7. 如图，在 $5 \times 4$ 的小正方形网格中，点A，B，C都在格点上（格点是指网格中小正方形的顶点），则 $t a n ∠ A B C$ 的值是（）

A、 $\frac{4}{5}$ B、 $\frac{1}{2}$ C、 $\frac{2}{5}$ D、 $\frac{1}{3}$

查看试题解析
8. 为了估计河的宽度，在河的对岸选定一个目标作为点A．再在河的这一边选定点B和C，使 $A B ⊥ B C$ ，然后再选定点E，使 $E C ⊥ B C$ ，用视线确定BC与AE交于点D．此时，测得 $B D = 120 m$ ， $D C = 60 m$ ， $E C = 50 m$ ，则两岸间的距离AB是（）

A、120m B、110m C、100m D、90m

查看试题解析
9. 小明与父母周末在公园放风筝．小明放一个线长为150米的风筝，他的风筝线（近似地看作直线）与水平地面构成60°的角．若小明的身高1.2米，则他的风筝的高度是（）

A、76.2米 B、 $(1.2 + 50 \sqrt{3})$ 米 C、 $(1.2 + 75 \sqrt{2})$ 米 D、 $(1.2 + 75 \sqrt{3})$ 米

查看试题解析
10. 如图是抛物线 $y = a x^{2} + b x + c$ 的部分图象，该图象的对称轴是直线 $x = - \frac{1}{2}$ ，与x轴的一个交点A的坐标是（−3，0），则关于x的一元二次方程 $a x^{2} + b x + c = 0$ 的解是（）

A、 $x_{1} = - 3$ ， $x_{2} = 2$ B、 $x_{1} = 3$ ， $x_{2} = - 2$ C、 $x_{1} = - 3$ ， $x_{2} = 3$ D、 $x_{1} = - 3$ ， $x_{2} = - \frac{1}{2}$

查看试题解析

二、填空题

11. 计算： $(\sqrt{13} + \sqrt{2}) (\sqrt{13} - \sqrt{2})$ 的结果是．

查看试题解析
12. 一个三角形的三边长分别为 6，8，10，则这个三角形最长边上的中线为．

查看试题解析
13. 如图，在学习完概率后，同学们要确定如图1所示的图钉的顶尖触地的概率．他们采用分组的方法，在相同的情况下，抛掷图钉，根据抛掷的次数和顶尖触地的频率绘制了图2的频率统计图，根据频率统计图可知，顶尖触地的概率是．

查看试题解析
14. 在“双减”政策下，学校开展了丰富多彩的活动，其中，要举办一次摄影展览，在每张长和宽分别为20cm和15cm的矩形相片周围镶上一圈等宽的彩纸．经试验，彩纸面积为相片面积的 $\frac{1}{3}$ 时较美观．若所镶彩纸的宽为xcm，根据题意，列方程为．

查看试题解析
15. 如图，在▱ABCD中， $A B = 8$ ， $B C = 12$ ，把▱ABCD绕点A逆时针旋转得到 $▱ A B^{'} C^{'} D^{'}$ ．点 $B^{'}$ 落在BC边上， $B B^{'} = 4$ ， $B^{^{'}} C^{^{'}}$ 交CD边于点E， $C^{^{'}} D^{^{'}}$ 边经过点D，则CE的长是．

查看试题解析

三、解答题

16.

(1)、 $\sqrt{48} + \sqrt{12} c o s 30 ° - \frac{s i n 60 °}{s i n 30 °}$ ；

(2)、下面是小明同学解一元二次方程的过程，请仔细阅读，并完成相应的任务．
解方程： ${(3 x - 1)}^{2} = 2 (3 x - 1)$ ．
解：方程两边同除以 $(3 x - 1)$ ，得    $3 x - 1 = 2$ ． ……第一步
移项，合并同类项，得    $3 x = 3$ ． ……第二步
系数化为1，得 $x = 1$ ． ……第三步
任务：
①小明的解法从第  ▲  步开始出现错误；
②此题的正确结果是  ▲   ．
③用因式分解法解方程： $3 x (x + 2) = 2 x + 4$ ．

查看试题解析
17. 如图，在平面直角坐标系中，△ABC的三个顶点的坐标都是整数，点A的坐标为 $(2 ， 1)$ ，点P的坐标为 $(0 ， 1)$ ．请解答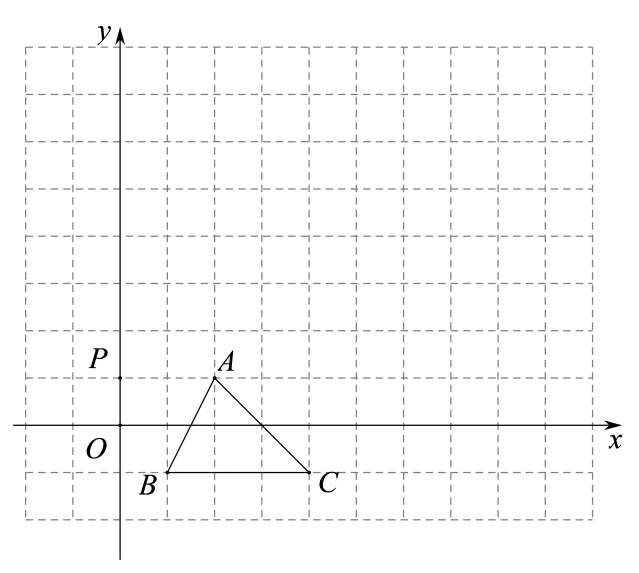下列问题：

(1)、画出△ABC沿x轴向右平移1个单位长度，再沿y轴向上平移3个单位长度后的 $△ A_{1} B_{1} C_{1}$ ，其中，点A的对应点是点 $A_{1}$ ，点B的对应点是点 $B_{1}$ ；

(2)、在第一象限内，以点P为位似中心，画出 $△ A_{2} B_{2} C_{2}$ 使它与 $△ A_{1} B_{1} C_{1}$ 位似，且位似比为2，并直接写出点 $A_{1}$ 的对应点 $A_{2}$ 的坐标．

查看试题解析
18. 2022年2月4日第24届冬奥会在北京开幕，某礼品销售商以每件8元的价格购进冬奥会纪念品，以每件10元的价格出售，每天可售出200件．销售商想采用提高售价的办法来增加利润．经试验，发现这种纪念品每件的售价每提高1元，每天的销售量就会减少10件，销售这种纪念品每天获得利润为1050元，求售价是多少元．

查看试题解析
19. 随着“双减”和“双增”政策的落实．某校为充分调动学生的积极性，在学校开展各项娱乐活动，丰富学生的课余生活，其中，语文组开展了以“说我身边的事”为主题的演讲比赛，共有5位同学获得一等奖，其中，七年级1位，八、九年级各2位．

(1)、从获得一等奖的5位同学中随机抽取1位参加区级比赛，则抽到八年级学生的概率是；

(2)、学校决定从获得一等奖的同学中任选2位同学参加社区组织的“说我身边的变化”演讲活动．请用列表或画树状图方法求所选2位同学中，恰好是1位七年级同学和1位九年级同学的概率．

查看试题解析
20. 我国铅球运动员巩立姣在2021年8月1日东京奥运会铅球比赛中以20.53米的成绩力压群雄夺得冠军．如图是在她的一次赛前训练中，铅球行进高度y（米）与水平距离x（米）之间存在的函数关系式是 $y = - \frac{1}{12} x^{2} + \frac{19}{12} x + \frac{5}{3}$ ．求：

(1)、这次训练中，巩立姣推铅球的成绩是多少米；

(2)、铅球距离地面的最大高度为多少米．

查看试题解析
21. 如图，有一栋楼房要安装电梯，由于楼前有低矮的物体，因此不能直接测量这栋楼AB的高度，测量人员在点C处测得该楼的楼顶A的仰角为20°，前进40米到达D处，测得楼顶A的仰角为45°测倾仪 $C M = D N = 1.5$ 米，且CM、DN及AB在同一平面内．求这栋楼AB的高度．（参考数据： $s i n 20 ° \approx 0.34$ ， $c o s 20 ° \approx 0.94$ ， $t a n 20 ° \approx 0.36$ ）

查看试题解析
22. 综合与探究
问题情境：

如图，正方形ABCD的边长为12，点E在BC边上运动．

(1)、探究发现：
如图1，当 $B E = 5$ 时，连接AE，过点B作 $B F ⊥ A E$ 于点G，交CD于点F，请直接写出线段BG和BF的长度；

(2)、如图2，以BE为边作正方形BEFG，并把正方形BEFG绕点B逆时针旋转，连接AG和DF，发现DF与AG之间存在数量关系，请写出它们的数量关系并证明．

(3)、探究拓广：
如图3，点E运动到与点C重合，连接AC，在AB上取点F，使 $A F = 8$ ，以CF为边作正方形CFMN，连接AM，在图3中补全图形并直接写出AM的长．

查看试题解析
23. 综合与实践
如图，抛物线y= $\frac{4}{3}$ x²+bx+c与x轴交于A（−1，0），B两点（点B在点A的右侧），与y轴交于点C（0，−4）．

(1)、求抛物线的解析式及顶点E的坐标；

(2)、如图，点H是抛物线上的动点，且△OCH的面积是8，求点H的坐标；

(3)、点D在抛物线上，连接ED交直线BC与点G，当DG=2GE时，直接写出点D的坐标．

查看试题解析