山西省晋城市阳城县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-10-28 类型:期末考试
一、单选题
-
1. 估计 +1的值应在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间2. 下列计算正确的是( )A、 B、 C、 D、3. 若关于x的方程(m﹣1)x2+mx﹣1=0是一元二次方程,则m的取值范围是( )A、m≠1 B、m=1 C、m≥1 D、m≠04. 投掷一枚正六面体骰子,“掷得的数是奇数”这一事件是( )A、必然事件 B、不可能事件 C、确定事件 D、随机事件5. 如图,△ABC与△DEF位似,点O是它们的位似中心,其中OE=2OB,则△ABC与△DEF的周长之比是( )
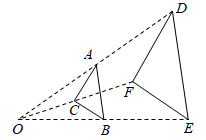 A、1:2 B、1:4 C、1:3 D、1:96. 如果关于x的一元二次方程(m-1)x2+2x+1=0有两个不相等的实数根,那么m的取值范围是( )A、m>2 B、m<2 C、m>2且m≠1 D、m<2且m≠17. 某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的实验最有可能的是( )
A、1:2 B、1:4 C、1:3 D、1:96. 如果关于x的一元二次方程(m-1)x2+2x+1=0有两个不相等的实数根,那么m的取值范围是( )A、m>2 B、m<2 C、m>2且m≠1 D、m<2且m≠17. 某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的实验最有可能的是( ) A、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” B、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 C、暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球 D、掷一个质地均匀的正六面体骰子,向上的面点数是68. 如图,学校课外生物小组的试验园地的形状是长35米、宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为600平方米,则小道的宽为多少米?若设小道的宽为 米,则根据题意,列方程为( )
A、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” B、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 C、暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球 D、掷一个质地均匀的正六面体骰子,向上的面点数是68. 如图,学校课外生物小组的试验园地的形状是长35米、宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为600平方米,则小道的宽为多少米?若设小道的宽为 米,则根据题意,列方程为( ) A、 B、 C、 D、9. 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
A、 B、 C、 D、9. 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )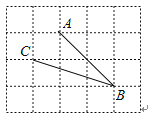 A、2 B、 C、 D、10. 如图,在 ABC中,点D在AB边上,点E在BC边上,过点D作DG BC , 交AC于点G , 过点E作EH AB , 交AC于点H , DG的延长线与EH的延长线交于点F , 则下列式子一定正确的是( )
A、2 B、 C、 D、10. 如图,在 ABC中,点D在AB边上,点E在BC边上,过点D作DG BC , 交AC于点G , 过点E作EH AB , 交AC于点H , DG的延长线与EH的延长线交于点F , 则下列式子一定正确的是( )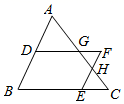 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 二次根式的值是12. 化简的结果是 .13. 已知: , 则= .14. 不解方程,求出方程的两根之和与两根之积是、 .15. 与相似,的对应边的面积为10.则的面积是 .16. 某市民政部门举行“即开式福利彩票”销售活动,发行彩票10万张(每张彩票2元),在这些彩票中,设置如下奖项:
奖金(元)
10000
5000
1000
500
100
50
数量(个)
1
4
20
40
100
200
如果花2元购买1张彩票,那么所得奖金不少于1000元的概率是
17. 某厂家2020年1~5月份的口罩产量统计如图所示,设从2月份到4月份,该厂家口罩产量的月平均增长率为 ,根据题意可得方程 .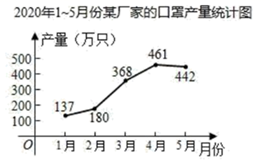 18. 如图,在 中,点D , E分别是 的中点, 与 相交于点F , 若 ,则 的长是 .
18. 如图,在 中,点D , E分别是 的中点, 与 相交于点F , 若 ,则 的长是 .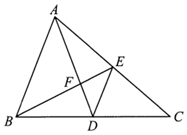 19. 如图,一段河坝的断面为梯形 , 根据图中的数据,求得的坡角a和坝底宽分别为、 .
19. 如图,一段河坝的断面为梯形 , 根据图中的数据,求得的坡角a和坝底宽分别为、 . 20. 如图,在中, , 垂足为D,点E是边的中点, , 则的长为 .
20. 如图,在中, , 垂足为D,点E是边的中点, , 则的长为 .
三、解答题
-
21. 解方程及求值:(1)、(2)、(用配方法解)(3)、(用公式法解)(4)、22. 如图,在△ABC中,点D在AB边上,∠ABC=∠ACD.
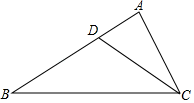 (1)、求证:△ABC∽△ACD;(2)、若AD=2,AB=8,求AC的长.23. 在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)、求证:△ABC∽△ACD;(2)、若AD=2,AB=8,求AC的长.23. 在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).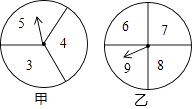 (1)、请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;(2)、分别求出李燕和刘凯获胜的概率.24. 为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如下图,一对搜寻人员以3.6公里/小时的速度在森林中搜寻,当他们行驶到A处时,发现在他们的东北方向有一古树B.他们继续向北行走40分钟后到达C处,发现古树B在他们的北偏东方向,求此时他们与古树B的距离(结果精确到0.1公里,参考数据:).
(1)、请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;(2)、分别求出李燕和刘凯获胜的概率.24. 为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如下图,一对搜寻人员以3.6公里/小时的速度在森林中搜寻,当他们行驶到A处时,发现在他们的东北方向有一古树B.他们继续向北行走40分钟后到达C处,发现古树B在他们的北偏东方向,求此时他们与古树B的距离(结果精确到0.1公里,参考数据:). 25. 为了提高市民对创建文明城市工作的支持,县文明办在兰花社,区开展“创文”宣传工作,据了解该社区共有居民18000人,分两个区域,兰花A区居民数量不超过兰花B区居民数量的3倍.(1)、求兰花B区至少有多少人;(2)、通过调查发现:前期志愿者在两个区域宣传“创文”工作的居民人数分别为1500人和2700人.为提高居民对“创文”工作的支持,志愿者利用两个月的时间加强社区人户宣传,兰花A区居民了解“创文”工作的人数月平均增长率为m;兰花B区居民了解“创文”工作的人数两个月的增长率为 . 两个月后该社区居民了解“创文”工作的人数达到 . 求m的值.26. 综合与实践
25. 为了提高市民对创建文明城市工作的支持,县文明办在兰花社,区开展“创文”宣传工作,据了解该社区共有居民18000人,分两个区域,兰花A区居民数量不超过兰花B区居民数量的3倍.(1)、求兰花B区至少有多少人;(2)、通过调查发现:前期志愿者在两个区域宣传“创文”工作的居民人数分别为1500人和2700人.为提高居民对“创文”工作的支持,志愿者利用两个月的时间加强社区人户宣传,兰花A区居民了解“创文”工作的人数月平均增长率为m;兰花B区居民了解“创文”工作的人数两个月的增长率为 . 两个月后该社区居民了解“创文”工作的人数达到 . 求m的值.26. 综合与实践问题情境:数学课上,老师出示了这样一个问题:如图①,在四边形中, , 对角线相交于点O.

求证:;
(1)、独立思考:请解答老师提出的问题;(2)、实践探究:求证:;小明最近迷上了思维导图,他运用思维导图使解题思维、化归过程显性化,请帮助小明完成解题思路、化归过程分析的思维导图:(3)、问题解决:智慧小组在题中增加条件“延长相交于点E”,如图②.求证: .