浙江省精诚联盟2022-2023学年高二上学期数学10月联考试卷
试卷更新日期:2022-10-28 类型:月考试卷
一、单选题
-
1. 直线的倾斜角是( )A、 B、 C、 D、2. 如图,在平行六面体中,设 , 则( )
 A、 B、 C、 D、3. 过点的直线与连接的线段总有公共点(不包含端点),则直线的斜率的取值范围是( )A、 B、 C、 D、4. 下列四个正方体图形中,分别为正方体的顶点或其所在棱的中点,能得出平面的图形是( )A、
A、 B、 C、 D、3. 过点的直线与连接的线段总有公共点(不包含端点),则直线的斜率的取值范围是( )A、 B、 C、 D、4. 下列四个正方体图形中,分别为正方体的顶点或其所在棱的中点,能得出平面的图形是( )A、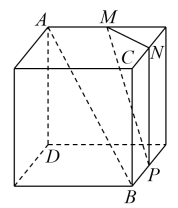 B、
B、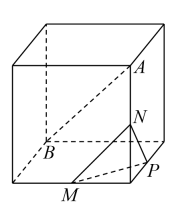 C、
C、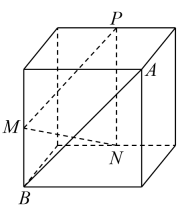 D、
D、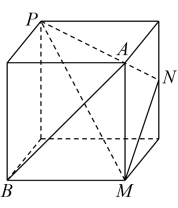 5. 一条光线从点射出,经直线反射后经过点 , 则反射光线所在直线的方程为( )A、 B、 C、 D、6. 在正四面体中,分别为和的中点,则异面直线与所成角的余弦值为( )A、 B、 C、 D、7. 已知圆经过三点 , 则点到圆上任意一点的距离的最小值是( )A、 B、 C、 D、8. 如图,在四棱锥中,底面是矩形,侧面是等腰直角三角形,平面平面 , 当棱上一动点到直线的距离最小时,过做截面交于点 , 则四棱锥的体积是( )
5. 一条光线从点射出,经直线反射后经过点 , 则反射光线所在直线的方程为( )A、 B、 C、 D、6. 在正四面体中,分别为和的中点,则异面直线与所成角的余弦值为( )A、 B、 C、 D、7. 已知圆经过三点 , 则点到圆上任意一点的距离的最小值是( )A、 B、 C、 D、8. 如图,在四棱锥中,底面是矩形,侧面是等腰直角三角形,平面平面 , 当棱上一动点到直线的距离最小时,过做截面交于点 , 则四棱锥的体积是( )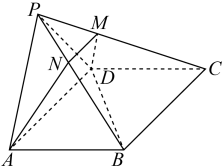 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 已知圆的一般方程为 , 则下列说法正确的是( )A、圆的圆心为 B、圆的半径为5 C、点不在圆上 D、圆关于对称10. 已知空间向量 , , 则下列说法正确的是( )A、向量与、垂直 B、向量与、共面 C、若与分别是异面直线与的方向向量,则其所成的角的余弦值为 D、向量在向量上的投影向量为11. 如图所示,边长为的等边从起始位置(与轴重合)绕着点顺时针旋转至与轴重合得到 , 在旋转的过程中,下列说法正确的是( )
 A、边所在直线的斜率的取值范围是 B、边所在直线在轴上截距的取值范围是 C、边与边所在直线的交点为 D、当的中垂线为时,12. 已知是正方体的中心,过点的直线与该正方体的表面交于、两点,下列叙述正确的有( )A、点、到正方体个表面的距离分别为、 , 则为定值 B、线段在正方体个表面的投影长度为 , 则为定值 C、正方体个顶点到直线的距离分别为 , 则为定值 D、直线与正方体条棱所成的夹角的 , 则为定值
A、边所在直线的斜率的取值范围是 B、边所在直线在轴上截距的取值范围是 C、边与边所在直线的交点为 D、当的中垂线为时,12. 已知是正方体的中心,过点的直线与该正方体的表面交于、两点,下列叙述正确的有( )A、点、到正方体个表面的距离分别为、 , 则为定值 B、线段在正方体个表面的投影长度为 , 则为定值 C、正方体个顶点到直线的距离分别为 , 则为定值 D、直线与正方体条棱所成的夹角的 , 则为定值三、填空题
-
13. 已知向量若 , 则.14. 已知直线则与的距离.15. 点到直线的距离最大时,.16. 在正三棱锥中, , 为的中点,为上靠近的三等分点,在平面上,且满足 , 在的边界上运动,则直线与所成角的余弦值的取值范围是.
四、解答题
-
17. 求满足下列条件的直线的一般式方程:(1)、经过直线的交点 , 且经过点;(2)、与直线垂直,且点到直线的距离为.18. 如图,在直三棱柱中,是等腰直角三角形, , 点分别是的中点,求证:
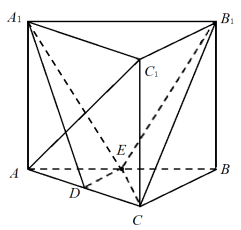 (1)、平面;(2)、平面.19. 已知动点与两个定点的距离的比为2.(1)、求动点的轨迹方程,并说明轨迹的形状;(2)、已知 , 求的最大值.
(1)、平面;(2)、平面.19. 已知动点与两个定点的距离的比为2.(1)、求动点的轨迹方程,并说明轨迹的形状;(2)、已知 , 求的最大值.