辽宁省大连部分重点高中2022-2023学年高二上学期数学10月月考试卷

试卷更新日期：2022-10-28 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知 $\vec{a} =$ （2，﹣1，2）， $\vec{b} =$ （x，y，6）， $\vec{a}$ 与 $\vec{b}$ 共线，则x+y＝（）

A、5 B、6 C、3 D、9

查看试题解析
2. 若直线l的方向向量 $\vec{a} = (1 ， 0 ， 1)$ ，平面 $β$ 的法向量 $\vec{n} = (1 ， 1 ， - 1)$ ，则（）

A、 $l \subset β$ B、 $l ⊥ β$ C、 $l / / β$ D、 $l \subset β$ 或 $l / / β$

查看试题解析
3. 若 ${\vec{a} ， \vec{b} ， \vec{c}}$ 构成空间的一组基底，则下列向量不共面的是（）

A、 $\vec{a} + \vec{b}$ ， $\vec{a} - \vec{b}$ ， $\vec{b}$ B、 $\vec{a} - \vec{b}$ ， $\vec{a} - \vec{b} + \vec{c}$ ， $- \vec{c}$ C、 $\vec{a} + 2 \vec{b}$ ， $\vec{a} - 2 \vec{b}$ ， $\vec{a} + \vec{c}$ D、 $\vec{a} - 2 \vec{b}$ ， $4 \vec{b} - 2 \vec{a}$ ， $\vec{a} + \vec{c}$

查看试题解析
4. 已知 $\vec{a}$ 、 $\vec{b}$ 都是空间向量，且 $⟨ \vec{a} ， \vec{b} ⟩ = \frac{2 π}{3}$ ，则 $⟨ 2 \vec{a} ， - 3 \vec{b} ⟩ =$ （）

A、 $\frac{π}{3}$ B、 $\frac{π}{6}$ C、 $\frac{2 π}{3}$ D、 $\frac{5 π}{6}$

查看试题解析
5. 如图，在平行六面体ABCD-A₁B₁C₁D₁中，AC与BD的交点为点M， $\vec{A B}$ ＝ $\vec{a}$ ， $\vec{A D}$ $= \vec{b}$ ， $\vec{A A_{1}}$ $= \vec{c}$ ，则下列向量中与 $\vec{C_{1} M}$ 相等的向量是（）

A、 $- \frac{1}{2} \vec{a} + \frac{1}{2} \vec{b} + \vec{c}$ B、 $\frac{1}{2} \vec{a} + \frac{1}{2} \vec{b} + \vec{c}$ C、 $- \frac{1}{2} \vec{a} - \frac{1}{2} \vec{b} - \vec{c}$ D、 $- \frac{1}{2} \vec{a} - \frac{1}{2} \vec{b} + \vec{c}$

查看试题解析
6. 已知大小为 $60 °$ 的二面角 $α - l - β$ 棱上有两点A、B， $A C \subset α$ ， $A C ⊥ l$ ， $B D \subset β$ ， $B D ⊥ l$ ，若 $A C = 3$ ， $B D = 3$ ， $C D = 7$ ，则 $A B$ 的长为（）

A、22 B、40 C、 $2 \sqrt{10}$ D、 $\sqrt{22}$

查看试题解析
7. 如图，在边长为 $3$ 的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $P$ 是棱 $A B$ 上一点且 $A P = 1$ ， $M$ 是面 $B_{1} B C C_{1}$ 上的点.一质点从点 $P$ 射向点 $M$ ，遇到正方体的面反射（反射服从光的反射原理），反射到点 $D_{1}$ ，则线段 $P M$ 与 $M D_{1}$ 的长度之和为（）

A、 $\sqrt{6} + \sqrt{17}$ B、 $3 + \sqrt{14}$ C、 $\sqrt{43}$ D、 $5 \sqrt{2}$

查看试题解析
8. 如图，在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，侧棱 $A A_{1} ⊥$ 底面 $A_{1} B_{1} C_{1}$ ， $∠ B A C = 90 ° ， A B = A C = A A_{1} = 1 ， D$ 是棱 $C C_{1}$ 的中点， $P$ 是 $A D$ 的延长线与 $A_{1} C_{1}$ 的延长线的交点.若点 $Q$ 在直线 $B_{1} P$ 上，则下列结论正确的是

A、当点 $Q$ 为线段 $B_{1} P$ 的中点时， $D Q ⊥$ 平面 $A_{1} B D$ B、当点 $Q$ 为线段 $B_{1} P$ 的三等分点时， $D Q ⊥$ 平面 $A_{1} B D$ C、在线段 $B_{1} P$ 的延长线上，存在一点 $Q$ ，使得 $D Q ⊥$ 平面 $A_{1} B D$ D、不存在点 $Q$ ，使 $D Q$ 与平面 $A_{1} B D$ 垂直

查看试题解析

二、多选题

9. 已知空间中三点 $A (0, 1, 0)$ ， $B (2, 2, 0)$ ， $C (- 1, 3, 1)$ ，则下列说法正确的是（）

A、 $\vec{A B}$ 与 $\vec{A C}$ 是共线向量 B、与 $\vec{A B}$ 同向的单位向量是 $(\frac{2 \sqrt{5}}{5}, \frac{\sqrt{5}}{5}, 0)$ C、 $\vec{A B}$ 和 $\vec{B C}$ 夹角的余弦值是 $\frac{\sqrt{55}}{11}$ D、平面 $A B C$ 的一个法向量是 $(1, - 2, 5)$

查看试题解析
10. 过 $△ A B C$ 所在平面 $α$ 外一点P，作 $P O ⊥ α$ ，垂足为 $O$ ， .以下推断正确的是（）

A、若 $P A ⊥ B C$ ， $P B ⊥ A C$ ，则点 $O$ 是 $△ A B C$ 的垂心 B、若 $P A = P B = P C$ ，则点 $O$ 是 $△ A B C$ 的外心 C、若 $∠ P A B = ∠ P A C$ ， $∠ P B A = ∠ P B C$ ，则点 $O$ 是 $△ A B C$ 的内心 D、过点 $P$ 分别作边 $A B ， B C ， A C$ 的垂线，垂足分别为 $E ， F ， G$ ，若 $P E = P F = P G$ ，则点 $O$ 是 $△ A B C$ 的重心

查看试题解析
11. 在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，E、F、G分别为BC、 $C C_{1}$ 、 $B B_{1}$ 的中点，则下列选项正确的是（）

A、 $D_{1} D ⊥ A F$ B、直线 $A_{1} G$ 与EF所成角的余弦值为 $\frac{\sqrt{10}}{10}$ C、三棱锥 $G - A E F$ 的体积为 $\frac{1}{3}$ D、存在实数 $λ$ 、 $μ$ 使得 $\vec{A_{1} G} = λ \vec{A F} + μ \vec{A E}$

查看试题解析
12. 如图，长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = 2$ ， $A D = 1$ ， $A A_{1} = 3$ ，点M是侧面 $A D D_{1} A_{1}$ 上的一个动点（含边界），P是棱 $C C_{1}$ 的中点，则下列结论正确的是（）

A、当PM长度最小时，三棱锥 $M - B D P$ 的体积为 $\frac{1}{2}$ B、当PM长度最大时，三棱锥 $M - B D P$ 的体积为 $\frac{1}{2}$ C、若保持 $P M = \sqrt{5}$ ，则点M在侧面内运动路径的长度为 $π$ D、若M在平面 $A D D_{1} A_{1}$ 内运动，且 $∠ M D_{1} B = ∠ B_{1} D_{1} B$ ，则点M的轨迹为圆弧

查看试题解析

三、填空题

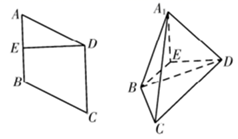
13. $\vec{a} = (1 ， - 1 ， 3)$ ， $\vec{b} = (- 1 ， 4 ， - 2)$ ， $\vec{c} = (1 ， 5 ， x)$ ，若 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ 三向量共面，则实数 $x =$ .

查看试题解析
14. 正四面体ABCD的棱长为2，点E，F，G分别是棱AB，AD，DC的中点，则 $\vec{G E} \cdot \vec{G F}$ 的值为．

查看试题解析
15. 如图，在菱形 $A B C D$ 中， $A B = 2$ ， $∠ D A B = 60 °$ ， $E$ 是 $A B$ 的中点，将 $△ A D E$ 沿直线 $D E$ 翻折至 $△ A_{1} D E$ 的位置，使得面 $A_{1} E D ⊥$ 面 $B C D E$ ，则点 $A_{1}$ 到直线 $D B$ 的距离为.

查看试题解析
16. 在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，已知 $A A_{1} = A B = 2 A D = 2$ ， E、F分别为 $B B_{1}$ 、 $D_{1} C_{1}$ 的中点，则三棱锥 $C_{1} - C E F$ 的外接球半径为，平面 $A_{1} B C D_{1}$ 被三棱锥 $C_{1} - C E F$ 外接球截得的截面圆面积为．

查看试题解析

四、解答题

17.

(1)、已知 $\vec{a} = (1 ， 2 ， - y)$ ， $\vec{b} = (x ， 1 ， 2)$ ，且 $(\vec{a} + 2 \vec{b}) / / (2 \vec{a} - \vec{b})$ ，求 $x$ ， $y$ 的值；

(2)、已知 $A (2 ， 0 ， 0)$ ， $B (0 ， - 1 ， 1)$ ，若 $\vec{O A} + λ \vec{O B}$ 与 $\vec{O B}$ （ $O$ 为坐标原点）的夹角为 $60 °$ ，求 $λ$ 的值.

查看试题解析
18. 如图，在三棱锥 $A - B C D$ 中， $C D ⊥$ 平面ABC， $A C = C B = \frac{1}{2} C D$ ， $∠ A C B = 90 °$ ，点E，F分别是AB，AD的中点.

(1)、求证： $A C ⊥$ 平面BCD；

(2)、设 $A C = C B = 2$ ，求直线AD与平面CEF所成角的正弦值

查看试题解析
19. 如图所示，在四棱锥 $P - A B C D$ 中， $△ P B C$ 为等腰直角三角形，且 $∠ C P B = 90 °$ ，四边形ABCD为直角梯形，满足 $A D / / B C$ ， $C D ⊥ A D$ ， $B C = C D = 2 A D = 4$ ， $P D = 2 \sqrt{6}$ ．

(1)、若点F为DC的中点，求 $c o s ⟨ \vec{A P} ， \vec{B F} ⟩$ ；

(2)、若点E为PB的中点，点M为AB上一点，当 $\vec{E M} ⊥ \vec{B F}$ 时，求 $\frac{| \vec{A M} |}{| \vec{A B} |}$ 的值．

查看试题解析
20. 在① $(\vec{D E} + \vec{C F}) ⊥ (\vec{D E} - \vec{C F})$ ， ② $| \vec{D E} | = \frac{\sqrt{1} \hat{7}}{2}$ ， ③ $0 < c o s ⟨ \vec{E F} ， \vec{D B} ⟩ < 1$ 这三个条件中任选一个，补充在下面的问题中.
问题：如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，以D为坐标原点，建立空间直角坐标系D-xyz.已知点 $D_{1}$ 的坐标为 $(0 ， 0 ， 2)$ ， E为棱 $D_{1} C_{1}$ 上的动点，F为棱 $B_{1} C_{1}$ 上的动点，________，试问是否存在点E，F满足 $\vec{E F} \cdot \vec{A_{1} C} = 0$ 若存在，求 $\vec{A E} \cdot \vec{B F}$ 的值；若不存在，请说明理由注：如果选择多个条件分别解答，按第一个解答计分.

查看试题解析
21. 如图，已知正方形 $A B C D$ 和矩形 $A C E F$ 所在的平面互相垂直， $A B = \sqrt{2}$ ， $A F = t$ ， $M$ 是线段 $E F$ 的中点．

(1)、求证： $A M / /$ 平面 $B D E$ ；

(2)、若 $t = 1$ ，求平面 $A D F$ 与平面 $D F B$ 所成角；

(3)、若线段 $A C$ 上总存在一点 $P$ ，使得 $P F ⊥ B E$ ，求 $t$ 的最大值．

查看试题解析
22. 如图多面体 $A B C D E F$ 中，四边形 $A B C D$ 是菱形， $∠ A B C = 60 °$ ， $E A ⊥$ 平面 $A B C D$ ， $E A / / B F$ ， $A B = A E = 2 B F = 2$

(1)、证明：平面 $E A C ⊥$ 平面 $E F C$ ；

(2)、在棱 $E C$ 上有一点 $M$ ，使得平面 $M B D$ 与平面 $A B C D$ 的夹角为 $45 °$ ，求点 $M$ 到平面 $B C F$ 的距离.

查看试题解析