湖南省长沙市八校联考2022-2023学年高二上学期数学第一次月考试卷
试卷更新日期:2022-10-28 类型:月考试卷
一、单选题
-
1. 函数 的零点的个数为 ( )A、0 B、1 C、2 D、32. 四个函数:① ;② ;③ ;④ 的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是( )
 A、④①②③ B、①④②③ C、③④②① D、①④③②3. 已知锐角三角形ABC的内角A,B,C的对边分别为 , 且 , 则的取值范围是( )A、 B、 C、 D、4. 古希腊数学家阿基米德的墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,据说阿基米德对这个图最引以为自豪,则该圆柱的体积与球的体积之比为( )A、 B、 C、 D、5. 已知函数在区间上有且只有一个零点,则正实数的取值范围是( )A、 B、 C、 D、6. 已知 为正三角形 内一点,且满足 ,若 的面积与 的面积之比为3,则 ( )A、 B、 C、 D、7. 三边 ,满足 ,则三角形 是( )A、锐角三角形 B、钝角三角形 C、等边三角形 D、直角三角形8. 已知实数 满足 ,则 的最大值为( )A、 B、 C、 D、
A、④①②③ B、①④②③ C、③④②① D、①④③②3. 已知锐角三角形ABC的内角A,B,C的对边分别为 , 且 , 则的取值范围是( )A、 B、 C、 D、4. 古希腊数学家阿基米德的墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,据说阿基米德对这个图最引以为自豪,则该圆柱的体积与球的体积之比为( )A、 B、 C、 D、5. 已知函数在区间上有且只有一个零点,则正实数的取值范围是( )A、 B、 C、 D、6. 已知 为正三角形 内一点,且满足 ,若 的面积与 的面积之比为3,则 ( )A、 B、 C、 D、7. 三边 ,满足 ,则三角形 是( )A、锐角三角形 B、钝角三角形 C、等边三角形 D、直角三角形8. 已知实数 满足 ,则 的最大值为( )A、 B、 C、 D、二、多选题
-
9. 已知函数 , 若 , 则的值可能为( )A、1 B、 C、10 D、10. 八卦是中国文化的基本哲学概念,如图1船八卦模型图,其平面图形记为图2中的正八边形 , 其中 , 则下列结论正确的有( )
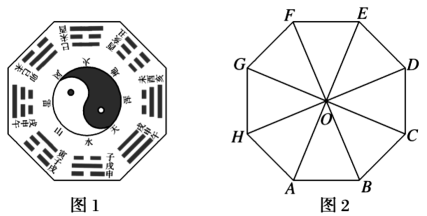 A、 B、 C、 D、在向量上的投影为11. 定义行列式 , 若函数 , 则下列表述错误的是( )A、的图象关于点中心对称 B、的图象关于直线对称 C、在区间上单调递增 D、是最小正周期为的奇函数12. 如图,在三棱锥中,、、分别为棱、、的中点,平面 , , , , 则( )
A、 B、 C、 D、在向量上的投影为11. 定义行列式 , 若函数 , 则下列表述错误的是( )A、的图象关于点中心对称 B、的图象关于直线对称 C、在区间上单调递增 D、是最小正周期为的奇函数12. 如图,在三棱锥中,、、分别为棱、、的中点,平面 , , , , 则( ) A、点与点到平面的距离相等 B、直线与直线垂直 C、三棱锥的体积为18 D、平面截三棱锥所得的截面面积为12
A、点与点到平面的距离相等 B、直线与直线垂直 C、三棱锥的体积为18 D、平面截三棱锥所得的截面面积为12三、填空题
-
13. 某学校10位同学组成的志愿者组织分别由李老师和张老师负责,每次献爱心活动均需该组织2位同学参加.假设李老师和张老师分别将各自活动通知的信息独立,随机地发给2位同学,且所发信息都能收到,则甲同学收到李老师或张老师所发活动通知的信息的概率为 .14. 函数的值域是.15. 已知 , 且 , 若不等式恒成立,则实数的最大值是.16. 如图,在棱长为2的正方体中 , 点是的中点,动点在底面内(包括边界),若平面 , 则与底面所成角的正弦的取值范围是 .

四、解答题
-
17. 已知集合 , 集合 , 集合.(1)、求;(2)、若 , 求实数的值取范围.18. 设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,
(Ⅰ)求B的大小;
(Ⅱ)若 , 求的取值范围.19. 设函数 , 其中.(1)、求函数的值域;(2)、若 , 讨论在区间上的单调性;(3)、若在区间上为增函数,求的最大值.
