（浙教版）2022-2023学年九年级数学下册3.4简单几何体的表面展开图同步测试

试卷更新日期：2022-10-27 类型：同步测试

进入出卷网下载

一、单选题

1. 如图是一个正方体的表面展开图，则原正方体中与“河”字所在的面相对的面上标的字是（）

A、建 B、设 C、美 D、丽

查看试题解析
2. 一个圆锥的主视图是边长为6cm的正三角形，则这个圆锥的侧面积等于（　　）

A、36 πcm² B、24πcm² C、18πcm² D、12 πcm²

查看试题解析
3. 若圆锥的主视图是边长为 $4 c m$ 的等边三角形，则该圆锥俯视图的面积是（）

A、 $4 π c m^{2}$ B、 $8 π c m^{2}$ C、 $12 π c m^{2}$ D、 $16 π c m^{2}$

查看试题解析
4. 用半径为6的半圆围成一个圆锥的侧面，则圆锥的底面半径等于（）

A、3 B、 $\frac{5}{2}$ C、2 D、 $\frac{3}{2}$

查看试题解析
5.
如图是一个正方体的展开图，把展开图折叠成正方体后，有“弘”字一面的相对面上的字是（）

A、传 B、统 C、文 D、化

查看试题解析
6. 如图，已知圆柱的底面直径BC= $\frac{6}{π}$ ，高AB=3，小虫在圆柱表面爬行，从C点爬到A点，然后再沿另一面爬回C点，则小虫爬行的最短路程为（）

A、 $3 \sqrt{2}$ B、 $3 \sqrt{5}$ C、 $6 \sqrt{5}$ D、 $6 \sqrt{2}$

查看试题解析
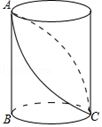7. 如果圆锥的母线长为5cm，底面半径为2cm，那么这个圆锥的侧面积为（）

A、10cm² B、10πcm² C、20cm² D、20πcm²

查看试题解析
8. 如图是一个几何体的三视图，则这个几何体的侧面积是（）

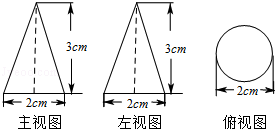A、 πcm² B、2 πcm² C、6πcm² D、3πcm²

查看试题解析
9. 已知圆锥的母线长为6cm，底面圆的半径为3cm，则此圆锥侧面展开图的圆心角是（）

A、30° B、60° C、90° D、180°

查看试题解析
10. 若圆锥的侧面展开图是一个半径为a的半圆，则圆锥的高为（）

A、a B、 $\frac{\sqrt{3}}{3}$ a C、3a D、 $\frac{\sqrt{3}}{2} a$

查看试题解析

二、填空题

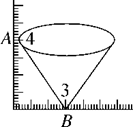
11. 一个圆锥的底面半径r=10，高h=20，则这个圆锥的侧面积是

查看试题解析
12. 若圆锥的底面半径为5，高为12，则圆锥的侧面展开图的面积是.

查看试题解析
13. 已知圆锥的底面半径为5cm，母线长为13cm，则这个圆锥的侧面积是.

查看试题解析
14. 已知圆锥的底面半径为 $5 cm$ ，侧面展开图的圆心角是180°，则圆锥的高是 $cm$ ．

查看试题解析
15. 一个圆锥形漏斗，某同学用三角板测得其高度的尺寸如图所示，则该圆锥形漏斗的侧面积为.

查看试题解析

三、解答题

16. 一个盖着瓶盖的瓶子里面装着一些水（如下图所示），请你根据图中标明的数据，计算瓶子的容积．

查看试题解析
17. 如图是一个立体图形的三视图，请根据视图写出该立体图形的名称，并计算该立体图形的体积（结果保留π）．

查看试题解析
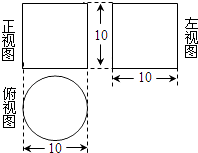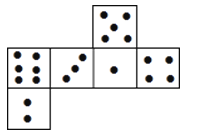
18.
如图是一个正方体骰子的表面展开图，请根据要求回答问题：
（1）如果1点在上面，3点在左面，几点在前面？
（2）如果5点在下面，几点在上面？

查看试题解析
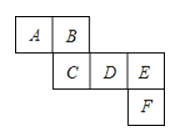
19.
如图是一个正方体的表面展开图，请回答下列问题：
（1）与面B、C相对的面分别是？
（2）若A=a³+a²b+3，B=a²b﹣3，C=a³﹣1，D=﹣（a²b﹣6），且相对两个面所表示的代数式的和都相等，求E、F分别代表的代数式．

查看试题解析
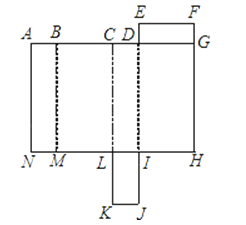
20.
如图所示是长方体的表面展开图，折叠成一个长方体．
（1）与字母F重合的点有哪几个？
（2）若AD=4AB，AN=3AB，长方形DEFG的周长比长方形ABMN的周长少8，求原长方体的容积．

查看试题解析
21. 如图所示，已知圆锥底面半径r=10cm，母线长为40cm．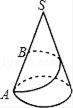

(1)、求它的侧面展开图的圆心角和表面积．

(2)、若一甲出从A点出发沿着圆锥侧面行到母线SA的中点B，请你动脑筋想一想它所走的最短路线是多少？为什么？

查看试题解析
22. 如图1，一个边长为2cm的立方体按某种方式展开后，恰好能放在一个长方形内．

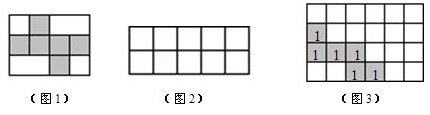(1)、计算图1长方形的面积；

(2)、小明认为把该立方体按某种方式展开后可以放在如图2的长方形内，请你在图2中划出这个立方体的表面展开图；(图2每个小正方形边长为2cm)；

(3)、如图3，在长12cm、宽8cm的长方形内已经画出该立方体的一种表面展开图(各个面都用数字“1”表示)，请你在剩下部分再画出2个该立方体的表面展开图，把一个立方体的每一个面标记为“2”，另一个立方体的每一个面标记为“3”．

查看试题解析
23.
小明在学习了《展开与折叠》这一课后，明白了很多几何体都能展开成平面图形．于是他在家用剪刀展开了一个长方体纸盒，可是一不小心多剪了一条棱，把纸盒剪成了两部分，即图中的①和②．根据你所学的知识，回答下列问题：

（1）小明总共剪开了多少条棱？

（2）现在小明想将剪断的②重新粘贴到①上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒，你认为他应该将剪断的纸条粘贴到①中的什么位置？请你帮助小明在①上补全．

（3）小明说：他所剪的所有棱中，最长的一条棱是最短的一条棱的5倍．现在已知这个长方体纸盒的底面是一个正方形，并且这个长方体纸盒所有棱长的和是880cm，求这个长方体纸盒的体积．

查看试题解析
24. 如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C.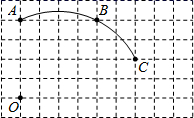

(1)、请完成如下操作：
①以点O为原点、竖直和水平方向所在的直线为坐标轴、网格边长为单位长，建立平面直角坐标系；②用直尺和圆规画出该圆弧所在圆的圆心D的位置（不用写作法，保留作图痕迹），并连接AD、CD.

(2)、请在（1）的基础上，完成下列问题：
①写出点的坐标：C ▲ 、D ▲ ；

②⊙D的半径= ▲ .（结果保留根号）；

③若扇形ADC是一个圆锥的侧面展开图，求该圆锥的底面面积. （结果保留π）

查看试题解析