（北师大版）2022-2023学年九年级数学下册第三章圆 单元测试
试卷更新日期：2022-10-27 类型：单元试卷
一、单选题（每题3分，共30分）
-
1. 点P在半径为r的⊙A外，则点P到点A的距离d与r的关系是（ ）A、d≤r B、d＜r C、d≥r D、d＞r2.
如图，已知AB是⊙O的直径，弦CD⊥AB于E，连接BC、BD、AC，下列结论中不一定正确的是（ ）
A、∠ACB=90° B、OE=BE C、BD=BC D、△BDE∽△CAE3. 《九章算术》是我国古代第一部自成体系的数学专著，代表了东方数学的最高成就．它的算法体系至今仍在推动着计算机的发展和应用．书中记载：“今有圆材埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”译为：“今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯这木材，锯口深1寸（ED=1寸），锯道长1尺（AB=1尺=10寸）”，问这块圆柱形木材的直径是多少？”如图所示，请根据所学知识计算：圆柱形木材的直径AC是（ ）
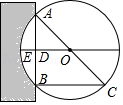A、13寸 B、20寸 C、26寸 D、28寸4. 如图，AB是⊙O的直径，弦CD交AB于点P，AP=2，BP=6，∠APC=30°，则CD的长为（ ）
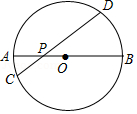A、
B、2 
C、2
D、8
5. 如图，四边形ABCD内接于 ，若∠BOD=144°，则∠C的度数是（ ）
A、14° B、36° C、72° D、108°6. 若点O是等腰△ABC的外心，且∠BOC=60°，底边BC=2，则△ABC的面积为（ ）A、2+ B、 C、4+2 或2﹣ D、2+ 或2﹣7. 如图，在平面直角坐标系中，⊙M与x轴相切于点A，与y轴交于B、C两点，M的坐标为(3，5)，则B的坐标为 （ ）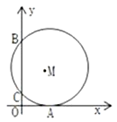
A、(0，5) B、(0，7) C、(0，8) D、(0，9)8. 正六边形的边心距与边长之比为（ ）
A、1 ： 2 B、：2 C、：1 D、：29. 如图，点A，B，C在半径为9的⊙O上，OA∥BC，∠OAB=70°，则弧AC的长为（ ）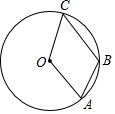
A、 B、 C、 D、10. 如图，一根6m长的绳子，一端拴在围墙墙角的柱子上，另一端拴着一只小羊A（羊只能在草地上活动）那么小羊A在草地上的最大活动区域面积是（ ）
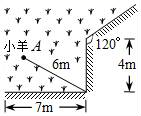A、9πm2 B、 πm2 C、15πm2 D、 πm2二、填空题（每题3分，共15分）
-
11. PA、PB切⊙O于A、B两点，CD切⊙O于点E，交PA、PB于C、D，若⊙O的半径为r，△PCD的周长等于3r，则tan∠APB的值是.
12. 如图，△ABC内接于半径为 的半圆O中，AB为直径，点M是 的中点，连结BM交AC于点E，AD平分∠CAB交BM于点D，∠ADB＝135°且D为BM的中点，则DM的长为 ；BC的长为 .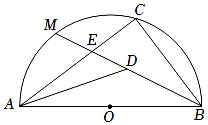
13. 如图，点 是上⊙O两点， ，点 是⊙O上的动点（ 与 不重合），连结 ，过点 分别作 于 ， 于 ，则 .
14. 如图，有公共顶点A、B的还五边形和正六边形，连接AC并延长交正六边形于点D，则∠ADE的度数为°.
15. 如图，AB是⊙O的切线，A为切点，OB=5 ，AB=5，AC是⊙O的弦，圆心到弦AC的距离为3，则弦AC的长为 ．
三、解答题（共8题，共55分）
-
16.
如图，AB、CD为⊙O中两条直径，点E、F在直径CD上，且CE=DF．
求证：AF=BE．
17.如图，某新建公园有一个圆形人工湖，湖中心O处有一座喷泉，小明为测量湖的半径，在湖边选择A、B两个点，在A处测得∠OAB=45°，在AB延长线上的C处测得∠OCA=30°，已知BC=50米，求人工湖的半径．（结果保留根号）
18.如图，已知△ABC内接于⊙O，AD、AE分别平分∠BAC和△BAC的外角∠BAF，且分别交圆于点D、F，连接DE，CD，DE与BC相交于点G．
（1）求证：DE是△ABC的外接圆的直径；
（2）设OG=3，CD= ， 求⊙O的半径．
19.如图，在△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作⊙O的切线，交AB于点E，交CA的延长线于点F．
（1）求证：FE⊥AB；
（2）当EF=6，时，求DE的长．
20. 已知：如图，过圆O外一点B作圆O的切线BM，M为切点，BO交圆O于点A，过点A作BO的垂线，交BM于点P，BO＝3，圆O的半径为1．求：MP的长.
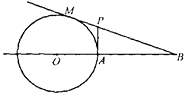21.如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2）、B（1，3）．
（1）画出△AOB绕点O逆时针旋转90°后得到的△A1OB1 ．
（2）填空：点A1的坐标为 ．
（3）求出在旋转过程中，线段OB扫过的扇形面积．
