（北师大版）2022-2023学年九年级数学下册3.8圆内接正多边形 同步测试
试卷更新日期：2022-10-27 类型：同步测试
一、单选题
-
1. 如图，⊙O的周长等于4πcm，则它的内接正六边形ABCDEF的面积是（ ）
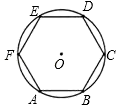A、 B、 C、 D、2. 同圆的内接正三角形与内接正方形的边长的比是（ ）A、
B、
C、
D、
3. 已知⊙O的面积为2π，则其内接正三角形的面积为（ ）A、3
B、3 
C、
D、
4. 如图，⊙O是正五边形ABCDE的外接圆，点P是 的一点，则∠CPD的度数是（ ）
A、30° B、36° C、45° D、72°5. 已知圆内接正三角形的面积为 ，则该圆的内接正六边形的边心距是（ ）A、2 B、1 C、
D、
6. 圆内接正六边形的边长为3，则该圆内接正三角形的边长为（ ）A、 B、 C、 D、7. 如图，正六边形ABCDEF，点P在直线AB上移动，若点P与正六边形六个顶点中的至少两个顶点距离相等，则直线AB上满足条件的点P共有（ ）
A、6个 B、5个 C、4个 D、3个8.如图，以正六边形ADHGFE的一边AD为边向外作正方形ABCD，则∠BED的度数为（ ）
A、30° B、45° C、50° D、60°9.如图，在正六边形ABCDEF中，△BCD的面积为4，则△BCF的面积为（ ）
A、16 B、12 C、8 D、610.如图，要拧开一个边长为a=6mm的正六边形螺帽，扳手张开的开口b至少为( )
A、6mm B、12mm C、6mm D、4mm二、填空题
-
11. 如图，正方形ABCD内接于⊙O，其边长为4，则⊙O的内接正三角形EFG的边长为 ．
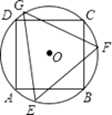12. 正n边形的边长与半径的夹角为75°，那么n= ．13. 如图，正六边形ABCDEF内接于⊙O，若⊙O的半径为4，则阴影部分的面积等于 ．
14. 如果正n边形的中心角是40°，那么n=.
15. 以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是。
三、解答题
-
16. 如图，四边形ABCD是⊙O的内接正方形，若正方形的面积等于4，求⊙O的面积．
17. 如图，已知等边△ABC，请用直尺（不带刻度）和圆规，按下列要求作图（不要求写作法，但要保留作图痕迹）：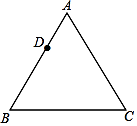
(1)、作△ABC的外心O；(2)、设D是AB边上一点，在图中作出一个正六边形DEFGHI，使点F，点H分别在边BC和AC上．18. 如图，正三角形ABC内接于⊙O，若AB= cm，求⊙O的半径．
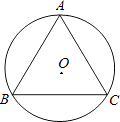19.如图，已知等边△ABC内接于⊙O，BD为内接正十二边形的一边，CD=5cm，求⊙O的半径R．
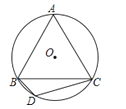20.如图，AG是正八边形ABCDEFGH的一条对角线．
（1）在剩余的顶点B、C、D、E、F、H中，连接两个顶点，使连接的线段与AG平行，并说明理由；
（2）两边延长AB、CD、EF、GH，使延长线分别交于点P、Q、M、N，若AB=2，求四边形PQMN的面积．
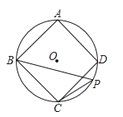
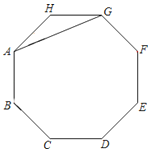21.如图，正方形ABCD的外接圆为⊙O，点P在劣弧上（不与C点重合）．
（1）求∠BPC的度数；
（2）若⊙O的半径为8，求正方形ABCD的边长．
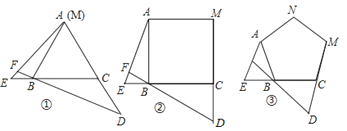
22.如图③，点E，D分别是正三角形ABC，正四边形ABCM，正五边形ABCMN中以点C为顶点的一边延长线和另一边反向延长线上的点，且△ABE与△BCD能相互重合，DB的延长线交AE于点F．
（1）在图①中，求∠AFB的度数；
（2）在图②中，∠AFB的度数为，图③中，∠AFB的度数为；
（3）继续探索，可将本题推广到一般的正n边形情况，用含n的式子表示∠AFB的度数．
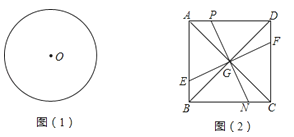
23.问题探究
（1）请在图（1）中作出两条直线，使它们将圆面积四等分，并写出作图过程；
拓展应用
（2）如图（2），M是正方形ABCD内一定点，G是对角线AC、BD的交点．连接GM并延长，分别交AD、BC于P、N．过G做直线EF⊥GM，分别交AB、CD于E、F．求证：PN、EF将正方形ABCD的面积四等分．
