（北师大版）2022-2023学年九年级数学下册3.5确定圆的条件 同步测试
试卷更新日期：2022-10-27 类型：同步测试
一、单选题
-
1. 有一题目：“已知，点 为 的外心， ，求 .”
嘉嘉的解答为：如图，画 以及它的外接圆 ，连接 ， .由 ，得 .
淇淇说：“嘉嘉考虑的不周全， 还应有另一个不同的值.”
下列判断正确的是（ ）
A、淇淇说的对，且 的另一个值是115° B、淇淇说的不对， 就得65° C、嘉嘉求的结果不对， 应得80° D、两人都不对， 应有3个不同的值2. 如图， 是 的外接圆，则点 是 的（ ）．
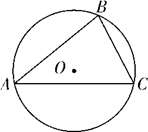A、三条边的垂直平分线的交点 B、三条角平分线的交点 C、三条中线的交点 D、三条高的交点3. 下列说法错误的是（ ）A、等弧所对的圆心角相等 B、弧的度数等于该弧所对的圆心角的度数 C、经过三点可以作一个圆 D、三角形的外心到三角形各顶点距离相等4. 已知⊙O是△ABC的外接圆，若AB＝AC＝5，BC＝6，则⊙O的半径为（ ）A、4 B、3.25 C、3.125 D、2.255. 正三角形的外接圆的半径和高的比为（ ）A、1∶2 B、2∶3 C、3∶4 D、1∶36. 如图，⊙O是△ABC的外接圆，∠AOB=60°，AB=AC=4，则弦BC的长为（ ）
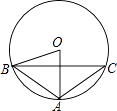A、2 B、4 C、3 D、47. 如图，已知△ABC外接圆的直径为4，∠ABC=120°，那么AC的长度为（ ）
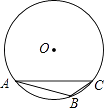A、2 B、2 C、4 D、48. 如图，⊙O的半径为2，△ABC是⊙O的内接三角形，连结OB，OC，若∠BAC与∠BOC互补，则弦BC的长为（ ）
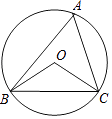A、 B、2 C、2 D、49. 如图，⊙O是△ABC的外接圆，连接OB、OC，若⊙O的半径为2，∠BAC=60°，则BC的长为（ ）
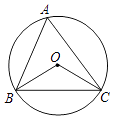A、 B、2 C、4 D、410. 下列命题中，真命题的个数是（ ）①经过三点一定可以作圆；②任意一个圆一定有一个内接三角形，并且只有一个内接三角形；③任意一个三角形一定有一个外接圆，并且只有一个外接圆；④三角形的外心到三角形的三个顶点距离相等．
A、4个 B、3个 C、2个 D、1个二、填空题
-
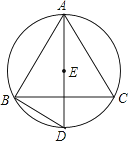
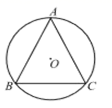
11. 已知△ABC中，点O为△ABC的外心，且∠BOC＝80°，则∠BAC度数为 ．12. 如图，在△ABC中，AB=AC，BC=8．⊙O是△ABC的外接圆，其半径为5．若点A在优弧BC上，则tan∠BAC的值为 ．
13. 如图Rt△ABC中，∠ACB=90°，⊙O是△ABC的外接圆，E为⊙O上一点，连结CE，过C作CD⊥CE，交BE于点D，已知 ，AB= ，DE=5，则tan∠ACE= ．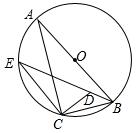
14. 在△ABC中，∠C=90°，AC=5，BC=12，则这个三角形外接圆的半径是 ．15. 如图，网格的小正方形的边长均为1，小正方形的顶点叫做格点．△ABC的三个顶点都在格点上，那么△ ABC的外接圆半径是 ．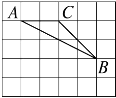
三、解答题
-
16. 如图，已知等腰△ABC，AB＝AC＝8，∠BAC＝120°，请用圆规和直尺作出△ABC的外接圆．并计算此外接圆的半径.
17. 如图，O，H分别是锐角△ABC的外心和垂心，D是BC边上的中点．由H向∠A及其外角平分线作垂线，垂足分别是E，F．求证：D，E，F三点共线．
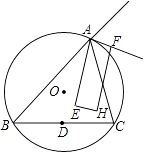18.我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆．例如线段AB的最小覆盖圆就是以线段AB为直径的圆．
（1）请分别作出下图中两个三角形的最小覆盖圆（要求用尺规作图，保留作图痕迹，不写作法）；
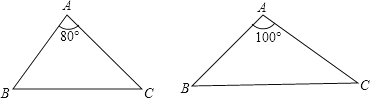
（2）探究三角形的最小覆盖圆有何规律？请写出你所得到的结论（不要求证明）．
19.如图，已知AD既是△ABC的中线，又是角平分线，请判断：
（1）△ABC的形状；
（2）AD是否过△ABC外接圆的圆心O，⊙O是否是△ABC的外接圆，并证明你的结论．
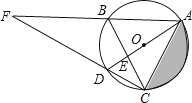
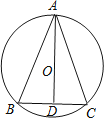20.如图，O是等边△ABC的外心，BO的延长线和⊙O相交于点D，连接DC，DA，OA，OC．
（1）求证：△BOC≌△CDA；
（2）若AB= ， 求阴影部分的面积．
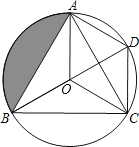21.如图，△ABC是⊙O的内接三角形，AD是⊙O的直径，∠ABC=60°，∠ACB=50°，请解答下列问题：
（1）∠CAD的度数；
（2）设AD、BC相交于E，AB、CD的延长线相交于F，求∠AEC、∠AFC的度数；
（3）若AD=6，求图中阴影部分的面积．
