(北师大版)2022-2023学年九年级数学下册3.2圆的对称性 同步测试
试卷更新日期:2022-10-27 类型:同步测试
一、单选题
-
1. 如图,在⊙O中,若点C是 的中点,∠A=50°,则∠BOC=( )
 A、40° B、45° C、50° D、60°2. 如图,⊙O中,如果∠AOB=2∠COD,那么( )
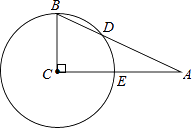
A、40° B、45° C、50° D、60°2. 如图,⊙O中,如果∠AOB=2∠COD,那么( )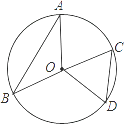 A、AB=DC B、AB<DC C、AB<2DC D、AB>2DC3. 将一个圆分割成三个扇形,它们的圆心角的度数之比为2:3:4,则这个扇形圆心角的度数为( )A、30°,60°,90° B、60°,120°,180° C、50°,100°,150° D、80°,120°,160°4. 将一个圆分成四个扇形,它们的圆心角的度数比为4:4:5:7,则这四个扇形中,圆心角最大的是( )A、54° B、72° C、90° D、126°5. 如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在 上的点D处,折痕交OA于点C,则 的度数为( )
A、AB=DC B、AB<DC C、AB<2DC D、AB>2DC3. 将一个圆分割成三个扇形,它们的圆心角的度数之比为2:3:4,则这个扇形圆心角的度数为( )A、30°,60°,90° B、60°,120°,180° C、50°,100°,150° D、80°,120°,160°4. 将一个圆分成四个扇形,它们的圆心角的度数比为4:4:5:7,则这四个扇形中,圆心角最大的是( )A、54° B、72° C、90° D、126°5. 如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在 上的点D处,折痕交OA于点C,则 的度数为( ) A、40° B、50° C、60° D、70°6. 如图,在三个等圆上各有一条劣弧:弧AB、弧CD、弧EF,如果 + = ,那么AB+CD与EF的大小关系是( )
A、40° B、50° C、60° D、70°6. 如图,在三个等圆上各有一条劣弧:弧AB、弧CD、弧EF,如果 + = ,那么AB+CD与EF的大小关系是( )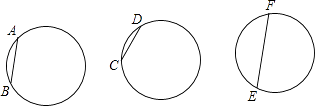 A、AB+CD=EF B、AB+CD<EF C、AB+CD>EF D、大小关系不确定7.
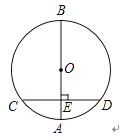
A、AB+CD=EF B、AB+CD<EF C、AB+CD>EF D、大小关系不确定7.如图,已知圆O的直径为6,CD为圆O的直径,且CD⊥AB,∠D=15°.则OE的长为( )
 A、3 B、3 C、 D、8.
A、3 B、3 C、 D、8.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么线段OE的长为( )
 A、6 B、5 C、4 D、39.
A、6 B、5 C、4 D、39.如图,AB是⊙O的直径,⊙O的半径cm,弦CD⊥AB于E,∠CDB=30°,则弦CD的长为( )
 A、cm B、3cm C、2cm D、9cm10. 在半径为1的圆中,长度等于的弦所对的弧的度数为( )A、90° B、145° C、270° D、90°或270°
A、cm B、3cm C、2cm D、9cm10. 在半径为1的圆中,长度等于的弦所对的弧的度数为( )A、90° B、145° C、270° D、90°或270°二、填空题
-
11. 如图,已知BD是⊙O的直径,点A、C在⊙O上, = ,∠AOB=60°,则∠COD的度数是度.
 12. 如图,AB是⊙O的直径,点C在⊙O上,∠AOC=40°,D是BC弧的中点,则∠ACD= .
12. 如图,AB是⊙O的直径,点C在⊙O上,∠AOC=40°,D是BC弧的中点,则∠ACD= . 13. 如图,在⊙O中, = ,若∠AOB=40°,则∠COD=°.
13. 如图,在⊙O中, = ,若∠AOB=40°,则∠COD=°. 14. 在⊙O中,弦AB的长恰好等于半径,弦AB所对的圆心角为 .15. 弦AB将⊙O分成度数之比为1:5的两段弧,则∠AOB=°.
14. 在⊙O中,弦AB的长恰好等于半径,弦AB所对的圆心角为 .15. 弦AB将⊙O分成度数之比为1:5的两段弧,则∠AOB=°.三、解答题
-
16. 如图,AB是⊙O的弦,点C、D在AB上,且AC=BD.判断△OCD的形状,并说明理由.
 17.
17.如图,OA、OB、OC分别是⊙O的半径,且AC=BC,D、E分别是OA、OB的中点,求证:CD=CE.
 18.
18.已知,如图,在⊙O中,AB=DE,BC=EF.求证:AC=DF.
 19.
19.已知如图所示,A,B,C是⊙O上三点,∠AOB=120°,C是
 的中点,试判断四边形OACB形状,并说明理由.
的中点,试判断四边形OACB形状,并说明理由.
四、综合题
-
20. 如图,是一个匀速旋转(指每分钟旋转的弧长或圆心角相同)的摩天轮的示意图,O为圆心,AB为水平地面,假设摩天轮的直径为80米,最低点C离地面为6米,旋转一周所用的时间为6分钟,小明从点C乘坐摩天轮(身高忽略不计),请问:
 (1)、经过2分钟后,小明离开地面的高度大约是多少米?(2)、若小明到了最高点,在视线没有阻挡的情况下能看到周围3公里远的地面景物,则他看到的地面景物有多大面积?(精确到1平方公里)
(1)、经过2分钟后,小明离开地面的高度大约是多少米?(2)、若小明到了最高点,在视线没有阻挡的情况下能看到周围3公里远的地面景物,则他看到的地面景物有多大面积?(精确到1平方公里)