（北师大版）2022-2023学年九年级数学下册3.1圆 同步测试
试卷更新日期：2022-10-27 类型：同步测试
一、单选题
-
1. 下列命题中，正确的是（ ）A、圆只有一条对称轴 B、圆的对称轴不止一条，但只有有限条 C、圆有无数条对称轴，每条直径都是它的对称轴 D、圆有无数条对称轴，经过圆心的每条直线都是它的对称轴2. 在△ABC中，∠C=90°，AB＝3cm，BC＝2cm，以点A为圆心，以2.5cm为半径作圆，则点C和⊙A的位置关系是（ ）
A、C在⊙A上 B、C在⊙A外 C、C在⊙A内 D、C在⊙A位置不能确定。3. 已知矩形ABCD的边AB＝15，BC＝20，以点B为圆心作圆，使A，C，D三点至少有一点在⊙B内，且至少有一点在⊙B外，则⊙B的半径r的取值范围是 （ ）
A、r＞15 B、15＜r＜20 C、15＜r＜25 D、20＜r＜254. 已知⊙O的半径为5cm，点P到圆心O的距离OP=6cm，则点P（ ）A、在⊙O外 B、在⊙O上 C、在⊙O内 D、不能确定5. 如图，在△ABC中，∠ACB=90°，∠A=40°，以C为圆心，CB为半径的圆交AB于点D，连接CD，则∠ACD=（ ）
A、10° B、15° C、20° D、25°6. 已知⊙O的直径为10，点P到点O的距离大于8，那么点P的位置（ ）A、一定在⊙O的内部 B、一定在⊙O的外部 C、一定在⊙O上 D、不能确定7. 如图，四边形PAOB是扇形OMN的内接矩形，顶点P在 上，且不与M、N重合，当P点在 上移动时，矩形PAOB的形状，大小随之变化，则AB的长度（ ）
A、不变 B、变小 C、变大 D、不能确定8. 如图，△ABC中，∠C=90°，AB=5，AC=4，且点D，E分别是AC，AB的中点，若作半径为3的⊙C，则下列选项中的点在⊙C外的是（ ）
A、点B B、点D C、点E D、点A9. 已知⊙O的直径为8cm，点A与O距离为7cm，则点A与⊙O的位置关系是（ ）A、点A在⊙O内 B、点A在⊙O上 C、点A在⊙O外 D、不能确定10. 如图，在6×6的正方形网格中，有6个点，M，N，O，P，Q，R（除R外其余5个点均为格点），以O为圆心，OQ为半径作圆，则在⊙O外的点是（ ）
A、M B、N C、P D、R二、填空题
-
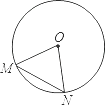
11. 如图，MN为⊙O的弦，∠M=50°，则∠MON等于 ．
12. 已知点O到直线l的距离为6，以O为圆心，r为半径作⊙O，若⊙O上只有3个点到直线l的距离为2，则r的值为 ．13. 已知⊙A的直径是8，点A的坐标是（3，4），那么坐标原点O在⊙A的 ． （填“圆内”、“圆上”或“圆外”）
14. 线段AB=10cm，在以AB为直径的圆上，到点A的距离为5cm的点有个．15. 如图，AB是⊙O的直径，点C在⊙O上，CD⊥AB，垂足为D，已知CD=4，OD=3，求AB的长是 ．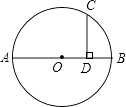
三、解答题
-
16.
如图所示，AB为⊙O的直径，CD是⊙O的弦，AB、CD的延长线交于点E，已知AB=2DE，∠AEC=20°．求∠AOC的度数．
17.如图，有两条公路OM，ON相交成30°，沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学，当拖拉机沿ON方向行驶时，路两旁50米内会受到噪音影响，已知有两台相距30米的拖拉机正沿ON方向行驶，它们的速度均为5米/秒，问这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间是多少？
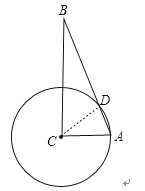
18.如图，BD=OD，∠AOC=114°，求∠AOD的度数．
19.如图，半圆O的直径AB=8，半径OC⊥AB，D为弧AC上一点，DE⊥OC，DF⊥OA，垂足分别为E、F，求EF的长．
20.如图，已知OA、OB是⊙O的两条半径，C、D为OA、OB上的两点，且AC=BD．求证：AD=BC．
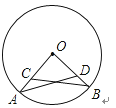21.已知：如图，在△ABC中，∠ACB=90°，∠B=25°，以C为圆心，CA长为半径的圆交AB于D，求
的度数．
