（人教版）2022-2023学年九年级数学下册第29章 投影与视图 同步测试
试卷更新日期：2022-10-27 类型：单元试卷
一、单选题
-
1. 下面属于中心投影的是( )A、太阳光下的树影 B、皮影戏 C、月光下房屋的影子 D、海上日出2. 当棱长为20的正方体的某个面平行于投影面时，这个面的正投影的面积为（ ）A、20 B、300 C、400 D、6003. 小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵随太阳转动的情况，他发现这四个时刻向日葵影子的长度各不相同，那么影子最长的时刻为（ ）
A、上午12时 B、上午10时 C、上午9时30分 D、上午8时4. 一天上午小红先参加了校运动会女子100m比赛，过一段时间又参加了女子400m比赛，如图是摄影师在同一位置拍摄的两张照片，那么下列说法正确的是（ ）
A、乙照片是参加100 m的 B、甲照片是参加400 m的 C、乙照片是参加400 m的 D、无法判断甲、乙两张照片5. 如图所示的几何体的主视图是（ ）
A、
B、
C、
D、
6. 如图所示的几何体的俯视图是（ ）
A、
B、
C、
D、
7. 如图是某几何体的三视图，这个几何体可以是（ ）
A、
B、
C、
D、
8. 某正方体的每个面上都有一个汉字，它的一个展开图如图说是，正原正方体中，与“考”字所在面相对的面上的汉字是（ ）
A、祝 B、你 C、成 D、功9. 一个几何体的展开图如图所示，这个几何体是（ ）
A、三棱柱 B、三棱锥 C、四棱柱 D、四棱锥10.如图，是正方体包装盒的平面展开图，如果在其中的三个正方形A、B、C内分别填上适当的数，使得将这个平面展开图折成正方体后，相对面上的两数字互为相反数，则填在A、B、C内的三个数字依次为（ ）
A、0，1，﹣2 B、1，0，﹣2 C、﹣2，0，1 D、0，﹣2，1二、填空题
-
11. 小明的身高是
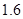米，他的影长是 
米，同一时刻古塔的影长是 
米，则古塔的高是米．
12. 如图，林林在A时测得某树的影长为2 m，B时又测得该树的影长为8 m，若两次日照的光线互相垂直，则该树的高度为
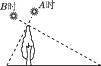13. 某几何体的三视图如图所示，则其表面积为.
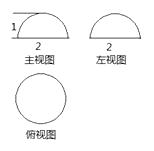14. 长方体的主视图和左视图如图所示(单位：cm)，则其俯视图的面积是 。
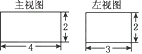15.如图，若要使图中平面展开图折叠成正方体后，相对面上两个数字之和为6，则x﹣y= ．
三、解答题
-
16.
（1）如图①所示，AB和DE是直立在地面上的两根木杆，BC是AB在太阳光下的影子，请你在图中画出此时木杆DE的影子（用线段EF表示）．
图②是直立在地面上的两根木杆及它们在灯光下的影子，请你在图中画出光源的位置（用点O表示）；
（2）太阳光线与地面成60°的角，照射在地面上的一只皮球上，皮球在地面上的投影长是20cm，请你求出皮球的半径．
17.在生活中需测量一些球的足球、篮球）的直径．某校研究性学习小组，通过实验发现下面的测量方法：如图，将球放在水平的桌面上，在阳光的斜射下，得到球的影子AB，设光线DA、CB分别与球相切于点E、F，则EF即为球的直径．若测得AB的长为41.5cm，∠ABC=37°．请你计算出球的直径（精确到1cm）．
18.如图分别是两根木棒及其影子的情形．
（1）哪个图反映了太阳光下的情形？哪个图反映了路灯下的情形？
（2）在太阳光下，已知小明的身高是1.8米，影长是1.2米，旗杆的影长是4米，求旗杆的高；
（3）请在图中分别画出表示第三根木棒的影长的线段．
19.如图为一机器零件的三视图．
（1）请写出符合这个机器零件形状的几何体的名称；
（2）若俯视图中三角形为正三角形，那么请根据图中所标的尺寸，计算这个几何体的表面积（单位：cm2）
20.如图，是由几个相同的小立方块搭成的几何体从正面、左面看到的图形，问这个几何体有几个小立方块？
21.用小立方块搭成的几何体，主视图和俯视图如图，问这样的几何体有多少可能？它最多需要多少小立方块，最少需要多少小立方块．
