(人教版)2022-2023学年九年级数学下册28章锐角三角函数 同步测试
试卷更新日期:2022-10-27 类型:单元试卷
一、单选题
-
1. 如图1,是数学家毕达哥拉斯根据勾股定理所画的“勾股树”.如图2,在Rt△ABC中, , 以其三边为边分别向外作正方形,延长EC,DB分别交GF,AH于点N,K,连接KN交AG于点M,若 , 则为( )
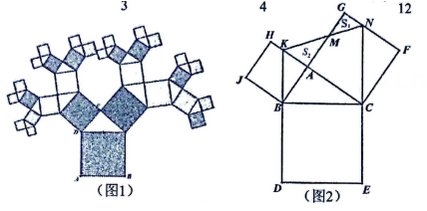 A、 B、 C、 D、2. 在Rt△ABC中,∠C=90°,各边都扩大5倍,则tanA的值( )A、不变 B、扩大5倍 C、缩小5倍 D、不能确定3. 如图:四个形状大小相同的等腰三角形△ABE,△ADF,△CDG,△BCH按如图摆放在正方形ABCD的内部,顺次连接E、F、G、H得到四边形EFGH.若∠AEB=∠AFD=∠CGD=∠BHC=120°,且EH= ﹣ ,则BC的长为( )
A、 B、 C、 D、2. 在Rt△ABC中,∠C=90°,各边都扩大5倍,则tanA的值( )A、不变 B、扩大5倍 C、缩小5倍 D、不能确定3. 如图:四个形状大小相同的等腰三角形△ABE,△ADF,△CDG,△BCH按如图摆放在正方形ABCD的内部,顺次连接E、F、G、H得到四边形EFGH.若∠AEB=∠AFD=∠CGD=∠BHC=120°,且EH= ﹣ ,则BC的长为( ) A、 B、4 ﹣4 C、2 D、24. 如图,在△ABC中,sinB= , tanC=2,AB=3,则AC的长为( )
A、 B、4 ﹣4 C、2 D、24. 如图,在△ABC中,sinB= , tanC=2,AB=3,则AC的长为( ) A、 B、 C、 D、25. 计算2sin60°的值为( )A、 B、 C、1 D、6. 如图,在中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )
A、 B、 C、 D、25. 计算2sin60°的值为( )A、 B、 C、1 D、6. 如图,在中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( ) A、c=bsinB B、b=csinB C、a=btanB D、b=ctanB7. 如图,点A,B,C在正方形网格的格点上,则sin∠BAC=( )
A、c=bsinB B、b=csinB C、a=btanB D、b=ctanB7. 如图,点A,B,C在正方形网格的格点上,则sin∠BAC=( )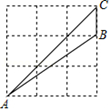 A、 B、 C、 D、8. 如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为120m,则这栋楼的高度为( )
A、 B、 C、 D、8. 如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为120m,则这栋楼的高度为( ) A、160m B、120m C、300m D、160m9. 重庆移动为了提升新型冠状肺炎“停课不停学”期间某片区网络信号,保证广大师生网络授课、听课的质量,临时在坡度为i=1:2.4的山坡上加装了信号塔PQ(如图所示),信号塔底端Q到坡底A的距离为3.9米.同时为了提醒市民,在距离斜坡底A点4.4米的水平地面上立了一块警示牌MN.当太阳光线与水平线成53°角时,测得信号塔PQ落在警示牌上的影子EN长为3米,则信号塔PQ的高约为( )
A、160m B、120m C、300m D、160m9. 重庆移动为了提升新型冠状肺炎“停课不停学”期间某片区网络信号,保证广大师生网络授课、听课的质量,临时在坡度为i=1:2.4的山坡上加装了信号塔PQ(如图所示),信号塔底端Q到坡底A的距离为3.9米.同时为了提醒市民,在距离斜坡底A点4.4米的水平地面上立了一块警示牌MN.当太阳光线与水平线成53°角时,测得信号塔PQ落在警示牌上的影子EN长为3米,则信号塔PQ的高约为( )(结果精确到十分位, 参考数据:sin 53°≈0.8, cos 53°≈0.6, tan 53°≈1.3)
 A、10.4 B、11.9 C、11.4 D、13.410. 如图,BD是菱形ABCD的对角线,CE⊥AB于点E,且点E是AB的中点,则tan∠BFE的值是( )
A、10.4 B、11.9 C、11.4 D、13.410. 如图,BD是菱形ABCD的对角线,CE⊥AB于点E,且点E是AB的中点,则tan∠BFE的值是( )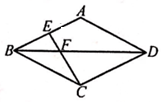 A、 B、 C、2 D、
A、 B、 C、2 D、二、填空题
-
11. 若 为锐角,且 ,则 °.12. 关于x的一元二次方程 +tanα=0有两个相等的实数根,则锐角α = .13. 如图,在△ABC中,AB=AC=5, ,将△ABC绕点B逆时针旋转,得到 ,当点 在线段CA延长线上时 的面积为 .
 14. 如图,菱形 的边长为15, ,则 .
14. 如图,菱形 的边长为15, ,则 . 15. 如图,航拍无人机从A处测得一幢建筑物顶部 的仰角为 ,测得底部C的俯角为 ,此时航拍无人机与该建筑物的水平距离AD为120m,那么该建筑物的高度BC约为m(结果保留整数, ).
15. 如图,航拍无人机从A处测得一幢建筑物顶部 的仰角为 ,测得底部C的俯角为 ,此时航拍无人机与该建筑物的水平距离AD为120m,那么该建筑物的高度BC约为m(结果保留整数, ).
三、解答题
-
16. 先化简,再求代数式 的值,其中m=2cos30°-tan45°17. 已知α为锐角,且tanα是方程x2+2x﹣3=0的一个根,求2sin2α+cos2α﹣tan(α+15°)的值.18. 已知△ABC中的∠A与∠B满足(1﹣tanA)2+|sinB﹣|=0
(1)试判断△ABC的形状.
(2)求(1+sinA)2﹣2﹣(3+tanC)0的值.
19. (1)如图1,4条直线l1、l2、l3、l4是一组平行线,相邻2条平行线的距离都是2cm,正方形ABCD的4个顶点A、B、C、D分别在l1、l3、l4、l2上,求该正方形的面积;(2)如图2,把一张矩形卡片ABCD放在每格宽度为18mm的横格纸中,恰好四个顶点都在横格线上,已知∠1=36°,求长方形卡片的周长.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
 20. 如图所示,图1,图2分别是某款高压电塔的实物图和示意图电塔的底座AB与地面平齐,DF表示电塔顶端D到地面的距离,已知AF的长是2米,支架AC与地面夹角∠BAC=86°,顶端支架DC长10米,DC与水平线CE之间夹角∠DCE=45°,求电塔的高度DF.(sin86°=0.998,cos86°=0.070,tan86°=14.300, ≈1.4,结果保留整数)
20. 如图所示,图1,图2分别是某款高压电塔的实物图和示意图电塔的底座AB与地面平齐,DF表示电塔顶端D到地面的距离,已知AF的长是2米,支架AC与地面夹角∠BAC=86°,顶端支架DC长10米,DC与水平线CE之间夹角∠DCE=45°,求电塔的高度DF.(sin86°=0.998,cos86°=0.070,tan86°=14.300, ≈1.4,结果保留整数) 21. 如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四
21. 如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知0=36°,求AB和AD的长. (结果精确到1mm,参考数据: , , )


