(人教版)2022-2023学年九年级数学下册28.2解直角三角形及其应用 同步测试
试卷更新日期:2022-10-27 类型:同步测试
一、单选题
-
1. 如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为a,则两梯脚之间的距离BC为( )
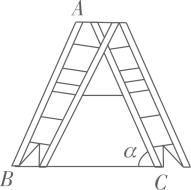 A、4cos a B、4sin a C、4tan a D、2. 如图所示,从一热气球的探测器A点,看一栋高楼顶部B点的仰角为30°,看这栋高楼底部C点的俯角为60°,若热气球与高楼的水平距离为30m,则这栋高楼高度是( )
A、4cos a B、4sin a C、4tan a D、2. 如图所示,从一热气球的探测器A点,看一栋高楼顶部B点的仰角为30°,看这栋高楼底部C点的俯角为60°,若热气球与高楼的水平距离为30m,则这栋高楼高度是( ) A、60m B、40 m C、30 m D、60 m3. 如图在某山坡前有一电视塔,小明在山坡坡脚P处测得电视塔顶端M的仰角为60°,在点P处小明沿山坡向上走 到达D处,测得电视塔顶端M的仰角为30°,已知山坡坡度 ,请你计算电视塔的高度 约为( )(结果精确到 ,参考数据: )
A、60m B、40 m C、30 m D、60 m3. 如图在某山坡前有一电视塔,小明在山坡坡脚P处测得电视塔顶端M的仰角为60°,在点P处小明沿山坡向上走 到达D处,测得电视塔顶端M的仰角为30°,已知山坡坡度 ,请你计算电视塔的高度 约为( )(结果精确到 ,参考数据: ) A、59.8 B、58.8 C、53.7 D、57.94. 如图,在正方形 中,对角线 相交于点 ,以 为边向外作等边 ,连接 交 于 若点 为 的延长线上一点,连接 ,连接 且 平分 ,下列选项正确的有( )
A、59.8 B、58.8 C、53.7 D、57.94. 如图,在正方形 中,对角线 相交于点 ,以 为边向外作等边 ,连接 交 于 若点 为 的延长线上一点,连接 ,连接 且 平分 ,下列选项正确的有( )① ;② ;③ ;④
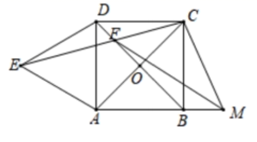 A、 个 B、 个 C、 个 D、 个5. 如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离 为 ,那么该建筑物的高度 约为( )
A、 个 B、 个 C、 个 D、 个5. 如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离 为 ,那么该建筑物的高度 约为( ) A、 B、 C、 D、6. 如图,一架无人机航拍过程中在 处测得地面上 , 两个目标点的俯角分别为 和 .若 , 两个目标点之间的距离是100米,则此时无人机与目标点 之间的距离(即 的长)为( )
A、 B、 C、 D、6. 如图,一架无人机航拍过程中在 处测得地面上 , 两个目标点的俯角分别为 和 .若 , 两个目标点之间的距离是100米,则此时无人机与目标点 之间的距离(即 的长)为( )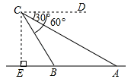 A、100米 B、 米 C、50米 D、 米7. 如图,在圆O中,直径AB平分弦CD于点E,且CD= ,连接AC,OD,若∠A与∠DOB互余,则EB的长是( )
A、100米 B、 米 C、50米 D、 米7. 如图,在圆O中,直径AB平分弦CD于点E,且CD= ,连接AC,OD,若∠A与∠DOB互余,则EB的长是( ) A、 B、4 C、 D、28. 如图,在菱形ABCD中,DE⊥AB, ,AE=3,则tan∠DBE的值是( )
A、 B、4 C、 D、28. 如图,在菱形ABCD中,DE⊥AB, ,AE=3,则tan∠DBE的值是( )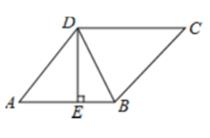 A、 B、2 C、 D、9. 如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE·OP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE= ,其中正确结论的个数是( )
A、 B、2 C、 D、9. 如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE·OP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE= ,其中正确结论的个数是( ) A、1 B、2 C、3 D、410. 图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A、1 B、2 C、3 D、410. 图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )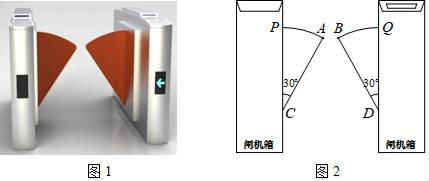 A、(54 +10) cm B、(54 +10) cm C、64 cm D、54cm
A、(54 +10) cm B、(54 +10) cm C、64 cm D、54cm二、填空题
-
11. 如图,在一笔直的海岸线l上有A、B两个观测站,AB=6 km.从A站测得船C在北偏东45°的方向,从B站测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为km.
 12. 如图,已知直线 , 与 之间的距离为2,在 中, ,点 是直线 上的一个动点, , 中有一边是 的 倍,将 绕点 顺时针旋转 得到 , 所在直线交 于点 ,则 的长度为 .
12. 如图,已知直线 , 与 之间的距离为2,在 中, ,点 是直线 上的一个动点, , 中有一边是 的 倍,将 绕点 顺时针旋转 得到 , 所在直线交 于点 ,则 的长度为 .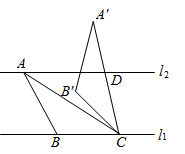 13. 如图,在⊙O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD的中点,则AC的长是.
13. 如图,在⊙O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD的中点,则AC的长是. 14. 如图,C,D是两个村庄,分别位于一个湖的南,北两端A和B的正东方向上,且点D位于点C的北偏东60°方向上,CD=12km,则AB=km.
14. 如图,C,D是两个村庄,分别位于一个湖的南,北两端A和B的正东方向上,且点D位于点C的北偏东60°方向上,CD=12km,则AB=km. 15. 如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西方向行驶千米至B地,再沿北偏东方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,则B,C两地的距离千米.
15. 如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西方向行驶千米至B地,再沿北偏东方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,则B,C两地的距离千米.
三、解答题
-
16. 如图是某地摩天轮(图1)和示意图(图2),已知线段 经过圆心 且垂直于地面,垂足为点 ,当座舱在点 时,测得摩天轮顶端点 的仰角为 ,同时测得点 的俯角为 ,又知摩天轮的半径为 米,求摩天轮顶端 与地面的距离.(精确到 米)
参考数据: ,
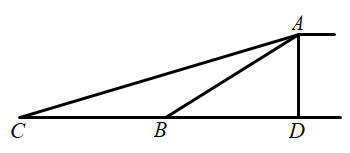
 17. 如图,某教学兴趣小组想测量某建筑物的高度,他们在A点测得屋顶C的仰角为30°,然后沿AD方向前进10米,到达B点,在B点测得屋顶C的仰角为60°,已知测量仪AE的高度为1米,请你根据他们的测量数据计算建筑物CF的高度(结果保留根号).
17. 如图,某教学兴趣小组想测量某建筑物的高度,他们在A点测得屋顶C的仰角为30°,然后沿AD方向前进10米,到达B点,在B点测得屋顶C的仰角为60°,已知测量仪AE的高度为1米,请你根据他们的测量数据计算建筑物CF的高度(结果保留根号). 18. 市政府为了方便市民绿色出行,推出了共享单车服务.图1是某品牌共享单车放在水平地面上的实物图,图2是其示意图,其中 都与地面 平行, 坐垫 与点 的距离 为 .根据经验,当坐垫 到 的距离调整为人体腿长的 时,坐骑比较舒适.小明的腿长约为 ,现将坐垫 调整至坐骑舒适高度位置 ,求 的长,(结果精确到 ,参考数据: )
18. 市政府为了方便市民绿色出行,推出了共享单车服务.图1是某品牌共享单车放在水平地面上的实物图,图2是其示意图,其中 都与地面 平行, 坐垫 与点 的距离 为 .根据经验,当坐垫 到 的距离调整为人体腿长的 时,坐骑比较舒适.小明的腿长约为 ,现将坐垫 调整至坐骑舒适高度位置 ,求 的长,(结果精确到 ,参考数据: )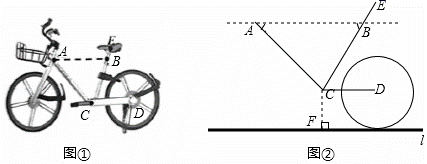 19. 如图,某校有一教学楼 ,其上有一避雷针 为 米,教学楼后面有一小山,其坡度为 山坡上有一休息亭 供爬山人员休息,测得山坡脚 与教学搂的水平距离 为 米,与休息亭的距离 为 米,从休息亭 测得教学楼上避雷针顶点 的仰角为 ,求教学搂 的高度.(结果保留根号)(注:坡度 是指坡面的铅直高度与水平宽度的比)
19. 如图,某校有一教学楼 ,其上有一避雷针 为 米,教学楼后面有一小山,其坡度为 山坡上有一休息亭 供爬山人员休息,测得山坡脚 与教学搂的水平距离 为 米,与休息亭的距离 为 米,从休息亭 测得教学楼上避雷针顶点 的仰角为 ,求教学搂 的高度.(结果保留根号)(注:坡度 是指坡面的铅直高度与水平宽度的比) 20. 如图,大楼 高 ,附近有一座塔 ,某人在楼底A处测得塔顶的仰角为 ,爬到楼顶D处测得塔顶的仰角为 分别求塔高 及大楼与塔之间的距离 的长.(结果精确到 ,参考数据: , , , ,)
20. 如图,大楼 高 ,附近有一座塔 ,某人在楼底A处测得塔顶的仰角为 ,爬到楼顶D处测得塔顶的仰角为 分别求塔高 及大楼与塔之间的距离 的长.(结果精确到 ,参考数据: , , , ,)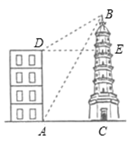 21. 某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,如图所示,已知原阶梯式自动扶梯 长为 ,坡角 为 ”改造后的斜坡式自动扶梯的坡角 为 ,若国标规定自动扶梯的速度一般是 ,请你计算乘坐改造后的斜坡式自动扶梯比乘坐阶梯式自动扶梯多用的时间.(结果保留整数,参考数据: , , .)
21. 某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,如图所示,已知原阶梯式自动扶梯 长为 ,坡角 为 ”改造后的斜坡式自动扶梯的坡角 为 ,若国标规定自动扶梯的速度一般是 ,请你计算乘坐改造后的斜坡式自动扶梯比乘坐阶梯式自动扶梯多用的时间.(结果保留整数,参考数据: , , .)