(人教版)2022-2023学年九年级数学下册28.1 锐角三角函数 同步测试
试卷更新日期:2022-10-27 类型:同步测试
一、单选题
-
1. 如图,AB是⊙O的直径,AB=4,AC是弦,AC=2 ,∠AOC=( )
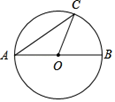 A、120° B、130° C、140° D、150°2. 已知正三角形外接圆半径为 , 这个正三角形的边长是( )A、 B、 C、 D、3. 在Rt△ABC中,∠C=90°,BC=8,AB=10,则sinA的值为( )A、 B、 C、 D、以上都不对4. 如图, 已知第一象限内的点A在反比例函数y= 的图象上, 第二象限内的点B在反比例函数y= 的图象上, 且OA⊥OB, cosA= , 则k的值为( )
A、120° B、130° C、140° D、150°2. 已知正三角形外接圆半径为 , 这个正三角形的边长是( )A、 B、 C、 D、3. 在Rt△ABC中,∠C=90°,BC=8,AB=10,则sinA的值为( )A、 B、 C、 D、以上都不对4. 如图, 已知第一象限内的点A在反比例函数y= 的图象上, 第二象限内的点B在反比例函数y= 的图象上, 且OA⊥OB, cosA= , 则k的值为( )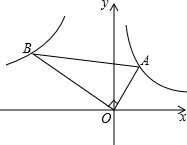 A、-12 B、-16 C、-6 D、-185. 如图,已知AD是等腰三角形ABC底边上的高,且sinB= ,点E在AC上且AE:EC=2:3,则tan∠ADE=( )
A、-12 B、-16 C、-6 D、-185. 如图,已知AD是等腰三角形ABC底边上的高,且sinB= ,点E在AC上且AE:EC=2:3,则tan∠ADE=( ) A、 B、 C、 D、6. 如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则sin∠ECF=( )
A、 B、 C、 D、6. 如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则sin∠ECF=( ) A、 B、 C、 D、7. 如图,已知A,B两点的坐标分别为(8,0),(0,8),点C,F分别是直线x=﹣5和x轴上的动点,CF=10,点D是线段CF的中点,连接AD交y轴于点E,当△ABE面积取得最小值时,sin∠BAD的值是( )
A、 B、 C、 D、7. 如图,已知A,B两点的坐标分别为(8,0),(0,8),点C,F分别是直线x=﹣5和x轴上的动点,CF=10,点D是线段CF的中点,连接AD交y轴于点E,当△ABE面积取得最小值时,sin∠BAD的值是( )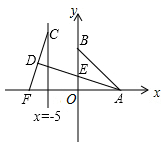 A、 B、 C、 D、8. 2tan30°的值等于( )A、 B、 C、 D、9. 如图,已知扇形OAB的半径为r,C是弧AB上的任一点(不与A,B重合),CM⊥OA,垂足为M,CN⊥OB,垂足为N,连接MN,若∠AOB= ,则MN可用 表示为( )
A、 B、 C、 D、8. 2tan30°的值等于( )A、 B、 C、 D、9. 如图,已知扇形OAB的半径为r,C是弧AB上的任一点(不与A,B重合),CM⊥OA,垂足为M,CN⊥OB,垂足为N,连接MN,若∠AOB= ,则MN可用 表示为( )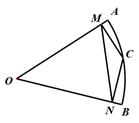 A、 B、 C、 D、10. 在 中, , , ,则 的值为( )A、 B、 C、 D、
A、 B、 C、 D、10. 在 中, , , ,则 的值为( )A、 B、 C、 D、二、填空题
-
11. 已知是锐角 , 则.12. 如图,在4×4的正方形网格中,△ABC的顶点都在边长为1的小正方形的顶点上,则tan∠ACB的值为 .
 13. 计算: .14. 在△ABC中,∠C=90°,若AB=3,BC=1,则cosA的值为 .15. 如图, 和 均是等边三角形,其中点 是 的内心,以 为圆心, 长为半径画弧交 于点 ,再将弧 绕点 逆时针旋转60°至弧 处,已知 ,则图中阴影部分面积是 .
13. 计算: .14. 在△ABC中,∠C=90°,若AB=3,BC=1,则cosA的值为 .15. 如图, 和 均是等边三角形,其中点 是 的内心,以 为圆心, 长为半径画弧交 于点 ,再将弧 绕点 逆时针旋转60°至弧 处,已知 ,则图中阴影部分面积是 .
三、解答题
-
16. 先化简,再求代数式的值,其中17. 如果等腰三角形两腰上的高之和等于底边上的高,请猜测这个三角形底角的正切值.18. 在Rt△ABC中,AC=4,BC=3,求sinA的值.
19. 如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,sinα= ,求t的值. 20. 如图,在正方形ABCD中,M是AD的中点,BE=3AE,试求sin∠ECM的值.
20. 如图,在正方形ABCD中,M是AD的中点,BE=3AE,试求sin∠ECM的值.

