鲁教版（五四学制）2022-2023学年九年级数学下册6.3用频率估计概率同步测试
试卷更新日期：2022-10-26 类型：同步测试
一、单选题
-
1. 在一个不透明的布袋中装有红色.白色玻璃球共40个，除颜色外其他完全相同，小明通过多次摸球试验后发现，其中摸到白色球的频率稳定在85％左右，则口袋中红色球可能有（ ）.A、34个 B、30个 C、10个 D、6个2. 下列说法正确的是（ ）A、某彩票的中奖概率是5%，那么买100张彩票一定有5张中奖 B、某次试验投掷次数是500，计算机记录“钉尖向上”的次数是308，则该次试验“钉尖向上”的频率是0.616 C、当试验次数很大时，概率稳定在频率附近 D、试验得到的频率与概率不可能相等3. 某人做投硬币试验时，投掷 次，正面朝上 次（即正面朝上的频率 ），则下列说法正确的是（ ）A、 一定等于 B、 一定不等于 C、多投一次， 更接近 D、投掷次数逐渐增加， 稳定在 附近4. 某收费站在2小时内对经过该站的机动车统计如下：
类型
轿车
货车
客车
其他
数量（辆）
36
24
8
12
若有一辆机动车将经过这个收费站，利用上面的统计估计它是轿车的概率为（ ）
A、 B、 C、 D、5. 下列说法正确的是（ ）A、连续抛一枚硬币n次，当n越来越大时，出现正面朝上的频率会越来越稳定于0.5 B、连续抛一枚硬币50次，出现正面朝上的次数是25次 C、连续三次掷一颗骰子都出现了奇数，则第四次出现的数一定是偶数 D、某地发行一种福利彩票，中奖概率为1%，买这种彩票100张一定会中奖6. 盒子中有白色乒乓球8个和黄色乒乓球若干个，为求得盒中黄色乒乓球的个数，某同学进行了如下实验：每次摸出一个乒乓球记下它的颜色，如此重复360次，摸出白色乒乓球90次，则黄色乒乓球的个数估计为（ ）A、90个 B、24个 C、70个 D、32个7. 某市大约有100万人口，随机抽查了2000人，具有大专以上学历的有120人，则在该市随便调查一个人，他具有大专以上学历的概率为（ ）A、6％ B、12％ C、20％ D、以上都不正确8. 在一个不透明的口袋中装有4个红球和若干个白球，他们除颜色外其他完全相同．通过多次摸球实验后发现，摸到红球的频率稳定在25%附近，则口袋中白球可能有（ ）A、12个 B、14个 C、15个 D、16个9. 一个不透明的布袋中装着只有颜色不同的红、黄两种小球，其中红色小球有8个，为估计袋中黄色小球的数目，每次将袋中小球搅匀后摸出一个小球记下颜色，然后放回袋中，再次搅匀……多次试验发现摸到红球的频率是 ， 则估计黄色小球的数目是（ ）A、2个 B、20个 C、40个 D、48个10. 在一个不透明的布袋中，红球、黑球、白球共有若干个，除颜色外，形状、大小、质地等完全相同．小新从布袋中随机摸出一球，记下颜色后放回布袋中，摇匀后再随机摸出一球，记下颜色，……，如此大量摸球实验后，小新发现从中摸出红球的频率稳定于20%，摸出黑球的频率稳定于50%．对此实验，他总结出下列结论：①若进行大量摸球实验，摸出白球的频率应稳定于30%；②若从布袋中任意摸出一个球，该球是黑球的概率最大；③若再摸球100次，必有20次摸出的球是红球．其中说法正确的是（ ）
A、①②③ B、①② C、①③ D、②③二、填空题
-
11. 某篮球运动员进行定点投篮训练，其成绩如下表：
投篮次数
10
100
10000
投中次数
9
89
9012
则这名运动员定点投篮一次，投中的概率约是(精确到0.1)
12. 在一个不透明的布袋中，装有红、黑、白三种只有颜色不同的小球，其中红色小球4个，黑、白色小球的数目相同.小明从布袋中随机摸出一球，记下颜色后放回布袋中，摇匀后随机摸出一球，记下颜色；…如此大量摸球实验后，小明发现其中摸出的红球的频率稳定于20%，由此可以估计布袋中的黑色小球有个.13. 某市对一批口罩进行抽检，统计合格口罩的只数，得到口罩的合格频率如下：抽检只数（只）
50
100
150
500
1 000
2 000
10 000
50 000
合格频率
0.82
0.83
0.82
0.83
0.84
0.84
0.84
0.84
则从该批口罩中任抽一只口罩，是合格品的概率约为.
14. 2020年3月12日是我国第42个植树节，某林业部门要考察种幼树在一定条件下的移植成活率，幼树移植过程中的一组统计数据如下表：幼树移植数（棵）
100
2500
4000
8000
20000
30000
幼树移植成活数（棵）
87
2215
3520
7056
17580
26430
幼树移植成活的频率
0.870
0.886
0.880
0.882
0.879
0.881
请根据统计数据，估计这种幼树在此条件下移植成活的概率是 ． （结果精确到0.01）
15. 一口袋中有6个红球和若干个白球，除颜色外均相同，从口袋中随机摸出一球，记下颜色，再把它放回口袋中摇匀．重复上述实验共300次，其中120次摸到红球，则口袋中大约有个白球．
三、解答题
-
16. 对某厂生产的直径为4cm的乒乓球进行产品质量检查，结果如下：(1)、计算各次检查中“优等品”的频率，填入表中；
抽取球数n 50 100 500 1000 5000 优等品数m 45 92 455 890 4500 优等品频率 (2)、该厂生产乒乓球优等品的概率约为多少?17. 一个口袋中有5个黑球和若干个白球，从口袋中随机摸出一球，记下其颜色，再把它放回摇均，重复上述过程，共实验100次，其中75次摸到白球，于是可以估计袋中共有多少球？18. 小颖和小红两位同学在做投掷骰子（质地均匀的正方体）实验，他们共做了60次实验，实验的结果如下：朝上的点数
1
2
3
4
5
6
出现的次数
7
9
6
8
20
10
（1）计算“3点朝上”的频率和“5点朝上”的频率．
（2）小颖说：“根据实验得出，出现5点朝上的机会最大”；小红说：“如果投掷600次，那么出现6点朝上的次数正好是100次．”小颖和小红的说法正确吗？为什么？
19. 目前我市“校园手机”现象越来越受到社会关注，针对这种现象，我市某中学九年级数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的看法，统计整理并制作了如下的统计图：
(1)、这次调查的家长总数为人．家长表示“不赞同”的人数为人；(2)、请在图①中把条形统计图补充完整；
(3)、从这次接受调查的家长中随机抽查一个，恰好是“赞同”的家长的概率是；
(4)、求图②中表示家长“无所谓”的扇形圆心角的度数．20. 在一个暗箱里放有a个除颜色外都完全相同的红、白、蓝三种球，其中红球有4个，白球有10个，每次将球搅拌均匀后，任意摸出一个球记下颜色再放回暗箱．通过大量重复摸球实验后发现，摸到红球的频率稳定在20%．（1）试求出a的值；
（2）从中任意摸出一个球，下列事件：①该球是红球；②该球是白球；③该球是蓝球．试估计这三个事件发生的可能性的大小，并将三个事件按发生的可能性从小到大的顺序排列（用序号表示事件）．
21. 甲、乙两位同学做抛骰子（均匀正方体形状）实验，他们共抛了60次，出现向上点数的次数如表：向上点数
1
2
3
4
5
6
出现次数
8
10
7
9
16
10
（1）计算出现向上点数为6的频率．
（2）丙说：“如果抛600次，那么出现向上点数为6的次数一定是100次．”请判断丙的说法是否正确并说明理由．
（3）如果甲乙两同学各抛一枚骰子，求出现向上点数之和为3的倍数的概率．
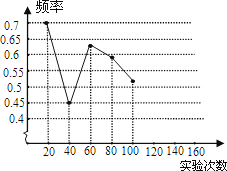
22.一粒木质中国象棋棋子“車”，它的正面雕刻一个“車”字，它的反面是平的，将棋子从一定高度下抛，落地反弹后可能是“車”字面朝上，也可能是“車”字朝下．由于棋子的两面不均匀，为了估计“車”字朝上的机会，某实验小组做了棋子下抛实验，并把实验数据整理如下：
实验次数
20
40
60
80
100
120
140
160
“車”字朝上的频数
14
18
38
47
52
78
88
相应的频率
0.7
0.45
0.63
0.59
0.52
0.55
0.56
（1）请将表中数据补充完整，并画出折线统计图中剩余部分．
（2）如果实验继续进行下去，根据上表数据，这个实验的频率将接近于该事件发生的机会，请估计这个机会约是多少？
（3）在（2）的基础上，进一步估计：将该“車”字棋子，按照实验要求连续抛2次，则刚好使“車”字一次字面朝上，一次朝下的可能性为多少？
23. 六一期间，某公园游戏场举行“迎奥运”活动．有一种游戏的规则是：在一个装有6个红球和若干个白球（每个球除颜色外其他相同）的袋中，随机摸一个球，摸到一个红球就得到一个奥运福娃玩具．已知参加这种游戏活动为40000人次，公园游戏场发放的福娃玩具为10000个．（1）求参加一次这种游戏活动得到福娃玩具的概率；
（2）请你估计袋中白球接近多少个？