鲁教版（五四学制）2022-2023学年九年级数学下册6.2生活中的概率同步测试
试卷更新日期：2022-10-26 类型：同步测试
一、单选题
-
1. “比赛中，郭艾伦罚篮命中”，这一事件是（ ）A、必然事件 B、不可能事件 C、随机事件 D、确定事件2. 如图，有一些写有号码的卡片，它们的背面都相同，现将它们背面朝上，从中任意摸出一张，摸到 号卡片的概率是（ ）
A、 B、 C、 D、3. 一只小虫子欲从A点不重复经过图中的点或者线段，而最终到达目的地E，这只小虫子的不同走法共有（ ）
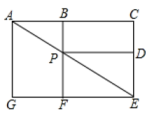A、12种 B、13种 C、14种 D、15种4. 端午节那天，欢欢回家看到桌上有一盆粽子，其中豆沙馅粽子1个，板栗馅粽子2个，五花肉馅粽子1个，这些粽子除馅外无其它差别.欢欢从盆中随机取出1个粽子，是豆沙馅粽子的概率是（ ）A、 B、 C、 D、5. 一个不透明的盒子中装有2个黑球和4个白球，这些球除颜色外其他均相同，从中任意摸出3个球，下列事件为必然事件的是（ ）A、至少有1个黑球 B、至少有2个黑球 C、至少有1个白球 D、至少有2个白球6. 在下列事件中，必然事件是（ ）A、购买一张体育彩票，中奖 B、随意翻到一本书的某页，这页的页码是奇数 C、射击运动员射击一次，命中靶心 D、任意画一个圆的内接四边形，其对角互补7. 不透明袋子中有除颜色外完全相同的2个黑球和4个白球，从袋中随机摸出3个球，下列事件是必然事件的是（ ）A、2个白球1个黑球 B、至少有1个白球 C、3个都是白球 D、2个黑球1个白球8. 如图，在的正方形网格中有9个格点，已经取定点A和B，在余下的7个点中任取一点C，使为直角三角形的概率是（ ）
A、 B、 C、 D、9. 如图，有4张形状大小质地均相同的卡片，正面印有速度滑雪．雪橇、冰壶、冬季两项等四种不同的图案，背面完全相同：
现将这4张卡片洗匀后正面向下放在桌子上，从中随机抽取一张，抽出的卡片正面恰好是冰壶项目图案的概率是（ ）
A、 B、 C、 D、10. 下列事件中：①明天会下雨；②一个班（40人）里有两人的生日在同一天；③从装着红球和黑球的袋子里摸出白球；④太阳东升西落.
不可能事件的个数为（ ）
A、1 B、2 C、3 D、4二、填空题
-
11. 从长度分别为2cm，3cm，5cm，6cm的四根木棍中随机取三根，能构成三角形的概率是 ．12. 天一和润泽两位小朋友做游戏，在一个不透明的袋子中有4个分别标有数字6，2， ， 的球，这些球除所标的数字不同外其他都相同，从袋子中随机摸出两个球，若这两个球上的两个数字之积为负数则天一赢，若这两个球上的两个数字之积为正数则润泽赢，问：天一赢的概率是 ．13. 掷一枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数，则这枚骰子向上的一面的点数是2的整数倍的概率为 ．14. 一个袋中有3个白球和2个红球，它们除颜色不同外都相同．任意摸出一个球后放回，再任意摸出一球，则两次都摸到红球的概率为 ．15. 在一个不透明的袋子里放有黑，白各两个小球，它们只有颜色上的区别，从袋子中随机摸出一个小球记下颜色后不放回，再随机摸一个，则摸出两个小球为同一颜色概率是 ．
三、解答题
-
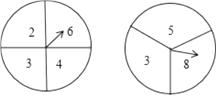
16. 初三年（4）班要举行一场毕业联欢会，主持人同时转动下图中的两个转盘，由一名同学在转动前来判断两个转盘上指针所指的两个数字之和是奇数还是偶数，如果判断错误，他就要为大家表演一个节目；如果判断正确，他可以指派别人替自己表演节目．现在轮到小明来选择，小明不想自己表演，于是他选择了偶数．
小明的选择合理吗？从概率的角度进行分析（要求用树状图或列表方法求解）
17. 在一个不透明的口袋中有1个红球，1个绿球和1个白球，这3个球除颜色不同外，其他都相同．从口袋中随机摸出1个球，记录其颜色，然后放回口袋并摇匀；再从口袋中随机摸出1个球，记录其颜色．请用画树状图（或列表）的方法，求两次摸到的球颜色不同的概率．18. 小颖和小丽做“摸球”游戏：在一个不透明的袋子中装有编号为1－4的四个球（除编号不同外其它都相同），从中随机摸出一个球，记下数字后放回，再从中摸出一个球，记下数字．若两次数字之和大于5，则小颖胜，否则小丽胜．这个游戏对双方公平吗？请说明理由．19. 现有九张背面一模一样的扑克牌，正面分别为：红桃A、红桃2、红桃3、红桃4、黑桃A、黑桃2、黑桃3、黑桃4、黑桃5．
（1）现将这九张扑克牌混合均匀后背面朝上放置，若从中摸出一张，求正面写有数字3的概率是多少？
（2）现将这九张扑克牌分成红桃和黑桃两部分后背面朝上放置，并将红桃正面数字记作m，黑桃正面数字记作n，若从黑桃和红桃中各任意摸一张，求关于x的方程mx2+3x+=0有实根的概率．（用列表法或画树形图法解，A代表数字1）20.如图，用红、蓝两种颜色随机地对A、B、C三个区域分别进行涂色，每个区域必须涂色并且只能涂一种颜色，请用列举法（画树状图或列表）求A、C两个区域所涂颜色不相同的概率．
21. 将分别标有数字1、2、3的三张卡片洗匀后，背面朝上放在桌面上．
（1）若随机地抽取一张，则抽到数字恰好为1的概率是 ；
（2）请你通过列表或画树状图分析：先随机地抽取一张作为十位上的数字（不放回），再抽取一张作为个位上的数字，求组成的两位数能被4整除的概率.22. 甲口袋里装有2个相同的小球，它们分别写有数字1和2；乙口袋里装有3个相同的小球，它们分别写有数字3，4，5；丙口袋里有2个相同的小球，它们分别写有数字6，7。从三个口袋中各随机地取出1个小球，按要求解答下列问题：
（1）画出“树形图”；
（2）取出的3个小球上只有1个偶数数字的概率是多少？
（3）取出的3个小球上全是奇数数字的概率是多少？
23.端午节吃粽子是中华民族的传统习俗，一超市为了吸引消费者，增加销售量特设计了一个游戏，其规则是：分别转动如图所示的两个可以自由转动的转盘各一次，每次指针落在每一字母区域的机会均等（若指针恰好落在分界线上重转），当两个转盘的指针所指字母都相同时，消费者就可以获得一次八折优惠价购买粽子的机会.
（1）用树状图或列表的方法（只选其中一种）表示出游戏可能出现的所有结果.
（2）若一名消费者只能参加一次游戏，则他能获得八折优惠价购买粽子的概率是多少？