（鲁教版）2022-2023学年九年级数学下册5.7切线长定理同步测试
试卷更新日期：2022-10-26 类型：同步测试
一、单选题
-
1. 如图，PA，PB分别与⊙O相切于A、B两点．直线EF切⊙O于C点，分别交PA、PB于E、F，且PA＝10．则△PEF的周长为（ ）
A、10 B、15 C、20 D、252. 如图，AB是⊙O的直径，点C为⊙O外一点，CA、CD是⊙O的切线，A、D为切点，连接BD、AD ． 若∠ACD＝48°，则∠DBA的大小是（ ）
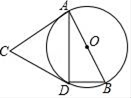A、32° B、48° C、60° D、66°3. 如图，PA切☉O于A，PB切☉O于B，连结OP，AB.下列结论不一定正确的是（ ）
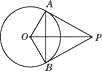A、PA=PB B、OP垂直平分AB C、∠OPA=∠OPB D、PA=AB4. 如图，从圆O外一点P引圆O的两条切线PA，PB，切点分别为A，B.如果∠APB=60°，PA=8，那么弦AB的长是（ ）
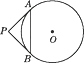A、4 B、8 C、 D、5. 下列说法正确的是（ ）A、过任意一点总可以作圆的两条切线 B、圆的切线长就是圆的切线的长度 C、过圆外一点所画的圆的两条切线长相等 D、过圆外一点所画的圆的切线长一定大于圆的半径6. 如图，PA，PB切⊙O于A，B两点，CD切⊙O于点E，交PA，PB于C，D．若⊙O的半径为1，△PCD的周长等于2 ，则线段AB的长是（ ）
A、 B、3 C、2 D、37. 如图，PA，PB，CD与⊙O相切于点为A，B，E，若PA=7，则△PCD的周长为（ ）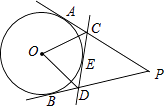
A、7 B、14 C、10.5 D、108. 已知如图，PA、PB切⊙O于A，B，MN切⊙O于C，交PB于N；若PA=7.5cm，则△PMN的周长是（ ）
A、7.5cm B、10cm C、15cm D、12.5cm9. 如图，四边形ABCD中，AD平行BC，∠ABC=90°，AD=2，AB=6，以AB为直径的半⊙O 切CD于点E，F为弧BE上一动点，过F点的直线MN为半⊙O的切线，MN交BC于M，交CD于N，则△MCN的周长为（ ）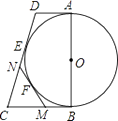
A、9 B、10 C、3 D、2
10. 如图，△ABC是一张周长为17cm的三角形的纸片，BC=5cm，⊙O是它的内切圆，小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN，则剪下的三角形的周长为（ ）
A、12cm B、7cm C、6cm D、随直线MN的变化而变化二、填空题
-
11. 如图，AB为半圆的直径，C是半圆弧上一点，正方形DEFG的一边DG在直径AB上，另一边DE过△ABC的内切圆圆心O，且点E在半圆弧上．若正方形DEFG的面积为100，且△ABC的内切圆半径r=4，则半圆的直径AB= ．
12. 由⊙O外一点F作⊙O的两条切线，切点分别为B、D，AB是⊙O的直径，连接AD、BD，线段OF交⊙O于E，交BD于C，连接DE、BE．有下列序号为①～④的四个结论：①BE=DE；②∠EBD=∠EDB；③DE∥AB；④BD2=2AD•FC其中正确的结论有 ． （把你认为正确结论的序号全部填上）
13. 如图，已知圆O内切于五边形ABCDE，切点分别是M、N、P、Q、R，且AB=5，BC=7，CD=8，DE=9，EA=4，则 的值是 ．
14. 如图，已知ABCD是一个半径为R的圆内接四边形，AB=12，CD=6，分别延长AB和DC，它们相交于点P，且BP=8，∠APD=60°，则R= ．
15. 如图，四边形ABCD是正方形，以BC边为直径在正方形内作半圆O，再过顶点A作半圆O的切线（切点为F）交CD边于E，则sin∠DAE= ．
三、解答题
-
16. 已知⊙O中，AC为直径，MA、MB分别切⊙O于点A、B．
（Ⅰ）如图①，若∠BAC=25°，求∠AMB的大小；
（Ⅱ）如图②，过点B作BD⊥AC于点E，交⊙O于点D，若BD=MA，求∠AMB的大小．
17. 如图， 和 是⊙ 的两条切线，A，B是切点．C是 上任意一点，过点C画⊙ 的切线，分别交 和 于D，E两点，已知 ，求 的周长．
18. 如图， ， 分别与 相切于 两点，若 ，求 的度数．
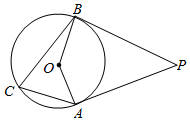19. 如图，PA、PB是⊙O的两条切线，A、B是切点，AC是⊙O的直径，∠BAC＝35°，求∠P的度数．
20. 如图， ， 分别与⊙O相切于 ， 两点，点 在⊙O上，已知 ，求 的度数．
