（鲁教版）2022-2023学年九年级数学下册5.6直线和圆的位置关系同步测试
试卷更新日期：2022-10-26 类型：同步测试
一、单选题
-
1. 点P是半径为10的圆O所在平面上的一点，且点P到点O的距离为8.则过点P的直线l与圆O的位置关系为（ ）A、相交 B、相切 C、相离 D、相交、相切、相离都有可能2. 如图，∠O=30°，C为OB上一点，且OC=6，以点C为圆心，半径为3的圆与OA的位置关系是（ ）A、相离 B、相交 C、相切 D、以上三种情况均有可能3. 已知在平面直角坐标系中，圆P的圆心坐标为（4，5），半径为3个单位长度，把圆P沿水平方向向左平移d个单位长度后恰好与y轴相切，则d的值是（ ）A、1 B、2 C、2或8 D、1或74. 以坐标原点O为圆心，作半径为2的圆，若直线y=﹣x+b与⊙O相交，则b的取值范围是（ ）A、0≤b＜2
B、﹣2 
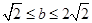C、﹣2 
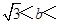2 
D、﹣2 ＜b＜2
5. 在Rt△ABC中，∠C=90°，AC=3，BC=4．若以1为半径的圆在△ABC所在平面上运动，则这个圆与△ABC的三条边的公共点最多有（ ）A、2个 B、3个 C、4个 D、5个6. OA平分∠BOC，P是OA上任一点（O除外），若以P为圆心的⊙P与OC相离，那么⊙P与OB的位置关系是（ ）
A、相离 B、相切 C、相交 D、相交或相切7. 在平面直角坐标系中，以点(-3，4)为圆心，4为半径的圆（ ）A、与x轴相交，与y轴相切 B、与x轴相离，与y轴相交 C、与x轴相切，与y轴相离 D、与x轴相切，与y轴相交8. 已知直线l与半径为r的☉O相交，且点O到直线l的距离为6，则r的取值范围是（ ）A、r<6 B、r=6 C、r>6 D、r≥69. 如图，☉O的圆心O到直线l的距离为3 cm，☉O的半径为1 cm，将直线l向右(垂直于l的方向)平移，使l与☉O相切，则平移的距离为（ ）
A、1 cm B、2 cm C、4 cm D、2 cm或4 cm10. 如果圆的最大弦长是m，直线与圆心的距离为d，且直线与圆相离，那么（ ）A、d＞m B、d＞ m C、d≥ m D、d≤ m二、填空题
-
11. 在Rt△ABC中，∠C=90°，AC=3，BC=4．若以C点为圆心，r为半径所作的圆与斜边AB只有一个公共点，则r的取值范围是 ．12. 如图所示，在直角坐标系中，⊙M的圆心坐标为（m，0），半径为2，如果⊙M与y轴所在直线相切，那么m= ， 如果⊙M与y轴所在直线相交，那么m的取值范围是 ．
13. 如图，△ABC中，AB=AC=5cm，BC=8cm，以A为圆心，3cm长为半径的圆与直线BC的位置关系是 ．
14. 若直线a与⊙O交于A，B两点，O到直线a的距离为6，AB=16，则⊙O的半径为 ．
15. 设☉O的半径为R，圆心O到直线l的距离为d，若d，R是方程x2-6x+m=0的两根，则直线l与☉O相切时，m的值为.
三、解答题
-
16. 如图所示，Rt△ABC中，∠ACB=90°，CA=6，CB=8，以C为圆心，r为半径作⊙C，当r为多少时，⊙C与AB相切？
17.如图，平行四边ABCD中，O为AB上的一点，连接OD.OC，以O为圆心，OB为半径画圆，分别交OD，OC于点P，Q．若OB=4，OD=6，∠ADO=∠A，
=2π，判断直线DC与⊙O的位置关系，并说明理由．
18.如图，AB是⊙O的直径，弦CD⊥AB于H．点G在⊙O上，过点G作直线EF，交CD延长线于点E，交AB的延长线于点F．连接AG交CD于K，且KE＝GE．
（1）判断直线EF与⊙O的位置关系，并说明理由；
（2）若AC∥EF，= ， FB＝1，求⊙O的半径．19.如图，点A，B，C，D在⊙O上，AB=AC，AD与BC相交于点E，AE=ED，延长DB到点F，使DB到点F，使FB=BD，连接AF.
⑴△BDE∽△FDA；
⑵试判断直线AF与⊙O的位置关系，并给出证明。20.如图：已知在正方形ABCD中，E是边AB的中点，点F在BC上，且∠ADE＝∠FDE。
(1)求证：DF＝AB＋FB；
(2)以E为圆心EB为半径作⊙E，试判断⊙E与直线DF的位置关系，并说明理由；
(3)在⑵的条件下，若CD=4cm，点M在线段DF上从点D出发向点F运动，速度为0.5cm/s，以M为圆心，MD为半径作⊙M。当运动时间为多少秒时，⊙M与⊙E相切？21.在坐标平面内，半径为R的⊙C与x轴交于点D（1，0）、E（5，0），与y轴的正半轴相切于点A。点A、B关于x轴对称，点P（a，0）在x的正半轴上运动，作直线BP，作EH⊥BP于H。
⑴求圆心C的坐标及半径R的值；
⑵△POB和△PHE随点P的运动而变化，若它们全等，求a的值；
⑶当a＝6时，试确定直线BP与⊙C的位置关系并说明理由。
