（鲁教版）2022-2023学年九年级数学下册5.5确定圆的条件同步测试

试卷更新日期：2022-10-26 类型：同步测试

进入出卷网下载

一、单选题

1. 下列命题正确的是（）

A、两点之间，直线最短 B、正六边形的外角和大于正五边形的外角和 C、不在同一条直线上的三个点确定一个圆 D、一个图形和它经过平移所得到的图形中，对应线段平行且相等

查看试题解析
2. 如图的矩形ABCD中，E为 $\bar{A B}$ 的中点，有一圆过C、D、E三点，且此圆分别与 $\bar{A D}$ 、 $\bar{B C}$ 相交于P、Q两点．甲、乙两人想找到此圆的圆心O，其作法如下：
（甲）作∠DEC的角平分线L，作 $\bar{D E}$ 的中垂线，交L于O点，则O即为所求；
（乙）连接 $\bar{P C}$ 、 $\bar{Q D}$ ，两线段交于一点O，则O即为所求
对于甲、乙两人的作法，下列判断何者正确？（）

A、两人皆正确 B、两人皆错误 C、甲正确，乙错误 D、甲错误，乙正确

查看试题解析
3. 下列说法中：
1）圆心角相等，所对的弦相等
2）过圆心的线段是直径
3）长度相等的弧是等弧
4）弧是半圆
5）三点确定一个圆
6）平分弦的直径垂直于弦，并且平分弦所对的弧
7）弦的垂直平分线必经过圆心
正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列四边形：①平行四边形；②矩形；③菱形；④正方形，其中四个顶点一定能在同一个圆上的有（）

A、①②③④ B、②③④ C、②④ D、③④

查看试题解析
5. 根据下列条件，A，B，C三点能确定一个圆的是（）

A、AB=2，BC=2，AC=4 B、AB=4.5，BC=5.5，AC=10 C、AB=4，BC=3，AC=5 D、AB= $\sqrt{2}$ ﹣1，BC= $\sqrt{2}$ +1，AC=2 $\sqrt{2}$

查看试题解析
6. 下列说法正确的是（）

A、过一点A的圆的圆心可以是平面上任意点 B、过两点A、B的圆的圆心在一条直线上 C、过三点A、B、C的圆的圆心有且只有一点 D、过四点A、B、C、D的圆不存在

查看试题解析
7.
小明不慎把家里的圆形镜子打碎了，其中四块碎片如图所示，为了配到与原来大小一样的圆形镜子，小明带到商店去的一块碎片应该是（　　）

A、第一块 B、第二块 C、第三块 D、第四块

查看试题解析
8.
如图，已知点平面直角坐标系内三点A（3，0）、B（5，0）、C（0，4），⊙P经过点A、B、C，则点P的坐标为（　　）

A、（6，8） B、（4，5） C、（4， $\frac{31}{8}$ ） D、（4， $\frac{33}{8}$ ）

查看试题解析
9. 可以作圆，且只可以作一个圆的条件是（）

A、已知圆心 B、已知半径 C、过三个已知点 D、过不在同一直线上的三点

查看试题解析
10.
如图，在5×5正方形网格中，一条圆弧经过A，B，C三点，那么这条圆弧所在圆的圆心是（）

A、点P B、点Q C、点R D、点M

查看试题解析

二、填空题

11. 如图，在四边形ADBC中，∠ACB=∠ADB=90°，AD=BD，AC=3，BC=4，则线段CD的长等于.

查看试题解析
12. 若A（1，2），B（3，﹣3），C（x，y）三点可以确定一个圆，则x、y需要满足的条件是．

查看试题解析
13. 如图所示，点A，B，C在同一直线上，点M在AC外，经过图中的三个点作圆，可以作个．

查看试题解析
14. 若A（1，2），B（3，﹣3），C（x，y）三点可以确定一个圆，则x、y需要满足的条件是．

查看试题解析
15. 下列说法：①直径是弦；②经过三点一定可以作圆；③三角形的外心到三角形各顶点的距离相等；④长度相等的弧是等弧；⑤平分弦的直径垂直于弦．其中正确的是（填序号）．

查看试题解析

三、解答题

16. 在△ABC中，CE，BD分别是边AB，AC上的高，F是BC边上的中点．

(1)、指出图中的一个等腰三角形，并说明理由．

(2)、若∠A=x°，求∠EFD的度数（用含x的代数式表达）．

(3)、猜想∠ABC和∠EDA的数量关系，并证明．

查看试题解析
17. 已知直线l：y=x+4和点A（0，4），B（﹣4，0），设点C为直线l上一点，判断A，B，C是否在同一个圆上．

查看试题解析
18.
平面直角坐标系中，点A（2，9）、B（2，3）、C（3，2）、D（9，2）在⊙P上．
（1）在图中清晰标出点P的位置；
（2）点P的坐标是

查看试题解析
19.
操作与探究
我们知道：过任意一个三角形的三个顶点能作一个圆，探究过四边形四个顶点作圆的条件．
（1）分别测量图1、2、3各四边形的内角，如果过某个四边形的四个顶点能一个圆，那么其相对的两个角之间有什么关系？证明你的发现．
（2）如果过某个四边形的四个顶点不能一个圆，那么其相对的两个角之间有上面的关系吗？试结合图4、5的两个图说明其中的道理．（提示：考虑∠B+∠D与180°之间的关系）
由上面的探究，试归纳出判定过四边形的四个顶点能作一个圆的条件．

查看试题解析
20. 求证：矩形的四个顶点在同一圆上.

查看试题解析

四、综合题

21. 如图，在平面直角坐标系中， $A (0 ， 4)$ 、 $B (4 ， 4)$ 、 $C (6 ， 2)$ ．

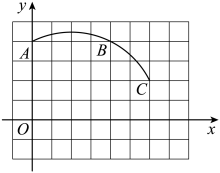(1)、在图中画出经过A、B、C三点的圆弧所在圆的圆心M的位置．

(2)、写出圆心点M的坐标为；

(3)、若 $D M = 2 \sqrt{5}$ ，判断点D与 $⊙ M$ 的位置关系．

查看试题解析
22.

(1)、【问题提出】如图1，在 $△ A B C$ 中， $∠ C = 90 °$ ， $B D$ 平分 $∠ A B C$ 交 $A C$ 于点D，设 $C D$ 的长为m，点D到边 $A B$ 的距离为n，则mn；（填“＞”“＜”或“＝”）

(2)、【问题探究】
如图2，在梯形 $A B C D$ 中， $∠ A = 90 °$ ， $A D ∥ B C$ ， $A B = 20 (1 + \sqrt{2})$ ， $B D$ 为对角线，且 $∠ B D C = 45 °$ ，求 $△ B C D$ 面积的最小值；

(3)、【问题解决】
某景点有一个形状为菱形 $A B C D$ 的草坪，如图3， $A B = 40 \sqrt{3}$ 米， $∠ B = 60 °$ ，现欲将该草坪扩建为 $△ B E F$ ，使得点E、F分别在 $B A$ 、 $B C$ 的延长线上，且边 $E F$ 经过点D，为了节省成本，要求扩建后的草坪面积（ $△ B E F$ 的面积）尽可能小，问 $△ B E F$ 的面积是否存在最小值？若存在，求出其最小值；若不存在，请说明理由.

查看试题解析
23. 在△ABC中，AC＝BC＝5，tanA＝ $\frac{3}{4}$ ， E分别是AB，AC边上的动点，作△ADE关于DE对称的图形△A′DE.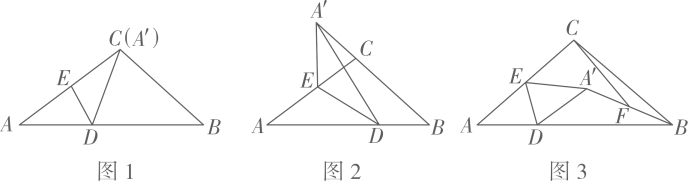

(1)、如图1，当点A′恰好与点C重合，求DE的长；

(2)、如图2，当点A’落在BC的延长线上，且A’E⊥AB，求AD的长；

(3)、如图3，若AE=CE，连接A’B，F是A’B的中点，连接CF，在D点的运动过程中，求线段CF长度的最大值.

查看试题解析