（鲁教版）2022-2023学年九年级数学下册5.3垂径定理 同步测试
试卷更新日期：2022-10-26 类型：同步测试
一、单选题
-
1. 如图，在⊙O中AB为直径，C为弧AB的中点，EF∥AB，连接AC交EF于点D，若已知DF＝2DE，则CD：AD的值为（ ）
A、1：3 B、1：2 C、1：2 D、1：42. 若弦AB，CD是⊙O的两条平行弦，⊙O的半径为13，AB=10，CD=24，则AB，CD之间的距离为（ ）A、7 B、17 C、5或12 D、7或173. 如图，△ABC内接于⊙O，OD⊥AB于D，OE⊥AC于E，连结DE．且DE＝ ，则弦BC的长为（ ）
A、 B、2 C、3 D、4. 如图，线段AB是⊙O的直径，弦CD⊥AB，∠CAB=30°，OD=2，那么DC的长等于（ ）
A、2 B、4 C、 D、5. 为了测量一个铁球的直径，将该铁球放入工件槽内，测得的有关数据如图所示（单位：cm），则该铁球的直径为（ ）
A、12cm B、10cm C、8cm D、6cm6. 如图，△ABC为⊙O的内接等边三角形，BC=12，点D为 上一动点，BE⊥OD于E，当点D由点B沿 运动到点C时，线段AE的最大值是（ ）
A、 B、2 C、6 D、7. 在半径为2R的圆中，垂直平分半径的弦长等于（ ）.A、 B、 C、 D、 R8. 如图，在半径为6cm的⊙O中，点A是劣弧BC的中点，点D是优弧BC上一点，且∠D＝30°，下列四个结论：①OA⊥BC；②BC＝6 cm；③sin∠AOB＝ ；④四边形ABOC是菱形．其中正确结论的序号是（ ）
A、①③ B、①②③④ C、②③④ D、①③④9. 如图，EF是⊙O的直径，点P在EF的延长线上，点B、D在⊙O上，连结PB、PD分别交⊙O于点A，C，已知∠BPO=∠DPO，则下列说法中不一定正确的是（ ）
A、AB=CD B、EF⊥BD C、
D、 . 
10. 如图，AB是⊙O的直径，弦CD交AB于点P，AP=2，BP=6，∠APC=30°，则CD的长为（ ）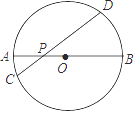
A、 B、2 C、2 D、8二、填空题
-
11. ⊙O的半径为10，弦AB//CD，AB=12，CD=16，则AB与CD之间的距离为 ．12. 如图是一个高速公路隧道的横截面，若它的形状是以O为圆心的圆的一部分，路面AB=8米，净高CD=8米，则此圆的半径OA为.
13. 如图，AB是⊙的直径，点C是半径OA的中点，过点C作 ，交O于点D、E两点，过点D作直径DF，连结AF，则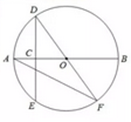
14. 如图，△ABC内接于⊙O，AO＝2，BC＝ ，则∠BAC的度数为°.
15. 如图，在矩形 中， ， ，E为 边上一动点，F、G为 边上两个动点，且 ，则线段 的长度最大值为.
三、解答题
-
16. 已知：如图，AB是⊙O的弦，半径OC、OD分别交AB于点E、F，且OE=OF．求证：AE=BF．
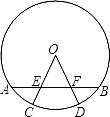17. 如图为桥洞的形状，其正视图是由 和矩形ABCD构成．O点为 所在⊙O的圆心，点O又恰好在AB为水面处．若桥洞跨度CD为8米，拱高（OE⊥弦CD于点F）EF为2米．求 所在⊙O的半径DO．
18. 如图，在同一平面内，有一组平行线l1、l2、l3 ， 相邻两条平行线之间的距离均为4，点O在直线l1上，⊙O与直线l3的交点为A、B，AB=12，求⊙O的半径．
19. 如图，AB是⊙O的弦，点C、D在弦AB上，且AD=BC，联结OC、OD．求证：△OCD是等腰三角形．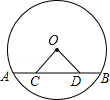
20. 如图，∠C=90°，以AC为半径的圆C与AB相交于点D．若AC=3，CB=4，求BD长．
