（鲁教版）2022-2023学年九年级数学下册5.2 圆的对称性 同步测试
试卷更新日期：2022-10-26 类型：同步测试
一、单选题
-
1. 如图，四边形ABCD内接于⊙O，AC平分∠BAD，则下列结论正确的是（ ）
A、AB=AD B、BC=CD C、 D、∠BCA=∠DCA2. 如图所示，在⊙O中， ，∠A=30°，则∠B=（ ）
A、150° B、75° C、60° D、15°3. 如图，弧AD是以等边三角形ABC一边AB为半径的四分之一圆周，P为弧AD上任意一点，若AC=5，则四边形ACBP周长的最大值是（ ）
A、15 B、15+5 C、20 D、15+54. 下列说法中，正确的是（ ）
A、等弦所对的弧相等 B、等弧所对的弦相等 C、圆心角相等，所对的弦相等 D、弦相等所对的圆心角相等5. 过圆内一点可以做圆的最长弦（ ）A、1条 B、2条 C、3条 D、4条6. 如图，在Rt△ABC中，∠ACB=90°，∠A=56°．以BC为直径的⊙O交AB于点D．E是⊙O上一点，且 = ，连接OE．过点E作EF⊥OE，交AC的延长线于点F，则∠F的度数为（ ）
A、92° B、108° C、112° D、124°7. 把一张圆纸片按如图所示方式折叠两次后展开，图中的虚线表示折痕，则弧AB的度数是（ ）
A、120° B、135° C、150° D、165°8. 如图，AB是⊙O的弦，OA、OC是⊙O的半径，弧AC=弧BC，∠BAO=37 ，则∠AOC的度数是（ ）度
A、74 B、106 C、117 D、1279. 如图，A，B，C，D是⊙O上的四个点，AD∥BC．那么 与 的数量关系是（ ）
A、 = B、 ＞ C、 ＜ D、无法确定10. 如图，在⊙O中 = ，∠AOB=40°，则∠COD的度数（ ）
A、20° B、40° C、50° D、60°二、填空题
-
11. 下列命题①不相交的直线是平行线；②矩形的对角线相等且互相平分；③同位角相等；④平行四边形既是中心对称图形又是轴对称图形；⑤同圆中同弦所对的圆周角相等.其中正确的序号是.12. 如图，四边形 内接于 ， 是 的直径， ， 与 相交于点 ，若 ，则 .
13. 如图，AB是⊙O的直径，BC是弦，点E是 的中点，OE交BC于点D．连接AC，若BC=6，DE=1，则AC的长为 ．
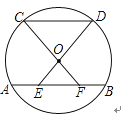
14. 如图，P（x，y）是以坐标原点为圆心、5为半径的圆周上的点，若x、y都是整数，则这样的点共有个．
15. 如图，在⊙O中， = ，AB=2，则AC= ．
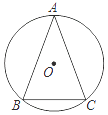
三、解答题
-
16. 如图，以□ABCD的顶点A为圆心，AB为半径作⊙A，分别交BC，AD于E，F两点，交BA的延长线于G，判断 和 是否相等，并说明理由．
17.如图所示，已知F是以O为圆心，BC为直径的半圆上任一点，A是弧BF的中点，AD⊥BC于点D，求证：AD= BF．
18.如图，已知AB是⊙O的直径，M，N分别是AO，BO的中点，CM⊥AB，DN⊥AB．求证： ．
19. 已知：如图，在圆O中，弦AB，CD交于点E，AE=CE．求证：AB=CD．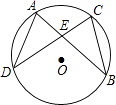
20.作图题：在⊙O 中，点D是劣弧AB的中点，仅用无刻度的直尺画线的方法，按要求完下列作图：
在图（1）中作出∠C的平分线；在图（2）中画一条弦，平分△ABC的面积．
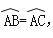， ∠ACB=60°，求证：∠AOB=∠BOC=∠AOC．
的三等分点，AB分别交OC、OD于点E、F，求证：AE=CD．
