(北师大版)2022-2023学年度第一学期九年级数学6.3反比例函数的应用 同步测试
试卷更新日期:2022-10-26 类型:同步测试
一、单选题
-
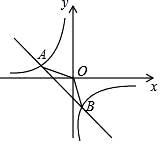
1. 已知正比例函数的图象与反比例函数的图象交于点 , , 则点的坐标是( )A、 B、 C、 D、2. 如图,已知点 , , 是轴上位于点上方的一点,平分 , 平分 , 直线交于点 . 若反比例函数的图像经过点 , 则的值是( )
 A、-8 B、-9 C、-10 D、-123. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A、-8 B、-9 C、-10 D、-123. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )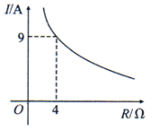 A、函数解析式为 B、蓄电池的电压是18V C、当时, D、当时,4. 如果反比例函数图象经过点A(-1,2),那么此反比例函数解析式为( )A、 B、 C、 D、5. 点在反比例函的图象上,则下列说法正确的是( )A、 B、函数的图象关于对称 C、函数的图象经过点(6,1) D、函数的图象关于原点对称6. 反比例函数经过点 , 则下列说法不正确的是( )A、 B、函数图象分布在第一、三象限 C、当时,随的增大而增大 D、当时,随的增大而减小7. 如图,直线与x轴交于点B,双曲线(x>0)交于点A,过点B作x轴的垂线,与双曲线交于点C,且AB=AC,则k的值为( )
A、函数解析式为 B、蓄电池的电压是18V C、当时, D、当时,4. 如果反比例函数图象经过点A(-1,2),那么此反比例函数解析式为( )A、 B、 C、 D、5. 点在反比例函的图象上,则下列说法正确的是( )A、 B、函数的图象关于对称 C、函数的图象经过点(6,1) D、函数的图象关于原点对称6. 反比例函数经过点 , 则下列说法不正确的是( )A、 B、函数图象分布在第一、三象限 C、当时,随的增大而增大 D、当时,随的增大而减小7. 如图,直线与x轴交于点B,双曲线(x>0)交于点A,过点B作x轴的垂线,与双曲线交于点C,且AB=AC,则k的值为( ) A、2 B、3 C、4 D、68. 已知反比例函数经过点A、B , 则m的值为( )A、-6 B、 C、 D、69. 如图所示,反比例函数 的图像经过点A(-2,a),B(-a+2,6),它与正比例函数 的图像交于点A,则下列结论正确的是( )
A、2 B、3 C、4 D、68. 已知反比例函数经过点A、B , 则m的值为( )A、-6 B、 C、 D、69. 如图所示,反比例函数 的图像经过点A(-2,a),B(-a+2,6),它与正比例函数 的图像交于点A,则下列结论正确的是( ) A、 B、 C、 D、反比例函数 与正比例函数 ,都随x的增大而减小10. 如图,菱形OABC的顶点B在y轴上,顶点C的坐标为(-3,2).若反比例函数y= (x>0)的图象经过点A,则k的值为( )
A、 B、 C、 D、反比例函数 与正比例函数 ,都随x的增大而减小10. 如图,菱形OABC的顶点B在y轴上,顶点C的坐标为(-3,2).若反比例函数y= (x>0)的图象经过点A,则k的值为( ) A、-6 B、-3 C、3 D、6
A、-6 B、-3 C、3 D、6二、填空题
-
11. 如图,在平面直角坐标系中,已知第一象限上的点A(m,n)是双曲线上的动点,过点A作AM∥y轴交x轴于点M,过点N(0,2n)作NB∥x轴交双曲线于点B,交直线AM于点C,若四边形OACB的面积为4,则k的值为 .
 12. 如图,等边△ABO的顶点O与原点重合,点A的坐标是(-4,0),点B在第二象限.反比例函数的图象经过点B,则k的值是 .
12. 如图,等边△ABO的顶点O与原点重合,点A的坐标是(-4,0),点B在第二象限.反比例函数的图象经过点B,则k的值是 .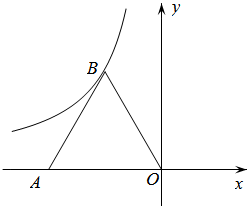 13. 如图,将Rt△ABO放置在直角坐标系中,OB边与x轴重合,AO=10, , 反比例函数(x<0)的图象经过AO的中点C,且与AB交于点D,则BD的长为 .
13. 如图,将Rt△ABO放置在直角坐标系中,OB边与x轴重合,AO=10, , 反比例函数(x<0)的图象经过AO的中点C,且与AB交于点D,则BD的长为 .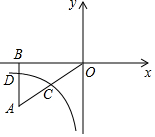 14. 如图,点A、B分别在x轴的正半轴和负半轴上,以AB为边在x轴的上方作正方形ABCD,正方形ABCD对角线的交点坐标为I(a,b),在正方形ABCD的内部作正方形OPMN,使得O、P、M、N分别落在AB、BC、CD、DA上,若双曲线经过点N和点I,则的值是 .
14. 如图,点A、B分别在x轴的正半轴和负半轴上,以AB为边在x轴的上方作正方形ABCD,正方形ABCD对角线的交点坐标为I(a,b),在正方形ABCD的内部作正方形OPMN,使得O、P、M、N分别落在AB、BC、CD、DA上,若双曲线经过点N和点I,则的值是 . 15. 一辆汽车前灯电路上的电压U(V)保持不变,选用灯泡的电阻为R(Ω),通过的电流强度为I(A),由欧姆定律可知,I . 当电阻为40Ω时,测得通过的电流强度为0.3A.为保证电流强度不低于0.2A且不超过0.6A,则选用灯泡电阻R的取值范围是 .
15. 一辆汽车前灯电路上的电压U(V)保持不变,选用灯泡的电阻为R(Ω),通过的电流强度为I(A),由欧姆定律可知,I . 当电阻为40Ω时,测得通过的电流强度为0.3A.为保证电流强度不低于0.2A且不超过0.6A,则选用灯泡电阻R的取值范围是 .三、解答题
-
16. 已知与x成反比例,当时, , 求y与x的函数表达式.17. 已知反比例函数 和一次函数 的图象只有一个公共点,求 的值.18. 已知反比例函数y= (k≠0)的图象经过点(﹣2,8).求这个反比例函数的解析式.19. 在平面直角坐标系 中,直线 与反比例函数 图象的一个交点为 ,求k的值.20. 如图,Rt△ABO的顶点A是双曲线 与直线y=−x−(k+1)在第二象限的交点,AB⊥x轴于B且S△ABO= 。
 (1)、求这两个函数的解析式。(2)、求直线与双曲线的两个交点A,C的坐标和△AOC的面积。21. 如图,在平面直角坐标系xOy中,反比例函数y= 的图象与一次函数y=-x+1的图象的一个交点为A(-1,m).
(1)、求这两个函数的解析式。(2)、求直线与双曲线的两个交点A,C的坐标和△AOC的面积。21. 如图,在平面直角坐标系xOy中,反比例函数y= 的图象与一次函数y=-x+1的图象的一个交点为A(-1,m). (1)、求这个反比例函数的表达式;(2)、如果一次函数y=-x+1的图象与x轴交于点B(n,0),请确定当x<n时,对应的反比例函数y= 的值的范围.
(1)、求这个反比例函数的表达式;(2)、如果一次函数y=-x+1的图象与x轴交于点B(n,0),请确定当x<n时,对应的反比例函数y= 的值的范围.