(鲁教版)2022-2023学年度第一学期八年级数学5.3三角形的中位线 同步测试
试卷更新日期:2022-10-26 类型:同步测试
一、单选题
-
1. 如图,三角形纸片ABC,点D是BC边上一点,连结AD,把 沿着AD翻折,得到 ,DE与AC交于点F.若点F是DE的中点, , , 的面积为9,则点F到BC的距离为( )
 A、1.4 B、2.4 C、3.6 D、4.82. 如图,在中, , 点D,E,F分别是三边的中点,且 , 则的长度是( )
A、1.4 B、2.4 C、3.6 D、4.82. 如图,在中, , 点D,E,F分别是三边的中点,且 , 则的长度是( ) A、 B、 C、 D、3. 如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P.若BC=10,则PQ的长为( )
A、 B、 C、 D、3. 如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P.若BC=10,则PQ的长为( ) A、 B、 C、3 D、44. 如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°, , 则下列结论:①∠CAD=30° ② ③S平行四边形ABCD=AB•AC ④ ,正确的个数是( )
A、 B、 C、3 D、44. 如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°, , 则下列结论:①∠CAD=30° ② ③S平行四边形ABCD=AB•AC ④ ,正确的个数是( )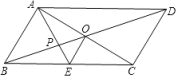 A、1 B、2 C、3 D、45. 如图,一次函数 的图象分别与x轴、y轴交于 两点,过原点O作 垂直于直线 交 于点 ,过点 作 垂直于x轴于点 ,过点 作 垂直于直线 交 于点 ,过点 过点作 垂直于x轴于点 ……依此规律作下去,则点 的坐标是( )
A、1 B、2 C、3 D、45. 如图,一次函数 的图象分别与x轴、y轴交于 两点,过原点O作 垂直于直线 交 于点 ,过点 作 垂直于x轴于点 ,过点 作 垂直于直线 交 于点 ,过点 过点作 垂直于x轴于点 ……依此规律作下去,则点 的坐标是( )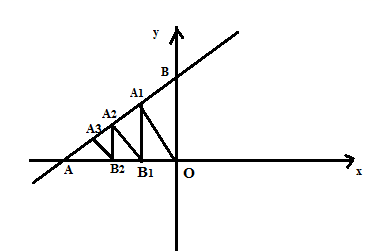 A、 B、 C、 D、6. 如图,四边形ABCD中,∠ABC=120°,点F为CD中点,以AB,BD为边,AD为对角线作平行四边形ABDE,连接BE交AD于点O,且OF=BC=2,则AB的长为( )
A、 B、 C、 D、6. 如图,四边形ABCD中,∠ABC=120°,点F为CD中点,以AB,BD为边,AD为对角线作平行四边形ABDE,连接BE交AD于点O,且OF=BC=2,则AB的长为( ) A、 B、 C、 D、7. 如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于点G,CD=AE.若BD=6,CD=5,则△DCG的面积是( )
A、 B、 C、 D、7. 如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于点G,CD=AE.若BD=6,CD=5,则△DCG的面积是( ) A、10 B、5 C、 D、8. 如图,在 中, , ,直角 的顶点 是 的中点,两边 , 分别交 , 于点 , .现给出以下四个结论:① ;② 是等腰直角三角形;③ ;④ .当 在 内绕顶点 旋转时(点 不与点 , 重合),上述结论中始终正确的是( )
A、10 B、5 C、 D、8. 如图,在 中, , ,直角 的顶点 是 的中点,两边 , 分别交 , 于点 , .现给出以下四个结论:① ;② 是等腰直角三角形;③ ;④ .当 在 内绕顶点 旋转时(点 不与点 , 重合),上述结论中始终正确的是( ) A、①②③ B、①②④ C、②③④ D、①③④9. 如图,在 中, , , ,D、E分别是 、 的中点,则 的长为( )
A、①②③ B、①②④ C、②③④ D、①③④9. 如图,在 中, , , ,D、E分别是 、 的中点,则 的长为( )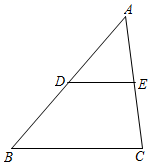 A、3 B、2.5 C、4 D、3.510. 如图,作边长为4的等边 ,延长 至点 ,使得 ,再以 为边作等边 .延长 至点 ,使得 =2 ,再以 为边作等边 ,以此类推…….若点 、 、 、 ……分别是 、 、 、 ……的中点,则 的长度为( )
A、3 B、2.5 C、4 D、3.510. 如图,作边长为4的等边 ,延长 至点 ,使得 ,再以 为边作等边 .延长 至点 ,使得 =2 ,再以 为边作等边 ,以此类推…….若点 、 、 、 ……分别是 、 、 、 ……的中点,则 的长度为( ) A、6058 B、6060 C、6062 D、6064
A、6058 B、6060 C、6062 D、6064二、填空题
-
11. 如图,在 中, , 是 的角平分线,E是 中点,连接 ,若 ,则 .
 12. 如图,平行四边形ABCD,对角线AC、BD相交于点O,点E是CD的中点, ,则AD的长是.
12. 如图,平行四边形ABCD,对角线AC、BD相交于点O,点E是CD的中点, ,则AD的长是. 13. 如图,在平面直角坐标系中,点B、C在y轴上,ΔABC是等边三角形,AB=4,AC与x轴的交点D的坐标是( , 0),则点A的坐标为.
13. 如图,在平面直角坐标系中,点B、C在y轴上,ΔABC是等边三角形,AB=4,AC与x轴的交点D的坐标是( , 0),则点A的坐标为.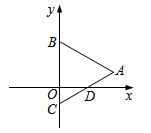 14. 如图,△ABC中,D、E分别是AB、AC的中点,若DE=4cm,则BC=cm.
14. 如图,△ABC中,D、E分别是AB、AC的中点,若DE=4cm,则BC=cm.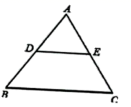 15. 如图,在△ABC中,∠ACB=90°,过点A作直线m∥BC,过AB的中点D作DE⊥CD,DE交直线m于点E,连结CE,已知BC=5,AC=12,则AE的长为.
15. 如图,在△ABC中,∠ACB=90°,过点A作直线m∥BC,过AB的中点D作DE⊥CD,DE交直线m于点E,连结CE,已知BC=5,AC=12,则AE的长为.
三、解答题
-
16. 如图,在中,D,E分别是边 , 的中点,连接 , . 若平分 , 求证: .
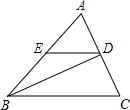 17. 如图,已知△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足是E,F是BC的中点,求证:BD=2EF.
17. 如图,已知△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足是E,F是BC的中点,求证:BD=2EF. 18. 如图,四边形 四条边上的中点分别为E、F、G、H,顺次连接 、 、 、 ,得到四边形 .求证:四边形 是平行四边形.
18. 如图,四边形 四条边上的中点分别为E、F、G、H,顺次连接 、 、 、 ,得到四边形 .求证:四边形 是平行四边形.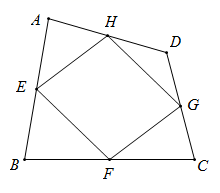 19. 如图已知Rt△ABC中,∠ACB=90°,∠B=15°,边AB的垂直平分线交边BC 于点E,垂足为点D,取线段BE的中点F,联结 DF,求证:AC=DF。
19. 如图已知Rt△ABC中,∠ACB=90°,∠B=15°,边AB的垂直平分线交边BC 于点E,垂足为点D,取线段BE的中点F,联结 DF,求证:AC=DF。 20. 如图, 和 中, ,连接 、 , 为 的中点,连接 . 求证: .
20. 如图, 和 中, ,连接 、 , 为 的中点,连接 . 求证: .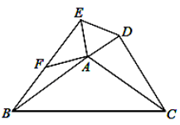 21. 如图,在△ABC中,D为BC边的中点,过D点分别作DE∥AB交AC于点E,DF∥AC交AB于点F.
21. 如图,在△ABC中,D为BC边的中点,过D点分别作DE∥AB交AC于点E,DF∥AC交AB于点F.求证:BF=DE.
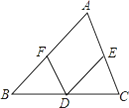 22. 如图,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=6,求线段DE的长.
22. 如图,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=6,求线段DE的长. 23. 操作与探究 探索:在如图1至图3中,△ABC的面积为a.
23. 操作与探究 探索:在如图1至图3中,△ABC的面积为a.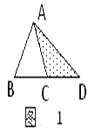

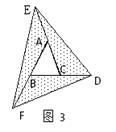

(1)、如图1,延长△ABC的边BC到点D,使CD=BC,连结DA.若△ACD的面积为S1 , 则S1=(用含a的代数式表示);
(2)、如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连结DE.若△DEC的面积为S2 , 则S2=(用含a的代数式表示);(3)、在图2的基础上延长AB到点F,使BF=AB,连结FD,FE,得到△DEF(如图3).若阴影部分的面积为S3 , 则S3=(用含a的代数式表示).发现:像上面那样,将△ABC各边均顺次延长一倍,连结所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的倍.