(鲁教版)2022-2023学年度第一学期八年级数学4.3中心对称 同步测试
试卷更新日期:2022-10-26 类型:同步测试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图形中,是中心对称图形,但不是轴对称图形的是( )A、
2. 下列图形中,是中心对称图形,但不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 下面的图形是用数学家名字命名的,其中是轴对称图形,但不是中心对称图形的是( )A、
3. 下面的图形是用数学家名字命名的,其中是轴对称图形,但不是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,-300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示错误的是( )
4. 在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,-300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示错误的是( ) A、 B、 C、 D、5. 下列命题是真命题的是( )A、若 ,则 为坐标原点 B、若 ,且 平行于x轴, ,则B点坐标为 C、点 关于原点对称的点坐标是 D、若关于一元一次不等式组 无解,则a的取值范围是6. 下列手机手势解锁图案中,属于中心对称图形的是( )A、
A、 B、 C、 D、5. 下列命题是真命题的是( )A、若 ,则 为坐标原点 B、若 ,且 平行于x轴, ,则B点坐标为 C、点 关于原点对称的点坐标是 D、若关于一元一次不等式组 无解,则a的取值范围是6. 下列手机手势解锁图案中,属于中心对称图形的是( )A、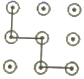 B、
B、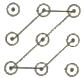 C、
C、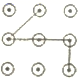 D、
D、 7. 图中的两个梯形成中心对称,点P的对称点是( )
7. 图中的两个梯形成中心对称,点P的对称点是( )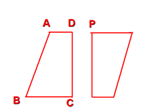 A、点A B、点B C、点C D、点D8. 若点 关于原点对称的点是点B,点B关于x轴对称的点是点C,则点C的坐标是( )A、 B、 C、 D、9. 在平面直角坐标系中,点 关于原点对称点在()A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 点M(1,-2)关于原点对称点的坐标为( )A、(2,-1) B、(-2,-1) C、(1,-2) D、(-1,2)
A、点A B、点B C、点C D、点D8. 若点 关于原点对称的点是点B,点B关于x轴对称的点是点C,则点C的坐标是( )A、 B、 C、 D、9. 在平面直角坐标系中,点 关于原点对称点在()A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 点M(1,-2)关于原点对称点的坐标为( )A、(2,-1) B、(-2,-1) C、(1,-2) D、(-1,2)二、填空题
-
11. 在平面直角坐标系中点M(2,﹣4)关于原点对称的点的坐标为 .12. 点 关于原点对称的点的坐标是.13. 如图,以正方形ABCD的中心O为原点建立平面直角坐标系,若点A的坐标为(-2,-2),则点 的坐标是 .
 14. 如图,点A,B在数轴上,它们对应的数分别为-2, , 且点A,B关于原点对称,则x的值是 .
14. 如图,点A,B在数轴上,它们对应的数分别为-2, , 且点A,B关于原点对称,则x的值是 .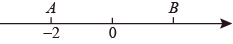 15. 在①平行四边形;②矩形;③菱形;④正方形;⑤等腰梯形这五种图形中,既是轴对称图形又是中心对称图形的是(只填序号).
15. 在①平行四边形;②矩形;③菱形;④正方形;⑤等腰梯形这五种图形中,既是轴对称图形又是中心对称图形的是(只填序号).三、解答题
-
16. △ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.
 (1)、作出△ABC关于原点O对称的△A1B1C1 , 并写出点C1的坐标;(2)、求△ABC的面积.17. 如果点 在第二象限,那么点 关于原点的对称点 在第几象限?18. 已知点M(2,a)在反比例函数y= (k≠0)的图象上,点M关于原点中心对称的点N在一次函数y=﹣2x+8的图象上,求此反比例函数的解析式.19. 已知点P(x,y)的坐标满足方程(x+3)2+ =0,求点P分别关于x轴,y轴以及原点的对称点坐标.20. 如图所示,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度)
(1)、作出△ABC关于原点O对称的△A1B1C1 , 并写出点C1的坐标;(2)、求△ABC的面积.17. 如果点 在第二象限,那么点 关于原点的对称点 在第几象限?18. 已知点M(2,a)在反比例函数y= (k≠0)的图象上,点M关于原点中心对称的点N在一次函数y=﹣2x+8的图象上,求此反比例函数的解析式.19. 已知点P(x,y)的坐标满足方程(x+3)2+ =0,求点P分别关于x轴,y轴以及原点的对称点坐标.20. 如图所示,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度)
①请画出△A1B1C1 , 使△A1B1C1与△ABC关于原点对称;
②将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2 , 并直接写出线段OB旋转到OB2扫过图形的面积.
21.如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(−2,−2),B(−4,−1),C(−4,−4).
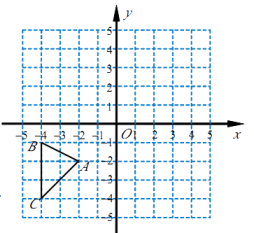 (1)、作出 ABC关于原点O成中心对称的 A1B1C1.(2)、作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在 A1B1C1的内部(不包括顶点和边界),求a的取值范围.22. 下面的两个题目中,请选择一个进行解答,多做不得分.
(1)、作出 ABC关于原点O成中心对称的 A1B1C1.(2)、作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在 A1B1C1的内部(不包括顶点和边界),求a的取值范围.22. 下面的两个题目中,请选择一个进行解答,多做不得分.题一
题二
请在平面直角坐标系中,完成下面的问题
⑴描出点A(-2,3)和它关于y轴的对称点B;
⑵描出点C(2,1)和它关于原点的对
称点D;
⑶求线段AD的长.
已知:如图,E、F是平行四边形ABCD对角线AC上的两点,且AE=CF.求证:BE=DF.
 23.
23.课外兴趣小组活动时,老师提出了如下问题:
 (1)、如图1,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
(1)、如图1,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
[感悟]解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(2)、解决问题:受到(1)的启发,请你证明下列命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.求证:BE+CF>EF,若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明.